快速成型中基于零件装配要求的分段分层算法

王春香，郝志博

(内蒙古科技大学机械学院，内蒙古 包头 014010)

1 基于STL模型分层算法的研究现状

STL模型的分层主要有：基于STL模型的等厚分层和基于STL模型的自适应分层。

现在对于STL模型的等厚分层主要有3种方法：①基于三角形面片几何特征的分层处理方法；②基于拓扑信息的分层处理方法；③基于STL模型的局部拓扑信息的分层处理方法。

基于三角形面片几何特征的分层处理方法是将三角形面片按照顶点坐标值将三角形面片进行分类分级排序求交，进而减少分层切平面与三角形面片求交的判断次数，提高分层效率；基于拓扑信息的分层处理方法首先对STL模型建立整体的拓扑信息，使散乱的三角形面片具有毗邻关系，当分层切平面与其中一个三角形面片相切时，便可以根据三角形面片之间的毗邻关系查找所有与其相切的三角形面片，直到与初次相切的三角形面片相交，完成一次求交过程，通过建立STL模型整体拓扑信息提高成功搜索三角形面片的效率，进而提高分层效率；基于STL模型的局部拓扑信息的分层处理方法是对上面两种方法的综合利用，首先对STL模型分组排序，然后动态建立局部的拓扑信息，该方法较大地提高了搜索三角形面片的效率，而且降低了内存使用率[1-6]。

STL模型等厚分层虽然能够快速分层，但由于阶梯误差的存在使得其在精度与效率两个方面很难协调。因此，许多学者提出了STL模型的自适应分层，用以使快速成型设备在提高效率的同时保证制造精度。

STL模型的自适应分层处理方法主要有3种：①基于面积法的自适应分层；②基于曲率的自适应分层；③基于法矢量的自适应分层。

基于面积法的自适应分层处理方法将相邻的两个层面的面积进行对比，根据面积比率值与给定值进行比较，当比值大于给定值时将下一层的层厚减小，当比值小于给定值时将下一层厚增大，这样依次循环直到模型顶端为止；基于曲率的自适应分层处理方法,根据当前层点的曲率与尖端高度之间的几何关系来确定当前的层厚；基于法矢量的自适应分层处理方法，由于STL文件不仅储存三角形面片的三个顶点坐标信息而且储存每一个三角形面片的法矢量信息，故分层厚度值可依据三角形面片法矢量与分层方向的夹角和尖端高度值之间的关系来确定[7-9]。

2 分层算法的改进

等厚分层是按照一定厚度对模型进行分层，自适应分层是按照一定条件进行等精度的分层，等厚分层算法虽然可以提高分层效率，但是当STL模型形状变化复杂时会造成明显的阶梯效应；而自适应分层算法的提出较大地减轻了阶梯效应，但是不能满足模型各部位功能装配要求。如果模型的不同部位要求的精度不同时，这两种方法只能按照精度较高的部位对模型进行整体分层或者是将模型进行分部位加工最后再进行黏合加工，造成加工效率的大幅降低；当模型存在尖端部位时，无论是等厚分层还是自适应分层如果加大分层厚度会导致该尖端部位的丢失，如果减小分层厚度会导致零件制造时间大幅度增加。本文基于这种情况，提出一种分段分层算法：按照不同精度要求对模型不同部位进行分段等厚分层；当模型存在尖端部位时，在该部位进行较小厚度分层，而在其他部位依然按照精度要求分层，这不仅保留了模型的局部特征，而且能够满足模型的某些部位的功能要求，更可观的是当模型超出快速成型设备的加工范围时，算法还可以按部位依次对模型进行实体加工[10]。

2.1 算法实现

STL模型是三维实体经过三角形网格化后得到以三角形面片3个顶点坐标和其法向量坐标为基础的文件格式。其表现形式如下：

本文算法对模型数据提取时，只提取表征该三角形面片位置信息的坐标数据，储存在一个区域内。各个三角形面片组成一个大的数据区域，即完成STL模型全部关键信息读取。程序利用MATLAB语言及其软件实现，基于等厚分层算法进行，将零件不同精度要求的各部位以及具有尖端的部位在分层方向上分段划分，使每一个部位对应在STL模型上的边界值按照从小到大的顺序输入程序，数据以行向量形式储存，这样就能将模型按照分层方向以数据形式存入到矩阵当中；若零件不同的部位要求不同的精度，将每一段部位对应的分层厚度依次输入程序，数据会储存在另一个行向量当中，这样保证了分层部位与其精度一一对应。这些是根据模型的精度要求进行输入，保证了分层的灵活性和可操作性。

模型分段完成后，基于等厚分层算法的优点，采用了基于STL模型三次排序的等厚分层策略。将STL模型每一个三角形面片的三个顶点按照其在分层方向的大小进行排序，然后按照顶点坐标在分层方向上的分量最大值的大小对所有三角形面片进行排序，将排序后的三角形面片按照分层方向从小到大依次进行求交，当给定某一分层平面时，将第二次排好序的三角形面片中顶点坐标分量最大值小于该分层平面的三角形面片删除，然后按照顶点坐标分量最小值再一次排序，将最小值大于分层切平面的三角形面片排除，提取出只与该分层切平面相交的三角形面片进行截交。这样不仅减少了算法所占用的内存空间，而且提高了分层效率。

本文的关键在于如何将不同精度要求的分段部位按照各自的精度要求进行等厚分层，上文已经将模型在分层方向上的各部位边界以行向量的形式输入，即将模型行划分为几段，每一段中的分层厚度不同。假设模型分为n个段，那么需要输入的精度也为n个，输入界限则是n+1个。模型分为n个部位，有n个精度要求，为了使每一部分按照各自精度进行等厚分层，将程序设为n个循环，按照模型在分层方向的大小，从小到大依次将模型各部分放入循环当中。将模型放入循环时，为了提高搜索效率和分层速度，用STL模型在分层方向所具有的特性，根据模型各部分边界值对三角形面片进行提取。当三角形面片顶点在分层方向上的分量最大值小于较小的分层边界时将其排除，当三角形面片的顶点在分层方向上的分量最小值大于较大的边界时也将其排除，提取剩余三角形面片，这些面片就是模型该部位包含的所有三角形面片。当其中的一部位开始进行分层时，先将这部位在分层方向上的边界高度值和分层厚度值以及提取出的三角形面片引入该次循环当中，将边界高度值按照其对应的分层厚度值组成等间距行向量，从该等间距行向量中提取出每一个元素，这些元素则是分层切平面的高度值，依据这一高度值对提取出的三角形面片按照上文提出的排序等厚分层算法进行分层，根据等间距行向量的长度值进行循环求交，直到该部位分层结束，自动转入下一部位进行下一次分层。分段分层中各段之间的衔接是该算法的一个关键环节，本算法巧妙地应用输入的边界值对模型各段进行限制，当模型分层超出该段分层部位时，为了不影响下一部位的分层，直接跳出循环，引入下一部位所需的所有元素。引入该部位所需元素后，则以该部位与上一部位共同拥有的边界值为起点开始进行分层，为了达到模型各部位之间的衔接，必须以该部位起点边界高度值对模型进行第一次截交，保证了模型在该部位的精度，使模型各部位之间顺利衔接，避免重复的求交过程。本文的求交运算是按照文献[11]的Trioutline函数，该求交算法无需建立模型的拓扑信息，直接对模型进行求交，无需建立其他连接关系，无需对交线段排序，直接获得封闭轮廓线。算法以分层制造的原理，边输出边制造，较大地节省了数据内存的占有量，减少了程序的运算时间。图1为算法的框架图。

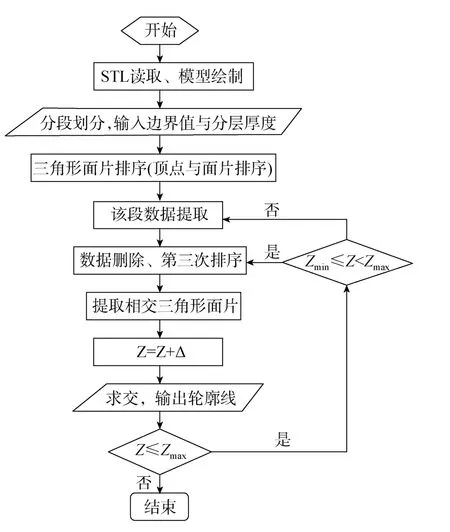
图1 算法的框架图

2.2 实例分析

快速成型技术要求分层算法具有较高的稳定性，并且在满足精度的前提下，能够很快地对模型进行分层运算，快速地输出快速成型机能够接受的分层轮廓线。在实际中，有些具有装配要求的较大尺寸零件(如文中斗齿，尤其是源于逆向设计的反求模型)，其某一部位(斗齿的封闭内腔和销孔具有装配要求)要求精度较高，而其他的部位又不需要较高的精度时：如果按照精度较低的要求，以较厚的层厚对模型整体进行制造，加工出的零件不能够满足其装配精度要求；而当以较薄的层厚对模型整体进行制造时，其加工时间又会大幅度增加，造成成型效率的降低，但若采用分段等厚分层算法，可以在精度和效率两个方面得到较好的协调。

下面通过图2所示斗齿点云对本文算法进行实例验证，并通过该斗齿的等厚分层实例与之相对比。整体分层和模型不同位置的分层效果。每一个例子都以ASCII的形式对STL模型进行读取。分层算法是在DELL N5010(处理器CPU：Intel(R) Core3)的Windows 7系统中安装的MATLAB R2010a编程语言环境下运行的。

该斗齿模型(由三维扫描点云转换得到其STL模型)尺寸：97.64 mm×222.00 mm×89.69 mm，面片个数：101462个，顶点个数：50727个。模型具有封闭内腔，且内腔又含有同心的两个销孔，内腔和销孔均为具有装配要求的重点部位，二者相较其他部位有明显的尺寸、形状和位置精度要求。综合考虑该模型的装配精度要求及使用时铲尖极易磨损破坏的情况，将其共分为5段，见图3～7。图8是整体分段分层结果，图9是较高精度的等厚分层结果。

图2 斗齿模型

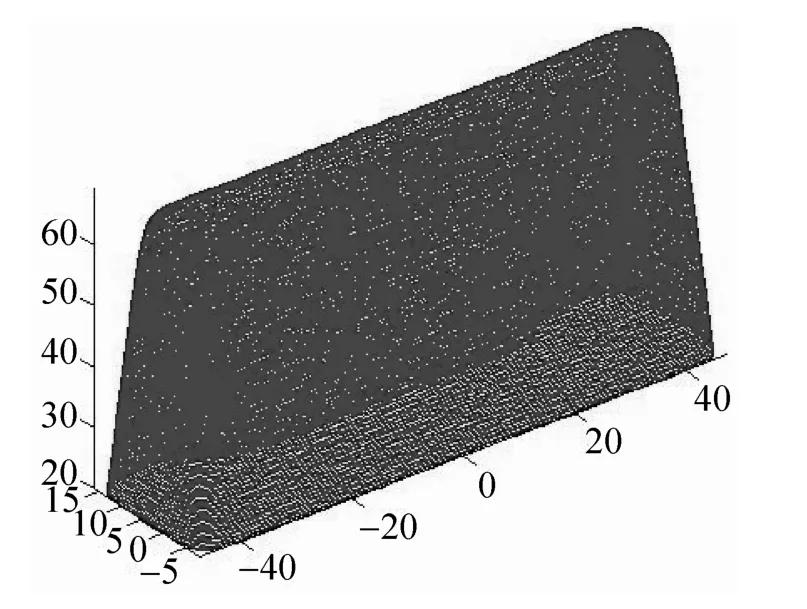
图3 顶端部位分层(层厚0.3，层数167)

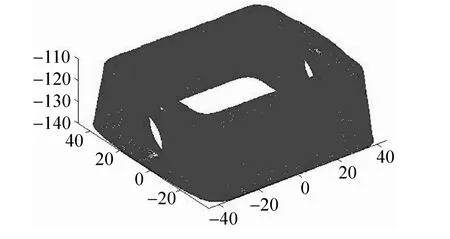
图4 销孔部位分层(层厚0.1，层数300)

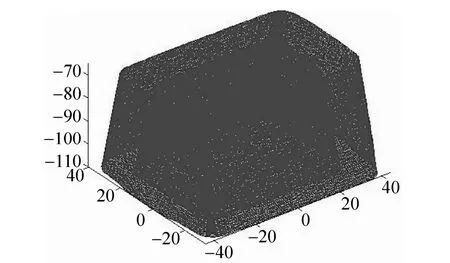
图5 孔上方内腔部位(层厚0.3，层数150)

图6 孔下方内腔部位(层厚0.3，层数41)

图7 其余部分层(层厚0.6，层数)

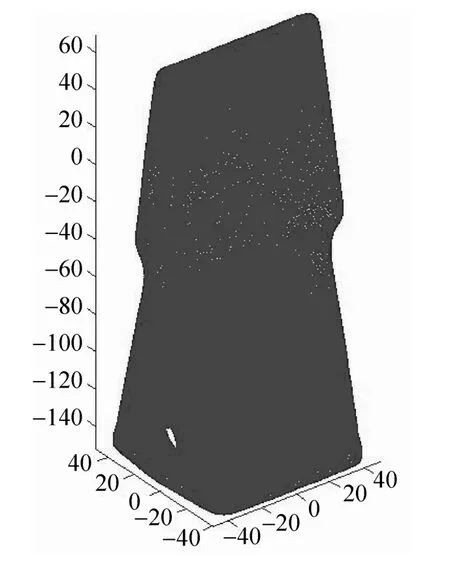
图8 整体分段分层图(层数799)

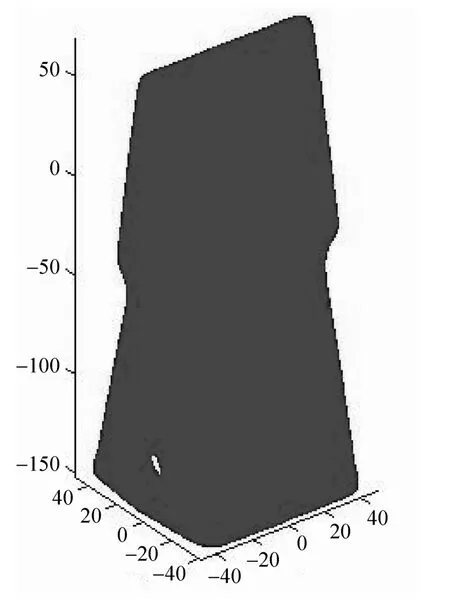
图9 整体分层图(层厚0.1，层数2220)

分段分层以不同层厚对模型进行分层，在满足精度情况的前提下，对各部位依次进行加工，同时从各段分层图显示，模型能够灵活地沿着分层方向对模型进行分层。通过分段分层图与等厚分层图对比，对于同一模型，两种分层程序在满足装配精度的前提下，分别以不同层数对模型进行分层，无疑显示出层数之间的差距。在同一设备条件、装配部位相同精度下，分段等厚分层算法分层效率是等厚分层算法的三倍以上。表1为斗齿分段分层与等厚分层时间对比。

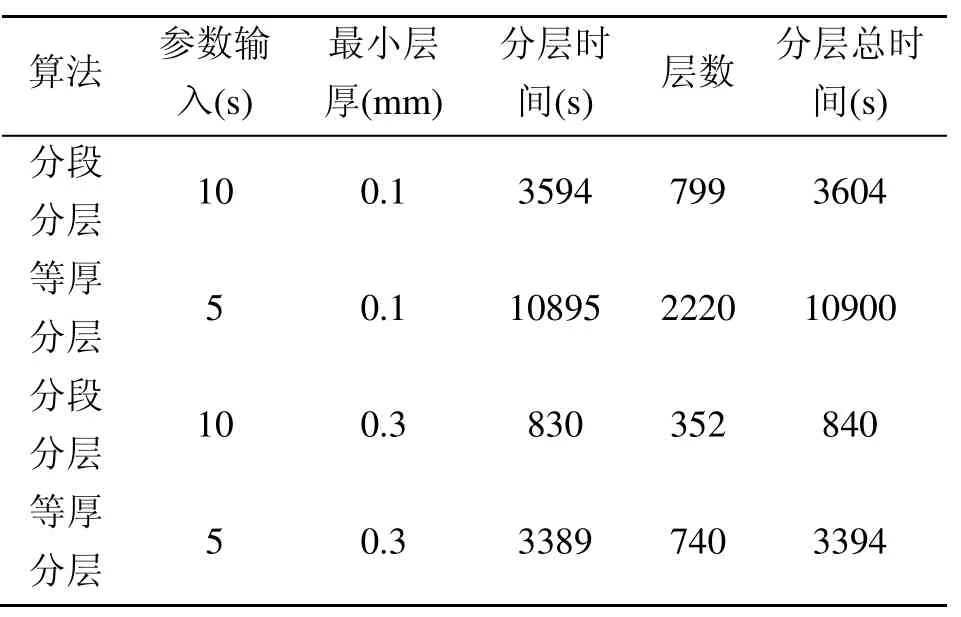
表1 斗齿在不同程序下的分层对比

3 结 论

对同一模型，在同一平台和计算环境下，分别采用分段分层和等厚分层策略，对装配和精度要求高的部位做同一精度的分层处理结果表明：

(1) 分段分层处理、及采用三次排序精简法不仅能够较为灵活地根据模型的装配和精度需要进行分层处理、避免重复的求交过程，而且使分层占用内存量二次减少、加快了分层处理过程，有利于提高成型效率。

(2) 分段分层处理所具有的灵活性，使本文算法能够对超出成型设备加工范围的模型进行分割，为分段加工大尺寸零件提供了分层软件方面的可能。

(3) 对于某些具有装配要求或需要区别分层精度的复杂成型零件，分段分层处理较等厚分层处理具有高效性，尤其适合用于此类零件的逆向设计。

以上仅为在MATLAB软件中进行的分层运算，如何将分段分层算法融合在现有快速成型设备中，以及发现并解决在融合过程中所暴露或产生的新问题，是笔者进一步研究的努力方向。

[1]Pan Haipeng, Zhou Tianrui.Generation and optimization of slice profile data in rapid prototyping and manufacturing [J].Journal of Materials Processing Technology, 2007, 187-188: 623-626.

[2]胡德洲, 李占利, 李涤尘, 丁玉成, 卢秉恒.基于STL模型几何特征分类快速分层处理算法研究[J].西安交通大学学报, 2000, 34(1): 37-40, 45.

[3]牟小云, 郑建明, 田静云.基于坐标分层的STL模型切片算法的研究[J].机床与液压, 2008, 36(7): 52-53, 72.

[4]李仲阳, 谢存禧, 杨家红.基于STL文件的快速成型分层算法与毗邻拓扑信息的快速提取[J].计算机工程与应用, 2002, 38(7): 32-35, 79.

[5]赵保军, 汪 苏, 陈五一.STL数据模型的快速切片算法[J].北京航空航天大学学报, 2004, 30(4): 329-333.

[6]胡德洲, 李涤尘, 洪 军, 赵万华, 丁玉成.快速成形制造中截面轮廓线快速生成算法研究[J].中国机械工程, 2001, 12(6): 54-56, 5.

[7]毕晓亮, 朱昌明, 侯丽雅.快速成型中的自适应切片方法研究[J].计算机应用研究, 2002, 19(4): 21-22.

[8]李仲阳, 谢存禧, 邵 明, 成晓阳.快速成型的精度分析与自适应分层的研究[J].广东工业大学学报, 2000,17(2): 15-19.

[9]张嘉易, 刘伟军, 王天然.三维模型的适应性切片方法研究[J].中国机械工程, 2003, 14(9): 750-752.

[10]赵吉宾, 刘伟军, 王越超.基于STL文件的实体分割算法研究[J].机械科学与技术2005, 24(2): 131-134.

[11]王春香，李振华.STL模型分层算法的优化及应用[J].机械设计与制造, 2013, (3): 87-90.