基于模糊逻辑的频谱分配算法
2014-03-20陈小丹凌洪涛
李 磊,李 莉,陈小丹,凌洪涛
(上海师范大学 信息与机电工程学院,上海 200234)
认知无线电(Cognitive Radio,CR)的提出,为实现频谱资源的高效利用提供了有效途径,它根据对可用频谱的分析结果,在不影响主用户正常使用的前提下,为有通信需求的认知用户分配适合的频谱[1].CR是以频谱检测为基础的,目前对于频谱检测的理论研究已经比较多[2-3],而在频谱检测的基础上,研究动态频谱分配是认知无线电的媒体接入层中的关键技术之一.
现有的经典频谱分配算法有基于图论、博弈论、频谱拍卖等算法.文献[4]是基于图论的,采用分布式频谱管理结构,每个节点在遵守频谱管理规则的条件下独立决策,保证了算法的公平性,降低了算法复杂度和时间开销,但是在某些应用环境可能导致将较多频谱资源分配给频谱需求量较小的节点,使得频谱的利用率较低.文献[5]基于博弈论提出了一个议价博弈的分布式分配算法,通过议价博弈,无需在每次拓扑结构变化时重新计算就能得到最优分配,同时兼顾了算法的公平性,但文中的议价博弈交易框架假设网络节点相互合作,而实际系统中的节点可能是自私的.文献[6]是基于频谱拍卖的,同时考虑复杂度和诚信,提出一种贪婪频谱分配算法,设计了基于临界邻居节点投标的定价机制来保证诚信拍卖,每次为最高出价投标者分配频谱,但在认知用户投标价格相同的情况下会导致频谱利用率的降低.文献[7]考虑了认知用户的频谱利用率、认知用户移动性、信噪比等因素,利用模糊逻辑系统得到认知用户的频谱接入概率,但是未考虑到认知用户与认知用户基站的距离等因素的影响,并且频谱接入概率的计算公式较复杂.
基于以上算法的优点与不足,本文作者提出一种利用模糊逻辑的频谱分配新算法.本算法是在可用空闲频谱数量少于认知用户数量的前提下,采用集中式的频谱分配方式,认知用户将频谱检测信息通过上行控制信道传送给认知用户基站,在认知用户基站中执行所提出的频谱分配算法,目标是使基站收益最大化.
1 算法设计
1.1 系统模型
图1是认知无线电的集中式网络拓扑图,假设一个主用户的授权频带处于空闲状态,多个认知用户相互竞争该空闲频带,主用户、每个认知用户都拥有独立的接收机和发射机,主用户与主用户基站通信,认知用户与认知用户基站通信.认知用户基站通过测量获得或接收认知用户发送的相关数据,执行频谱分配算法后把该空闲频带分配给其中一个认知用户.
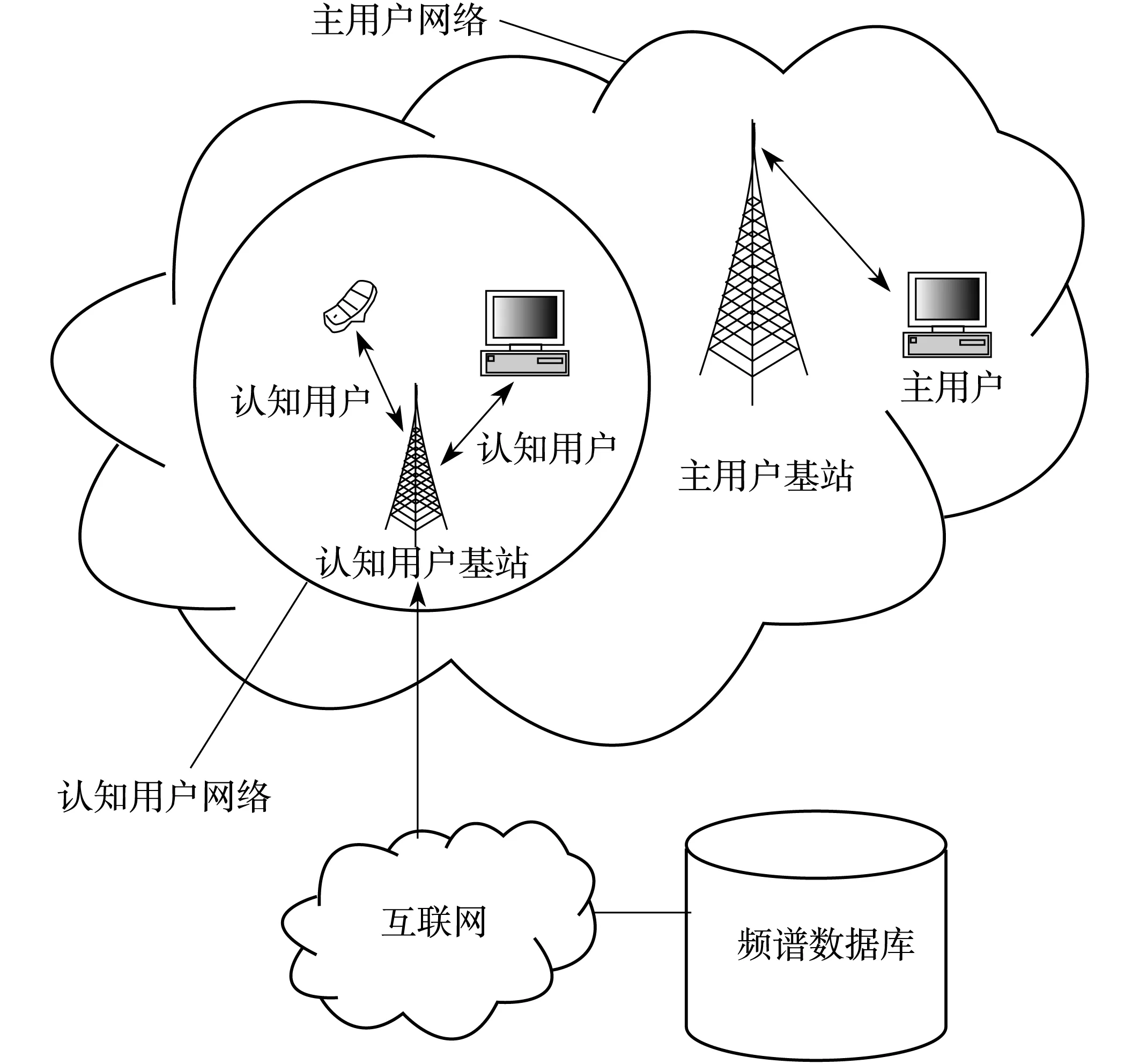
图1 集中式网络拓扑图
设认知用户基站有一个大小确定的信号覆盖面积,基站收发台不能覆盖的区域就是信号的盲区.基站发射和接收信号的范围直接关系到认知用户终端信号在这个区域内的好坏.通常认知用户与认知用户基站的距离越近,信道条件就越好,有利于认知用户的通信.不失一般地,设需要使用某一空闲频谱的认知用户与认知用户基站的距离为RBS,定义该认知用户的通信优先级Q为RBS的倒数,如式:
Q=1/RBS.
(1)
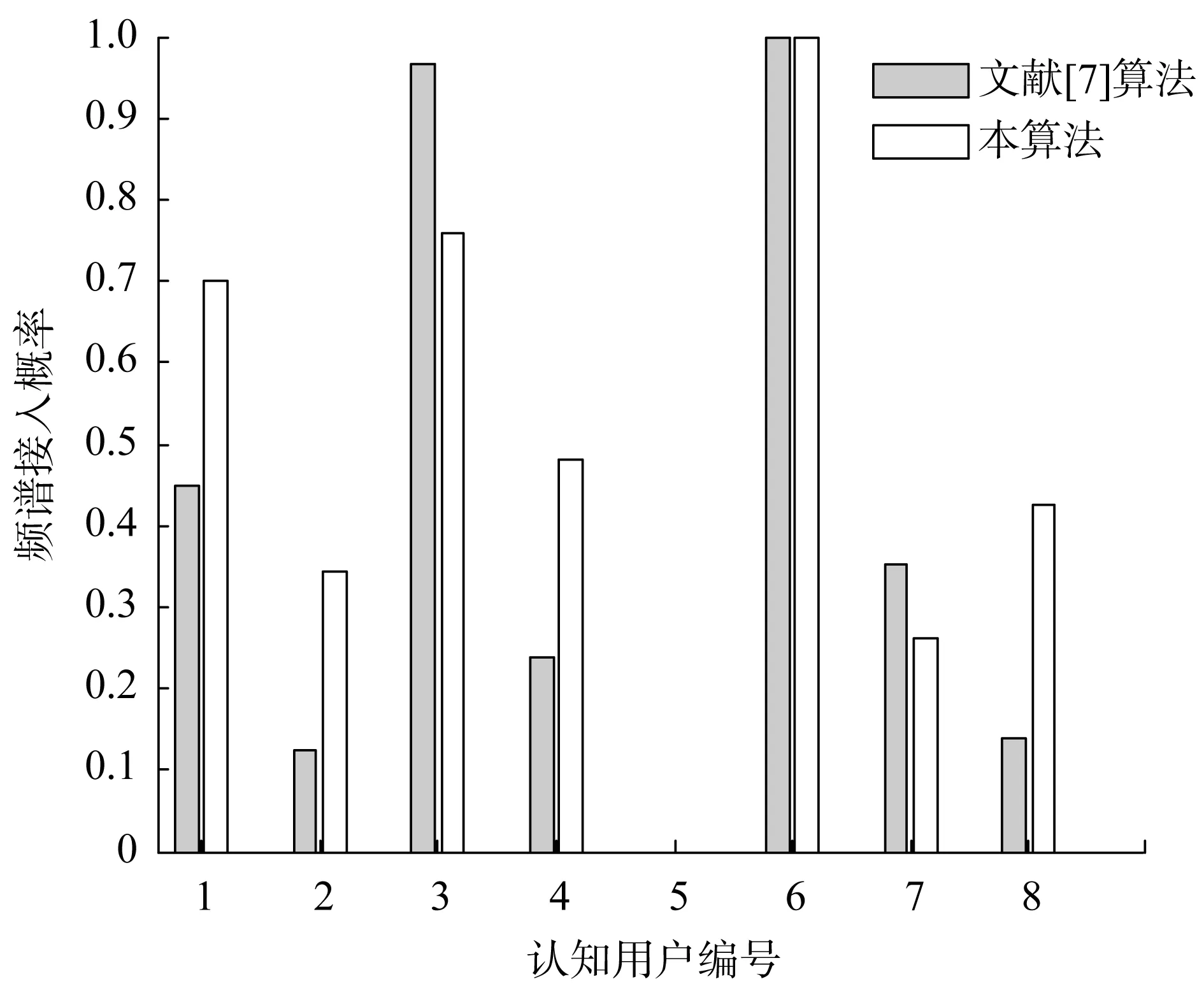
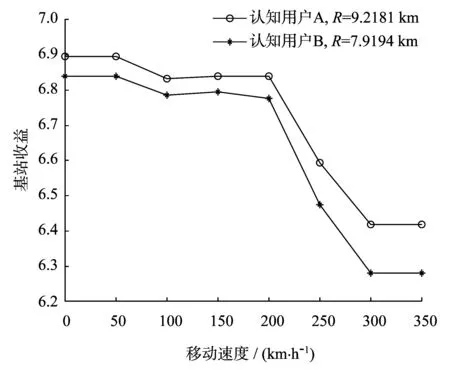
当RBS增大到认知用户基站的小区半径Rth时,认知用户信道条件可认为差,甚至可能处于信号盲区,故把Rth值代入式(1),对应的Q值定义为通信优先级门限Qth.那么,对于一个需要接入该空闲频带的认知用户,若其Q 影响模糊逻辑系统设计的因素很多,其一,主用户暂时不使用的频带是固定的,而每个认知用户所要进行的业务却不确定,例如可能是数据、多媒体业务和单纯的话音业务,那么不同认知用户的频谱利用率就不同,具有较高频谱利用率的认知用户对频带的利用更充分;其二,当认知用户处于运动的状态下,认知用户的接收机和发射机能够处于稳定的收发状态至关重要,这时就要考虑多普勒频移的影响,通常情况是移动速度越快,信道条件越差,不利于通信;其三,认知用户使用空闲频带的前提条件是不影响主用户的正常通信,一般是认知用户发射机距离主用户接收机越远越好,这样对主用户通信造成的干扰小.此外,还有空闲频带的可用性等,由于图1所示的系统模型已明确当主用户不使用空闲授权频带时认知用户才能接入,所以这里不再考虑该因素. 基于以上分析,选择认知用户的频谱利用率、移动速度、认知用户发射机与主用户接收机之间的距离作为三输入模糊逻辑系统的输入条件,经过模糊化、设置控制规则、解模糊化的过程,得到认知用户的频谱接入概率,如图2所示为三输入模糊逻辑系统框图. 图2所示的模糊逻辑系统的3个输入参数的模糊化特性如下: 图2 三输入模糊逻辑系统框图 定义频谱利用率ηS[7],如式: (2) 式(2)中,BWs是认知用户需要使用的频带,BWa是总的可用频带. 表1 模糊规则表[7] 为保证频带分配的有效性,ηs的取值范围设为[0,1],当ηs∈[0,0.5)表示频谱利用率低,ηs∈(0.2,0.8)表示频谱利用率中等,ηs∈(0.5,1]表示频谱利用率高.根据以上规定把频谱利用率的高低程度分为3种标记,如式: Fηs={低, 中等, 高} . (3) 每一种标记唯一对应一个隶属概率函数,ηs的隶属概率函数如图3(a)所示. 3G LTE对终端移动速度的要求是,0~15 km/h最优,15~120 km/h处于高性能,120~350 km/h可以正常通信,350~500 km/h仅部分频带可用[8].设认知用户移动速度VSU的最大值是350 km/h,对该最大值做归一化处理后,VSU∈[0,0.5)表示认知用户移动性低,VSU∈(0.2,0.8)表示移动性中等,VSU∈(0.5,1]表示移动性高.根据以上规定把认知用户移动性的高低程度分为3种标记,如式: FVSU={低, 中等, 高} . (4) 表示VSU的隶属概率函数如图3(a)所示. 认知用户发射机与主用户接收机之间的距离为R,R越大则认知用户对主用户正常通信的干扰就越小.设R最大取值10 km,对该最大值做归一化处理后,R∈[0,0.5)表示认知用户与主用户距离近,R∈(0.2,0.8)表示距离中等,R∈(0.5,1]表示距离远.根据以上规定把认知用户与主用户距离的远近程度分为3种标记,如式: FR={近, 中等, 远} . (5) 表示R的隶属概率函数如图3(a)所示. 图3 隶属概率函数 最后,考虑模糊规则的结论模糊集,设P是每个结论模糊集中认知用户接入频谱的概率,其大小程度分为5种标记,如式: FP={非常低, 低, 中等, 高, 非常高} . (6) P取值范围设置为[0,1],取值范围为[0,0.3)表示接入概率非常低,取值范围为(0.1,0.5)表示接入概率低,依此类推,P的隶属概率函数如图3(b)所示. 在模糊逻辑系统的3个输入值ηs、VSU、R属于3种模糊程度的隶属概率函数已知条件下,模糊逻辑系统可判定输入值ηs、VSU、R所属的模糊程度;查询如表1所示的模糊规则表,确定对应的模糊规则序号,按相应序号的规则并利用最大-最小方法进行模糊推理,得到认知用户的频谱接入概率的模糊程度集合. 利用重心法将频谱接入概率的模糊程度集合解模糊化,得该认知用户的频谱接入概率P,如式: (7) 通信优先级高且频谱接入概率大的认知用户,则认为其接入该空闲频带后通信效果更好.因此,定义认知用户的通信优先级与其频谱接入概率之积为认知用户基站收益,如式: M=P·Q. (8) 最后,认知用户基站将该频带分配给使基站收益最大的认知用户.认知用户基站会检查是否还有其他能被分配的空闲频带,若有,则针对该频带执行一次算法进行分配;若没有,则整个频谱分配过程结束. 基于模糊逻辑的频谱分配流程图,如图4所示. 图4 基于模糊逻辑的频谱分配流程图 设有n个认知用户竞争1个空闲频带,那么计算这n个认知用户带来的基站收益,需要考虑式(1)、(2)、(7)和(8).由式(1)、(2)和(8)可知分别要进行n次乘法运算,对于式(7),每使用一条模糊规则视为一次加法运算[9],那么计算n个认知用户的频谱接入概率最多需要进行8n次加法运算、16n次乘法和16n次积分运算,积分运算可认为是对梯形面积的计算.则本算法的计算复杂度为: (9) 同样推理,可得文献[7]在同样前提下执行一次算法的最大计算复杂度为: (10) 在使用相同数量的模糊规则时,本算法的复杂度要低于文献[7]的算法. 参考相关资料可知,3G LTE支持的基站小区最大覆盖半径为100 km,当小区覆盖半径在5 km以内时系 表2 仿真参数设置表 统的吞吐量最大[8].仿真中假设认知用户基站小区覆盖半径为1 km,将该距离代入式(1)可得到Qth=1.仿真中系统的其他参数设置如表2所示. 在不同的认知用户频谱利用率、认知用户移动速度、认知用户发射机与主用户接收机之间的距离的输入值条件下,模糊逻辑系统得到不同的频谱接入概率.不失一般地,图5给出的频谱接入概率是将相应算法计算所得的频谱接入概率对其最大值做了归一化处理的结果. 图5的仿真结果表明:本算法对比于文献[7]的算法,在输入值相当的情况下,两种算法得到的认知用户频谱接入概率是接近的,但本算法复杂度更低. 图5 频谱接入概率 图6 认知用户移动速度对认知用户基站收益的影响认知用户A、B:ηs=0.606 8,RBS=0.109 1 km 图6所示为认知用户移动速度对认知用户基站收益的影响的曲线图.图6中两个认知用户A、B的频谱利用率ηs和认知用户与认知用户基站的距离RBS相同,但认知用户发射机与主用户接收机之间的距离R是不同的.由图6可知,同一认知用户带来的基站收益是随着其移动速度VSU的增大而减小的,这是因为移动速度越大,模糊逻辑系统计算得到的频谱接入概率越小.不同认知用户在相同移动速度下带来的基站收益是不同的,认知用户A带来的基站收益更大,这是因为认知用户A的发射机与主用户接收机之间的距离更远,模糊逻辑系统计算得到的频谱接入概率更大. 本文作者在可用空闲频带数量少于认知用户数量的前提下,采用集中式的频谱分配方式,将认知用户基站的信号覆盖面积问题转化成对每个认知用户的通信优先级进行划分,而对认知用户的频谱利用率、移动速度、认知用户发射机与主用户接收机的距离等物理因素,则设计三输入的模糊逻辑系统进行模糊逻辑运算,得到了每个认知用户的频谱接入概率.认知用户的通信优先级与其频谱接入概率之积定义为基站收益,频谱分配的目标是基站收益最大化. 本文作者提出的算法在频谱分配的过程中能使基站收益最大化.仿真证实了该方法的可行性.与文献[7]得到的频谱接入概率是接近的,但计算复杂度较文献[7]降低.然而,执行一次算法不能分配多个频带,下一步要关注的是怎样解决该问题.如何在可用空闲频带数量不少于认知用户数量的认知无线电网络下进行频谱分配,也需要进一步地研究. 参考文献: [1] AKYILDIZ I F,LEE W Y,CHOWDHURY K R.CRAHNs:Cognitive radio ad hoc networks[J].Ad Hoc Networks,2009,7(5):810-836. [2] YUCEK T,ARSLAN H.A survey of spectrum sensing algorithms for cognitive radio applications[J].IEEE Communications Surveys & Tutorials,2009,11(1):116-130. [3] HUANG L,LI L,ZHANG J,YE P.Wideband Spectrum Sensing Based on Multi-Resolution Bayes Classifier for Cognitive Radio[C].In Proc IEEE ICC,Ottawa:IEEE,2012. [4] CAO L,ZHENG H.Distributed rule-regulated spectrum sharing[J].IEEE Journal on Selected Areas in Communications,2008,26(1):130-145. [5] CAO L,ZHENG H.Distributed spectrum allocation via local bargaining[C].Sensor and Ad Hoc Communications and Networks,Santa Clara:IEEE,2005. [6] ZHOU X,GANDHI S,SURI S,et al.eBay in the sky:Strategy-proof wireless spectrum auctions[C].Conference on Mobile Computing and Networking,San Francisco:ACM,2008. [7] HONGSAM T Le,HUNG DLy.Opportunistic Spectrum Access Using Fuzzy Logic for Cognitive Radio Networks[C].Proceedings of 2008 IEEE Second International Conference on Communications and Electronics,Hoi An Vietnam:IEEE,2008. [8] INLKYOUNG C,ILKYOO L,YOUN O P.Study on Coexistence between Long Term Evolution and Digital Broadcasting services[J].International Journal of Advanced Science and Technology,2012,38(1):75-92. [9] ZHANG W Z,LIU X C.Centralized Dynamic Spectrum Allocation in Cognitive Radio Networks Based on Fuzzy Logic and Q-Learning[J].China Communications,2011,8(7):46-54.1.2 模糊逻辑系统设计



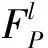
1.3 算法描述
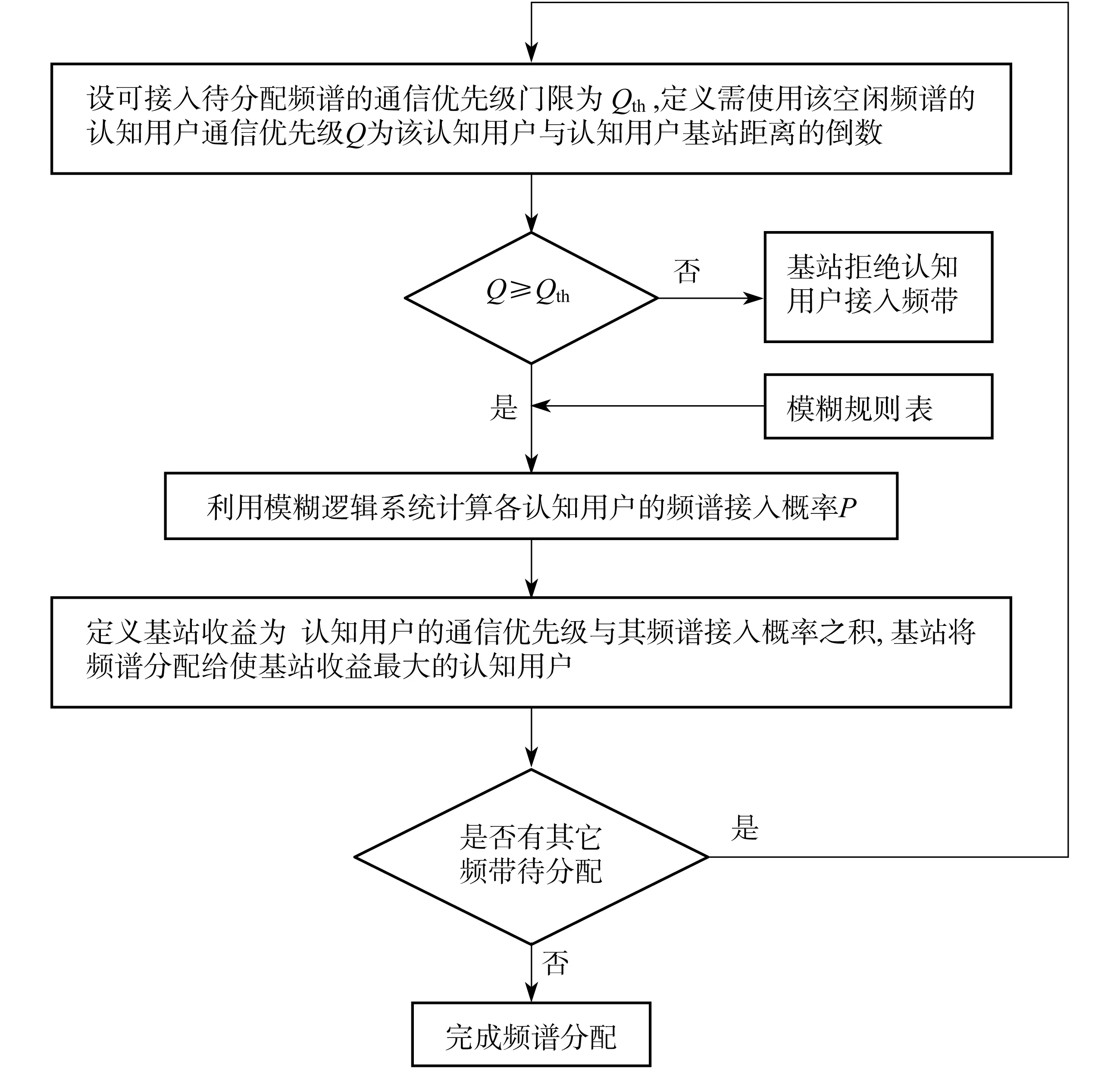
1.4 算法复杂度
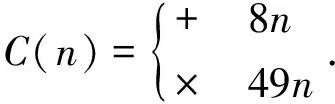
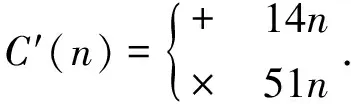
2 仿真与分析

3 结束语
