协作室内定位优化算法

石 莹, 赵梗明

(上海师范大学 信息与机电工程学院, 上海 200234)

无线网络技术的发展和覆盖率的增加,使得人们在随时随地使用无线网络资源时,对自身位置信息的需求量不断提高.尤其在室内环境下,能够快速准确地获得移动终端的位置信息变得日益迫切.与此同时,协作移动定位已经开始逐渐步入新型无线定位方式的行列,随着无线通信技术的发展和处理数据能力的不断增强,对于精确位置信息方面的科学技术领域也成为十分具有潜力的实验课题和研究方向.

针对于无线室内定位误差过大的问题,本文作者利用协作的思想,进行优化算法设计.通过仿真实验验证,所设计的优化算法相对于传统的三角质心定位,可以减小它的定位误差,从而达到提高位置估算精确度的目的.

1 传统三角质心定位法

三角质心法是在定位算法中利用率较高的一类定位算法.由于在实际情况中环境内的各种干扰,使得到达待测节点的RSSI值小于理论上的RSSI值,这也就使得理论模型中的3个圆的半径过大,从而出现3个圆的交集域[1-3],如图1所示.

在这个交集域中,分别设3个顶点为E、F、G,则三角质心算法的思想是,以△EFG的质心定义为待测节点的位置.由此建立方程组,如式(1),分别联立方程组1和方程组2,可以求得以A为圆心和以B为圆心的2个圆的2个交点坐标,这时需要判断哪个交点距离点C更近,则定义为G点(选择保留),另外一个舍弃.同理,计算出E、F点的坐标值.

(1)

另外一点值得注意的是,当以A、B、C三点为圆心,以三点到待测节点的距离为半径的3个圆(如图2)没有交点时,则表示这组数据无法通过三角质心算法计算待测节点坐标,应给予舍弃处理[4-5].

图1 三角质心法

图2 3个圆不相交的情况

2 协作通信

在协作无线通信中,主要考虑节点之间通过协作的方式增加定位精度.在一个协作通信系统中,需要每一个节点都可以传输数据并可以作为其他节点的协作代理.

协作通信可以使代码率增加而传输功率降低.对于传输功率的降低,有两方面原因.一方面是因为协作通信不仅仅是2个节点时间的传递信息,而是所有节点同时传输数据;另一方面是因为分集的有利因素,使得所有节点的底层传输功率降低.若假设系统中所有的参数恒定不变,那么降低传输功率是有利的.

同样,从系统运行速率上看,协作通信会使系统率降低,而信道代码率升高.这是由于在一个协作通信系统中,每一个节点为其他节点发射自身相关信息,这样就会到导致系统率降低.同时,协作分集的有利影响使得每个节点的频谱效率增加,这也导致了信道代码的提高[6].

待测节点-已知节点链路和待测节点-待测节点链路中的RSS数据都可以运用在协作定位过程当中.假设待测节点M的坐标为{X(i)=[x(i),y(i)]T,i=1,…,nm},而已知节点S的坐标为{X(j)=[x(j),y(j)]T,j=1,…,ns}.Soork等人提出的最小二乘目标函数[7],如式(2)所示:

(2)

式(2)中,p(i)[j],α(i)[j],d(i)[j]是Mi～Sj之间的接收功率,α参数和距离;p(i)(m),α(i)(m),d(i)(m)是Mi～Mm之间的接收功率,α参数和距离.通过公式(2)计算出J(X)的最适应点,并给出了所有待测节点的位置估计.

3 基于协作的室内定位优化算法设计

本设计的主要思想为:利用协作定位的方法,不仅对已知节点与待测节点之间传递信号进行测量,而且对待测节点之间传递的无线信号也进行测量,从而获得更好的定位精度及鲁棒性.当所有关于已知节点和待测节点的自身信息与相对信息均传递到PC机后,PC机立刻估算出待测节点的“绝对”位置.

根据传统三角质心算法获得M1,M2坐标分别为(X1,Y1),(X2,Y2),计算M1,M2间的距离d1.通过M1,M2之间的RSSI值,根据自由空间路径损耗模型计算得出距离d.

RSSI=Pr(d0)-10n×lg(d/d0)+Xσ,

(3)

(4)

则可求得Δd:

Δd=|d-d1| .

(5)

此时,设计两种基于协作思想的,针对于未知节点为两种的定位优化算法.此两种优化算法均是在d(利用通过传统质心定位算法求得的两点距离)的基础上,根据d1(两点之间RSSI值求得的两点距离)进行坐标优化定位.

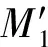
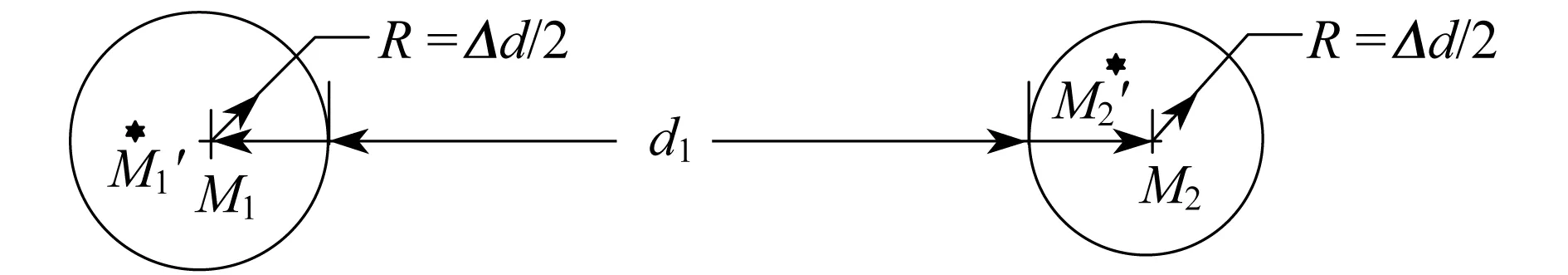
图3 圆域型优化算法的图示(两个待测点)

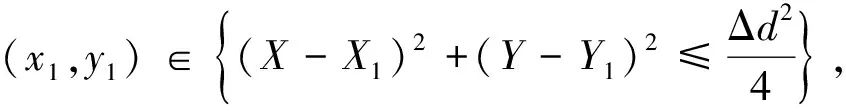
(6)

(7)

M={(x1,y1),(x2,y2)|min|(x1-x2)2+(y1-y2)2-d|},

(8)

(9)

4 仿真实验

4.1 图象分析

为了简单直观地看出定位优化的结果,现将通过传统三角质心法、直线型优化算法、圆域型优化算法3种方法分别定位5次的仿真误差进行比较,如图4所示.

图4 定位误差比较

从图4中可以看出:

(1) 经过与圆域型优化算法相结合后,在大部分情况下,优化后的定位均可达到定位误差减小的目的;

(2) 在优化结果上看,与圆域型优化算法相结合后,定位误差被优化程度不定.

4.2 数据分析

分别列举出利用传统三角质心法和三角质心算法与圆域型优化算法相结合的优化定位算法定位20次的误差进行比较,如表1所示.

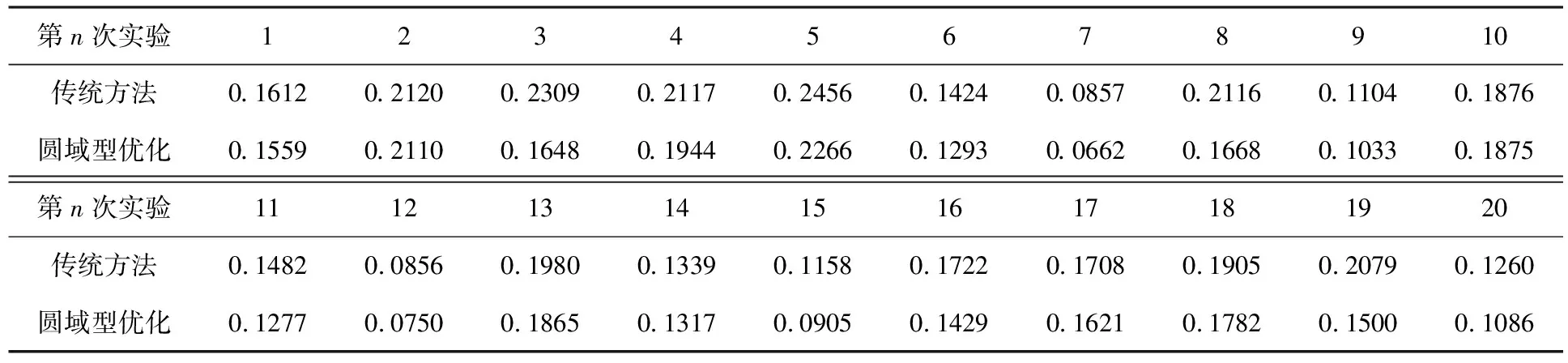
表1 误差对比

从误差数据中,可以计算出以下对比数据(以下数据均由此20组数据得出),如表2所示.分析可得：

表2 误差分析数据对比

(1) 圆域型定位优化算法在实际定位优化中,确实可以减少定位误差.可以得出:经过圆域型优化算法优化后的三角质心定位算法相对于传统三角质心算法的定位精度约提高11.62%.

(2) 经过优化后的定位算法在优化最大值与优化最小值方面的误差数据,经计算,获得一些数据结论.

在优化误差最大值方面:圆域型优化算法相对于传统三角质心算法,误差约减小7.74%.

在优化误差最小值方面:圆域型优化算法相对于传统三角质心算法,误差约减小22.66%.

从此数据中看出经过优化后的定位算法相对于传统定位算法在定位误差范围上也有一定的优化效果,特别在误差最小值方面效果更为突出,优化误差程度可在原来误差基础的1/5以上.

(3) 为了进一步说明优化后的定位算法在定位优化上的作用,分别列出这20组实验数据与传统三角质心定位算法相比较的优化程度(即提高精确度),如图5所示.

图5 优化程度折线图(20次实验)

其中优化程度最大的一组为第3组,优化程度为28.63%.优化程度最小的一组为第10组,优化程度为0.05%.在这20组实验中,与圆域型优化算法相结合后定位算法在定位方面表现出良好的优化定位效果,而且值得注意的是这种优化算法使得每次的定位误差都会产生不同程度上的优化效果.

5 结束语

本文作者对原有的三角质心室内定位算法进行改进,利用协作定位的思想,通过未知节点与未知节点的通信再次对定位的坐标进行优化.考虑到定位误差的优化方式问题,将优化方式与定位信息相结合进行优化.通过仿真实验证明,定位优化算法可以在平均误差方面、误差范围方面、优化程度方面都有显著的效果.在未来的优化算法研究中,可以考虑将遗传算法应用到圆域定位优化算法中,使定位达到更加精确的效果.

参考文献:

[1] 林玮,陈传峰.基于RSSI的无线传感器网络三角形质心定位算法[J].现代电子技术,2009(2):180-182.

[2] 朱剑.基于RSSI均值的等边三角形定位算法[J].东北大学学报:自然科学版,2007,28(8):1094-1097.

[3] 张兴会,张志辉,邓志东.基于RSSI测距技术的三角形面积和定位算法[J].电子测量技术,2008,31(11):92-98.

[4] 邓宏彬.一种基于无线传感器网络的星球漫游机器人定位算法[J].机器人,2007,29(4):384-388.

[5] 张兴会,邓志东.基于无线传感器网络的地下矿工定位算法[J].计算机测量与控制,2008,16(12):2003-2005

[6] NOSRATINIA A,HUNTER T E, HEDAYAT A.Cooperative communication in wireless networks[J].IEEE Communications Magazine,2004,42(10):74-80.

[7] SOORK A S,SAADAT R, TADAION A A.Cooperative mobile positioning based on received signal strength[C]∥International Symposium on Telecommunications 2008(IST 2008).Tehran:IEEE,2008.