地热井井筒热效应研究

刘志涛，张志胜，胡松涛，吕明荟，谭现锋

(1.山东省鲁北地质工程勘察院，山东 德州 253015；2.山东省地矿工程勘察院，山东 济南 250014)

地热井水位变化特征与普通水井有所不同，在进行地热研究中，有时候会发现一些奇怪的现象，比如有的地热井在开采时的动水位埋深会小于之前的静水位。这貌似很不科学，实际上是由于未考虑水的密度随温度变化的影响，将不同水温条件下的水位直接相比，从而得出的错误结果。目前习惯上称上述现象为井筒效应，实际上油田上油气研究中也有该词，但所研究问题完全不同。鉴于问题的关键在于温度，因此认为称之为井筒热效应或温度效应更合适。该文对井筒热效应的机理进行了简要分析，对目前普遍采用的水位校正方法进行了论述，提出了进行水位校正的新的计算方法，并通过具体实例将新方法与传统方法进行了对比分析。

1 简要机理分析

水位实际是含水层压力的反映，含水层压力使其能够支撑起一定高度的水柱，在某一时刻，井筒内水柱压力与其密度、水柱高度存在如下关系：

p=ρgh

(1)

式中：p—井内水柱压力(Pa)；ρ—水的密度(kg/m3)；g—重力加速度(m/s2)；h—井内水柱高度(m)。

水的密度不是恒定的，随温度变化而变化，也就是说，不同的水温对应不同的密度，由式1可知，当井内水柱压力水一定时，不同的水密度会对应不同的水柱高度，即水位是不同的。因此最终结果是，不同的温度对应不同的水位。

在普通水井中，由于井内水柱高度不大，井内温差小，水的密度差别也较小，因此由井筒热效应引起的水位偏差很小，基本可以忽略。而对于类似于鲁北地区这种深埋型地热水，其地热井深度均达上千米，最深2000余米[1-2]，不同情况下井内水温有着较大差别，因此必须考虑井筒热效应对其水位进行校正，否则不仅可能会严重影响到所计算水文地质参数的精确度[3]，甚至会给研究带来错误的结论。

2 水位校正方法

根据上述井筒热效应机理可知，如果能测得井内水柱压力，便可通过式1计算出拟定温度下的水柱高度，进而换算出水位标高或埋深。而实际上，由于受观测条件的限制，在进行地热水位动态监测或抽水试验时，很少能直接测得水柱压力，一般观测的数值都是当时条件下的水位埋深，这时需要先计算出井内水柱压力，进而进行水位校正。由于此时井内水柱温度和密度一般不是恒定的，因此利用观测数值并不能很精确地计算出水柱压力。目前一般的做法是通过一些假定条件，将问题简化，从而进行近似计算。根据各方面研究资料，目前有2种简化方法，根据其计算原理，可以分别称之为“平均密度法”和“平均温度法”。另外，该文也提出了一种新的计算方法，即“积分法”。

2.1 平均密度法

该方法计算井筒内水柱压力的公式[4]为：

(2)

式中：ρK，ρB分别为井口水温(或液面水温)和井底水温对应的水密度(kg/m3)；其他符号同前。

该计算公式虽然未明确说明，但隐含着一个假定条件，即井筒内水柱平均密度为井口水温与井底水温对应水密度的平均值，更进一步说，该公式假定井筒内水柱密度与深度呈线性关系。这里就存在一个问题，因为实际上它们很可能并不呈线性关系，因此井口与井底水密度的平均值并不等于平均密度。但在开采条件下，式2还是适用的，因为此时井口水温与井底水温差值一般很小，密度相差也很小，水密度与深度可近似视为线性关系。而在静水条件下，液面与井底水温一般相差很大，如鲁北地区一般都在30℃以上，这种情况下，用式2校正水位偏差就稍大了，并且当液面与井底水温相差越大，其偏差就越大。当然也可定性预测，如图1所示，假定液面和井底密度分别为a，b点对应密度，按平均密度法，井筒内水柱平均密度为线段ab中点即c点的密度(c点纵坐标)，而实际上井筒内水柱密度随温度按弧段ab变化，实际平均密度必定大于c点密度，因此式2所计算的水柱压力偏小，进而得出的水位埋深偏大。

图1 水密度与温度关系曲线图(根据《地热资源地质勘查规范》附录C表C.2)

2.2 平均温度法

这是天津地热勘查开发设计院经常采用的方法，它假定井筒内水柱温度与深度呈线性关系，这时井口温度与热储温度(即井底温度)的平均值即为井内水柱平均温度，然后根据该平均温度下的水密度计算水柱压力，进而换算为水位，其计算公式为[注]天津地热勘查开发设计院，宗振海、王继革、高亮等，山东省临沂市罗庄区东部LR-1单井地热资源勘查报告，2012年。：

(3)

式中：h—校正后水位埋深(m)；H—取水段中点的埋深(m)；h1—观测水位埋深(m)；ρ平—井筒内水柱平均密度(kg/m3)(即井口温度或液面温度与热储温度的平均值所对应的水密度，静水条件下为液面温度与热储温度的平均值所对应的水密度)；ρ高—热储温度对应的水密度(kg/m3)；其他符号同前。

该公式是按热储温度进行水位校正，若要校正为其他温度下的水位，将式3中热储密度ρ高改为其他温度对应的密度即可。这种方法也存在一个问题，尽管假定了井筒内水柱温度与深度呈线性关系，但由于水密度与温度并不呈线性关系(图1)，因此平均温度所对应的水密度实际上并不等于井筒内水柱的平均密度。同样，由于开采条件下井口水温与热储温度差值一般很小，水温与密度可近似视为线性关系(如图1中db段)，因此该方法在动水条件下还是较为精确的。而在静水条件下，假定井筒内密度变化在弧段ab之间，按式3其平均密度为e点密度，并不一定等于实际平均密度，因此也存在一定偏差。

2.3 积分法

根据鲁北地区众多地热井测温资料，其温度随深度增加而较为均匀地升高，没有很大的突变，因此如平均温度法，这里也假定井筒内水柱温度与深度呈线性关系。另外，在一些油气资源井筒传热模型研究中[5]，也经常有相同的假定。根据水密度与温度试验值[6]，通过曲线拟合，发现在5～100℃(一般地热井内水温变化都在该区间内)，密度与温度符合如下关系式(图1)。

ρt=-0.0034t2-0.092t+1001.1

(4)

式中：ρt-t温度(℃)下的水密度(kg/m3)。

根据假定条件，任意深度h处水温t可用式5表示。

(5)

式中：t1,t2,t分别为h1，H和h深度对应的水温(℃)；k=(t2-t1)/(H-h1)，井筒内水柱增温率(℃/m)；其他符号同前。

由式1、式4、式5，用积分可求得井筒内水柱压力为：

(6)

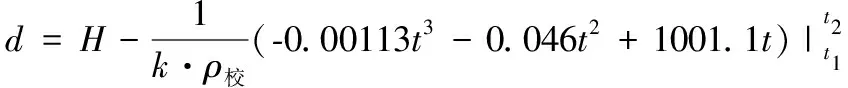
(7)

式中：ρ校为拟校正温度对应的水密度(kg/m3)；其他符号同前。

另外还有一个特殊的情况，当井口、井底温度相同，即t1=t2时，k=0，式7无法计算，此时井筒内水柱温度和密度恒定，可根据式1直接进行计算，最终得出的水位埋深校正公式与式3相同。这种特殊情形主要发生在大流量抽水的情况，实际上在进行地热研究中，很少直接去测量热储温度，而是将大流量抽水时的水温作为热储温度。

该方法弥补了平均温度法的不足，从理论上讲更精确些，当然其计算要比平均温度法稍微麻烦，但在计算机技术广泛应用的今天，尤其是在进行批量计算时，也并不比平均温度法繁琐。

3 计算实例

以鲁北地区某地热井为例，对其观测数据分别按以上3种方法进行水位校正，并进行对比分析，以说明井筒热效应的影响以及3种方法计算结果的差别。该地热井热储平均埋深1393.5m，热储温度54℃，主要用于供暖，其观测水位埋深和液面温度如图2所示。

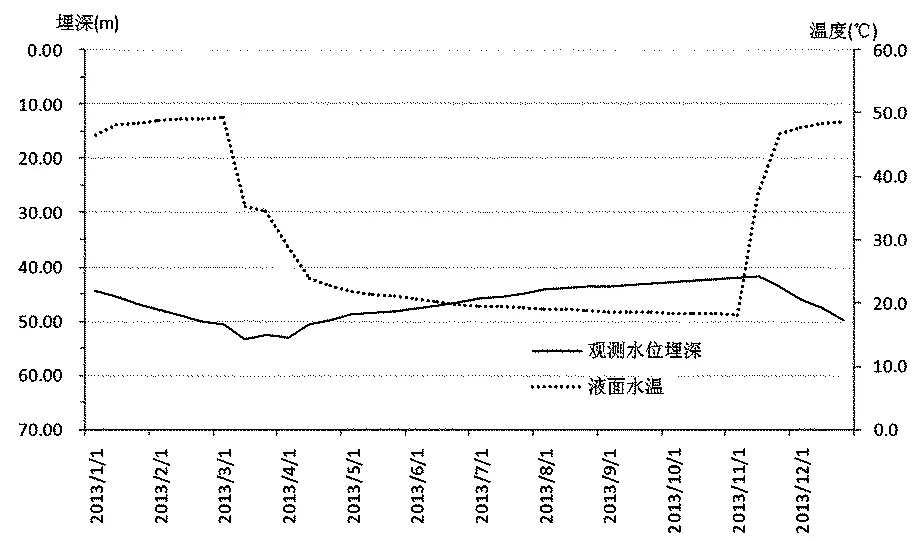
图2 观测水位埋深和液面温度动态曲线图

3.1 积分法校正结果分析

用积分法计算出井筒内水柱压力(g取9.81)，并分别校正为常温20℃和热储温度54℃下的水位埋深(图3)。根据计算结果，54℃下校正水位埋深均小于观测水位埋深，差值在1.47～9.30m；20℃下校正水位埋深均大于观测水位埋深，差值在7.20～14.83m。以上2种情形有一个共同特点是，动水条件下(开采期)差值较小，静水条件下较大。而54℃和20℃下校正水位埋深差值在16.29～16.49m，动水和静水条件下差值变化不大。另外，在3月底至4月初，即停暖后初期，观测水位埋深有一个先减小后增加然后又减小的过程，但水柱压力却一直呈现增加趋势，校正后水位埋深也一直呈现减小趋势，而后者明显符合实际规律。以上都说明了地热研究中必须要考虑井筒热效应，否则可能会出现很大的偏差。

图3 井筒水柱压力及校正后水位埋深动态曲线图

3.2 校正结果对比分析

分别按前述3种计算方法将观测水位埋深校正为20℃下的水位埋深，校正后水位埋深动态曲线如图4所示。根据计算结果，平均密度法校正后埋深要大于积分法，差值在0.03～1.00m，动水条件下相差很小，基本可忽略，静水条件下相差较大，这也说明了平均密度法更适用于动水条件的情况。平均温度法校正后埋深小于积分法，但两者计算结果更接近些，即差值要小些，在0.01～0.49m，也是动水条件下的差值小。以上是校正为20℃下埋深的情形，若要校正为更高一些温度下的埋深，各方法计算结果相比差值会有所增加，如该例中，当校正为热储温度54℃的埋深时，各方法校正结果的差值与20℃时的差值相比，最高仅增加0.01m，几乎可忽略，也就是说，当校正温度升高或降低时，以各方法校正的水位埋深基本以相同幅度减小或增加。

图4 不同方法校正水位埋深动态曲线图(20℃)

4 结语

进行地热研究必需考虑井筒热效应，否则会严重影响研究成果，甚至可能得到错误结论。根据各种水位校正方法计算原理，平均温度法和积分法假定条件更符合实际情况，因此计算结果精度要优于平均密度法，积分法与平均温度法假定条件相同，但弥补了平均温度法中的不足，因此计算结果精度优于平均密度法。但不管多么精确，与实际情况肯定还有差别，由于没有井底压力的实测数据，其偏差具体有多大，目前尚不能确定，留待今后进一步深入研究。

参考文献：

[1] 赵季初.鲁北砂岩热储地热尾水回灌试验研究[J].山东国土资源，2013,29(9)：24-27.

[2] 杨询昌，王成明，冯守涛，等.德州市城区地热水动态与开采量关系[J].山东国土资源，2011,27(7)：27-29.

[3] 陈国富，陈虹雁，王学工，等.井筒内水头高度与井底压力对比试验[J].工程勘察，1997，25(4)：32-35.

[4] 周训，陈明佑，赵维明.深层地下热水钻井井内动水位升高值的计算[J].勘查科学技术，2000，18(5)：33-34.

[5] 刘杰，段永刚，何玮.高温井井筒温度分布计算方法[J].重庆科技学院院报，2010，12(1)：190-192.

[6] GB/T11615-1010，地热资源地质勘查规范[S].