GPS高程拟合方法探讨

2014-03-20夏永成樊宽林

水电站设计 2014年1期

关键词：重力场合法曲面

夏永成,樊宽林,刘非

(四川中水成勘院测绘工程有限责任公司，四川成都 610072)

1 前言

利用GPS测量得到的高程是基于WGS-84椭球的大地高。由于我国的高程是正常高系统，是建立在似大地水准面基础上的，它们之间的关系是：

Hr=H84-ζ

(1)

ζ是该点的高程异常(见图1)。知道了各点的高程异常就可以求出各点的正常高。

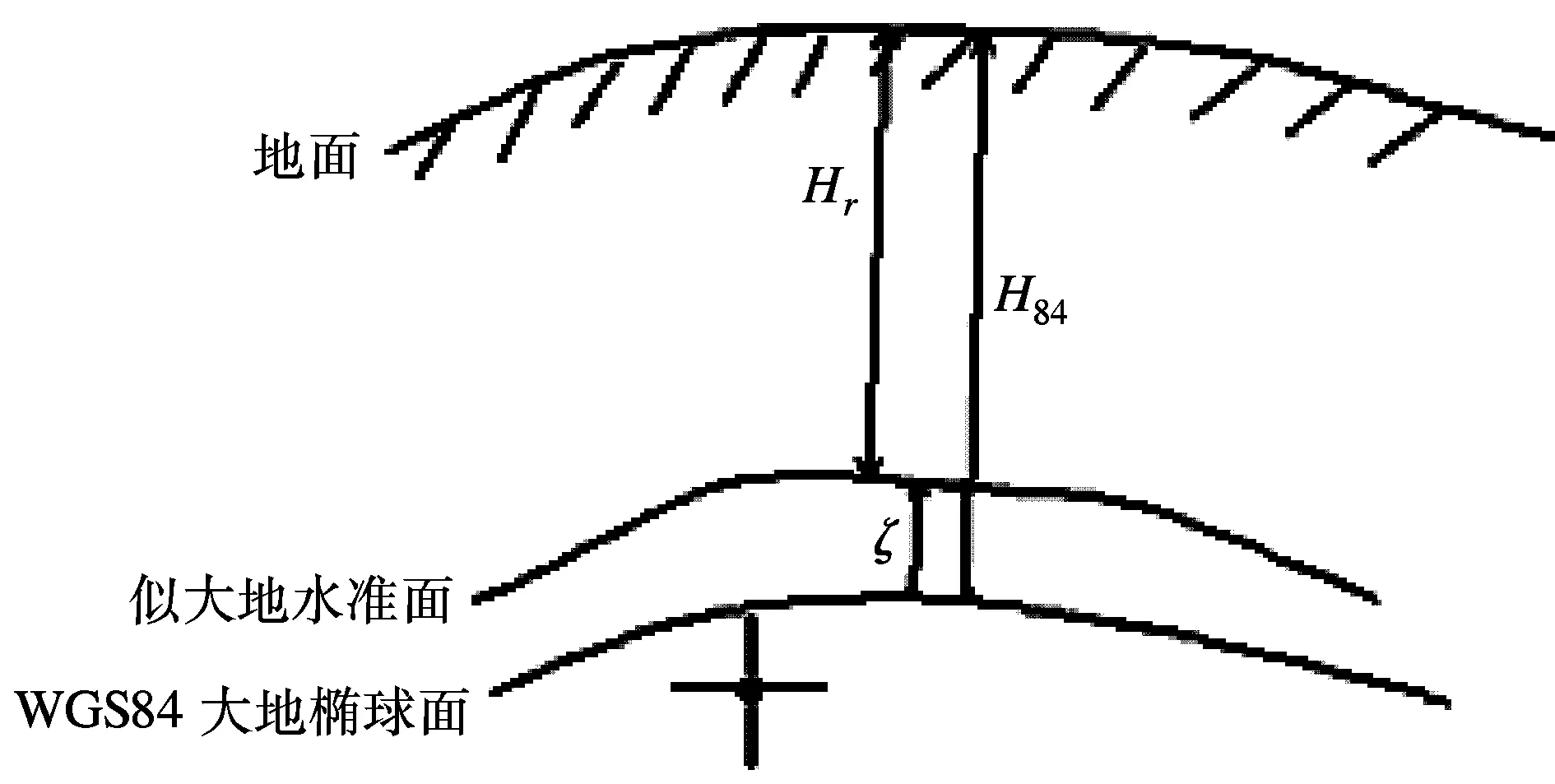
图1 高程异常示意

目前求解高程异常的方法很多，主要是数值逼近法，分为函数模型逼近和统计模型逼近。函数模型逼近的最大优点是对趋势性变化效果拟合效果较好；统计模型的特点是计算灵活，对稳态随机过程的逼近效果较好。常用的函数模型逼近法有解析内插法(包括曲线内插法、样条函数法和Akima法)、曲面拟合法(包括平面拟合法、多项式曲面拟合法、多面函数拟合法、曲面样几条拟合法和移动曲面拟合法)等。还有一些其他方法如：地球重力场法和地形改正法，神经网络模型法和基于灰色系统理论的灰关联法等。

2 几种常用的拟合方法及特点

2.1 多项式拟合法

设点的ζ与点的位置信息(x,y)有以下关系

ζ=f(x,y)+ε

(2)

式中f(x,y)为ζ中趋势值；ε为误差。

设f(x,y)=a0+a1x+a2y+a3x2+a4y2+a5xy+…

(3)

写成矩阵形式有：

ζ=XB+ε

(4)

对于每个已知点，都可以列出以上方程，在ΣεTPε=min的条件下，可以解出

B=(XTPX)-1XTPζ

(5)

再代入式(3)求高程异常，最后按式(1)求出Hr。

2.2 多面函数法

设点的ζ与点的位置信息(x,y)有如下关系

(6)

式中ai为待定系数，Q(x,y,xi,yi)为核函数，xi、yi为已知点坐标。核函数一般选用具有对称性的距离型即：

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+σ]1/2，

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+σ]-1/2

(7)

上两式分别称为正双曲面函数和倒双曲面函数。σ为光滑系数为一常数，可由试验给定。

当待求点数等于已知点数时，任一点ζP为

ζP=QPQ-1ζ=(Q1PQ2P…

(8)

式中，Qij=Q(x,y,xi,yi)。当待求点多于已知点数时，

ζP=QP(QTQ)-1ζ

(9)

2.3 移动曲面法

一般对某一内插点，(xj′,yj′),若数据点(xi,yi)满足

(xi-xj′)2+(yi-yj′)2≤R2

(10)

可用这些数据点参加内插，则称以(xj′,yj′)为圆心，半径为R的圆形移动窗口内曲面内插。

设移动到第j个内插点(xj′,yj′)时，利用落入该点移动窗口内的m个数据点(xi,yi)上的观测值ζi(i=1,2,…m),以下列多项式

ζi=a0+a1x+a2y+a3xy

(11)

计算第j个内插点函数值。在m个数据点上建立如下误差方程：

令

Vi=a0+a1xi+a2yi+a3xiyi+ζi,Pi

(12)

Pj=diag(P1,P2,…Pm)Xj=(a0,a1,a2,a3)T,

w(d)为权函数，目前广泛使用的权函数有

w(d)=exp(-d2/a2)

(13)

w(d)=1/(1+d2/a2)

(14)

a为常数，可由试验给定，一般取数据点平均距离的两倍。应用最小二乘原理解得

(15)

代入(11)可得该点的高程异常。

移动曲面计算法在计算时，通常采用契比雪夫多项式为移动多项式。

2.4 地球重力场模型法

地球重力场模型是依据重力场理论导出的计算重力异常等的数学模型，它是利用最新的卫星跟踪数据、地面重力数据、卫星测高等重力场信息计算得到的重力位的球谐函数级数展开的系数[4]。根据给定的重力场模型的位系数Cnm、Snm可用下式计算各点的高程异常：

sinmL)Pnm(sinB)

(16)

式中ρ、B、L——分别为计算点的矢径、纬度和经度;

GM——为引力常数与地球质量的乘积；

γ——为计算的正常重力值；

a——为参考椭球的长半轴；

Cnm、Snm——为完全规格化位系数；

Pnm(sinB)——为完全规格化缔合Legendre函数；

N——为地球重力场模型展开的最大阶数；

m——为次。

若给定一组位系数就确定了一个相应的地球重力场模型，就可以求出该点相对于此模型的高程异常。

目前国际上公开的比较有代表性的EGM96模型,它是美国NASA/GS-FC和国防制图局联合研制的360阶全球重力场模型，相当于全球55Km分辨率。它在美国本土分辨率为50Km，精度达到几厘米，在我国精度只有米级，因此难以直接应用于生产，但它包含比较准确的重力场长波信息[3]，可用于更高精度的GPS高程拟合。

2.5 各种拟合方法的特点

多项式拟合法是在拟合区域的已知高程点之间按削高补低的原则构造一个多项式曲面(线)拟合区域的似大地水准面。当拟合范围大，高程异常变化大，拟合的误差就越大。拟合多项式的阶次越高，拟合面产生震荡的可能性增大。模型的自适应程度较低。

多面函数是一种纯数学的逼近方法，它是在待求点上与每个已知点上建立函数关系，这种函数关系表现为一规则的数学曲面，将这些曲面按一定比例迭加起来就可以拟合出任何不规则的曲面。它的核函数是距离的函数，顾及了待求点与已知点之间的相关性，起着权系数矩阵的作用。

移动曲面法用有限区域内所有已知点来拟合该点的高程异常，该区域随着拟合点的位置变化而移动，可以更好地模拟该区域的似大地水准面。该法精度较高，自适应程度较好[5]。

地球重力场模型法的精度随着地点的变动而变化，当该区域的所测重力数据没有参与建模或参与建模的数据少时，计算出的重力异常精度就低，该区域参与建模的重力数据多时精度就高。但利用它计算出的高程异常能准确反应该区域高程异常的变化趋势。鉴于它们的这些特点，综合起来衍生出另一种方法——基于地球重力场模型的拟合法。

3 基于地球重力场模型的拟合法

基于地球重力场模型的拟合法把高程异常分为长波信息和短波信息，用地球重力场模型计算长波信息，用逼近函数计算短波信息。它的原理是拟合出用地球重力场模型计算的高程异常误差的函数，然后用函数计算出的高程异常误差，再加上该点在地球重力场模型中计算的高程异常。设根据地球重力场模型计算出该点的高程异常为ζGM，该点的高程异常误差为ε，则有

H84+ζ=H84+ζGM+ε

(17)

移项得

ε=ζ-ζGM

(18)

ζ为该点的实际高程异常。令ε=f(x,y)，f(x,y)为文中所述的拟合函数，利用最小二乘法推估求得内插点的高程异常误差ε，再代入上式可求得该点的高程异常，最后用高程异常加上该点的大地高得到该点的正常高。这种方法通常被叫做“移去-计算-恢复法”。

4 几个问题

4.1 参数的选取

在拟合过程中参数的选取是很关键的，常见的是以该点的坐标为参数，这样拟合时所组成的法方程的系数很大，求解待定系数ai的误差会增大。当用坐标为参数时可以先对它进行中心化，这样可以减少其计算精度的损失。中心化的模型如下：

(19)

Xi′=Xi-ΔX,Yi′=Yi-ΔY

(20)

4.2 权的选取

4.3 精度评定

高程拟合的精度评定是通过内符合精度和外符合精度体现的。

内符合精度μ

(21)

式中n为参与拟合计算的已知点的残差V的个数。

外符合精度M

(22)

式中V为检核点的高程异常与拟合高程异常之差，n为检核点的个数。

外符合精度能客观地反映拟合的效果。当所选的已知数据点刚好位于所选模型附近时，内符合精度很高，它并不代表未知点有同样的拟合精度。因此进行精度评定时要把内外符合精度权衡比较。

5 数据实验

某高山峡谷区水电规划测绘布设的GPS控制网见图2，一共30个GPS点。平均边长4.1km，测区平均海拔2 650m。平面等级为D级，高程按四等三角高程联测。

图2 GPS网形示意

下面我们用以下四种方案进行高程拟合，设观测值都为等权观测。

方案一：用其中的6个点，以点的北京坐标为参数用二次六项式直接拟合高程异常；

方案二：先用EGM96拟合高程异常中的长波部分，求差后再用其中的6个点用一次三项式拟合高程异常之差；

方案三：同方案二，只是将已知点的个数增加为9个；

方案四：先用EGM96拟合高程异常中的长波部分，求差后再用其中的9个点用二次六项式拟合高程异常之差。四种拟合方法的精度结果见表1：

表1 四种拟合方法精度比较 m

从表1可以看出：基于地球重力场模型的GPS高程拟合法采用合适的数学模型精度高于单纯的多项式拟合法，该方法随着已知点的增多精度会提高，但当已知点增加到一定数量后精度不会进一步提高，这是由于多项式的runge现象造成的；方案二、三外符合精度相当，但方案二已知点个数只占所有点数的20%，因此方案二比方案三更为实用(见表2)。