某水电站边坡失稳涌浪计算分析
2014-03-20陈匀序
赵 明,陈匀序,朱 艳
(中国水电顾问集团成都勘测设计研究院,四川 成都 610072)
1 前 言
某水电站边坡在高程2 155m平台以上从2010年4月开始出现变形,2011年3月蓄水变形速率加快,且监测成果显示,深度35~40m范围内出现较为明显的变形;高程2 155m平台以下边坡从2011年3月蓄水开始出现变形,但内观监测资料显示,内部变形不大、尚未形成滑面,变形主要是浅表风化卸荷岩体的局部变形、破坏;变形体整体边坡在蓄水后表现为表部强风化、卸荷岩体的局部破坏,整体的滑动趋势不明显。
根据稳定计算分析,高程2 155m平台以上开挖边坡在各种工况下的抗滑稳定安全系数均满足规范要求,失稳的可能性不大;高程2 155m平台以下边坡存在局部失稳的可能,但其规模较小、且大部分在正常蓄水位以下,即使失稳滑动也不会产生危及大坝的涌浪;整体边坡稳定性较差,在各种工况下的抗滑稳定安全系数均不能满足规范要求,存在局部甚至整体失稳下滑的可能。
根据边坡地质稳定性评价、变形监测资料及边坡稳定计算成果综合判断,边坡可能存在以下三种失稳模式:
第一种失稳模式: 高程2 155m以下边坡浅表层在库水位作用下首先失稳、继而逐渐向内侧剥落式塌滑直到高程2 155m平台以下全部失稳,最后高程2 155m以上边坡失稳下滑。
第二种失稳模式:高程2 155m平台首先全部失稳,继而高程2 155m以上边坡失稳下滑。
第三种失稳模式:高程2 155m平台以上、以下边坡整体一次性失稳下滑。
从边坡现状稳定分析结果可知,高程2 155m以下边坡浅层、整体边坡存在局部或整体失稳可能性。需要分析边坡失稳产生的涌浪对大坝的影响。
2 计算方法
2.1 滑坡速度
潘家铮法采用条分法来计算滑坡的速度,计算采用改进的条分方法,选取了沿滑面方向和垂直滑面方向来建立平衡方程,然后用基本运动学原理求解块体的运动速度。
假定条块发生位移时按刚体运动,根据牛顿第二定律:
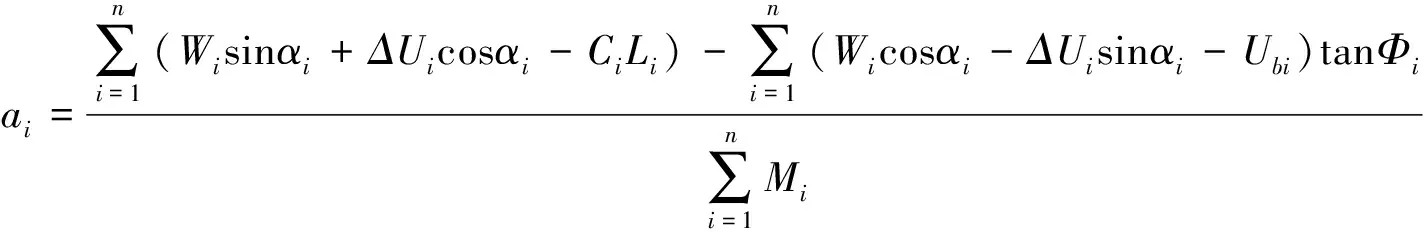
对于每一条块,设初速为Vi1,末速为Vi2,滑动距离为Li,滑动时间为Ti,进一步可得:
这样就可求出条块滑入水库时的速度及滑块运动的时间。
2.2 涌浪高度
计算采用潘家铮法对涌浪进行预测分析。潘家铮法是利用库水“单向流”分析成果,并采取一些假定来分析较为复杂的水库涌浪问题:
(1) 涌浪首先在滑坡入水处产生,产生初始波,然后向周围传播,在传播过程中不断变形,但忽略能量损耗或假定损耗为已知。
(2) 忽略边界条件的非线性影响,假定全部涌浪过程可以视为一系列源点处产生的小波影响的线性叠加。
(3) 每个小波成分都是孤立波,以涌浪形式在水面上传播,波速为常数。
(4) 假定涌浪达到对岸后发生全反射,或其反射系数为已知值。
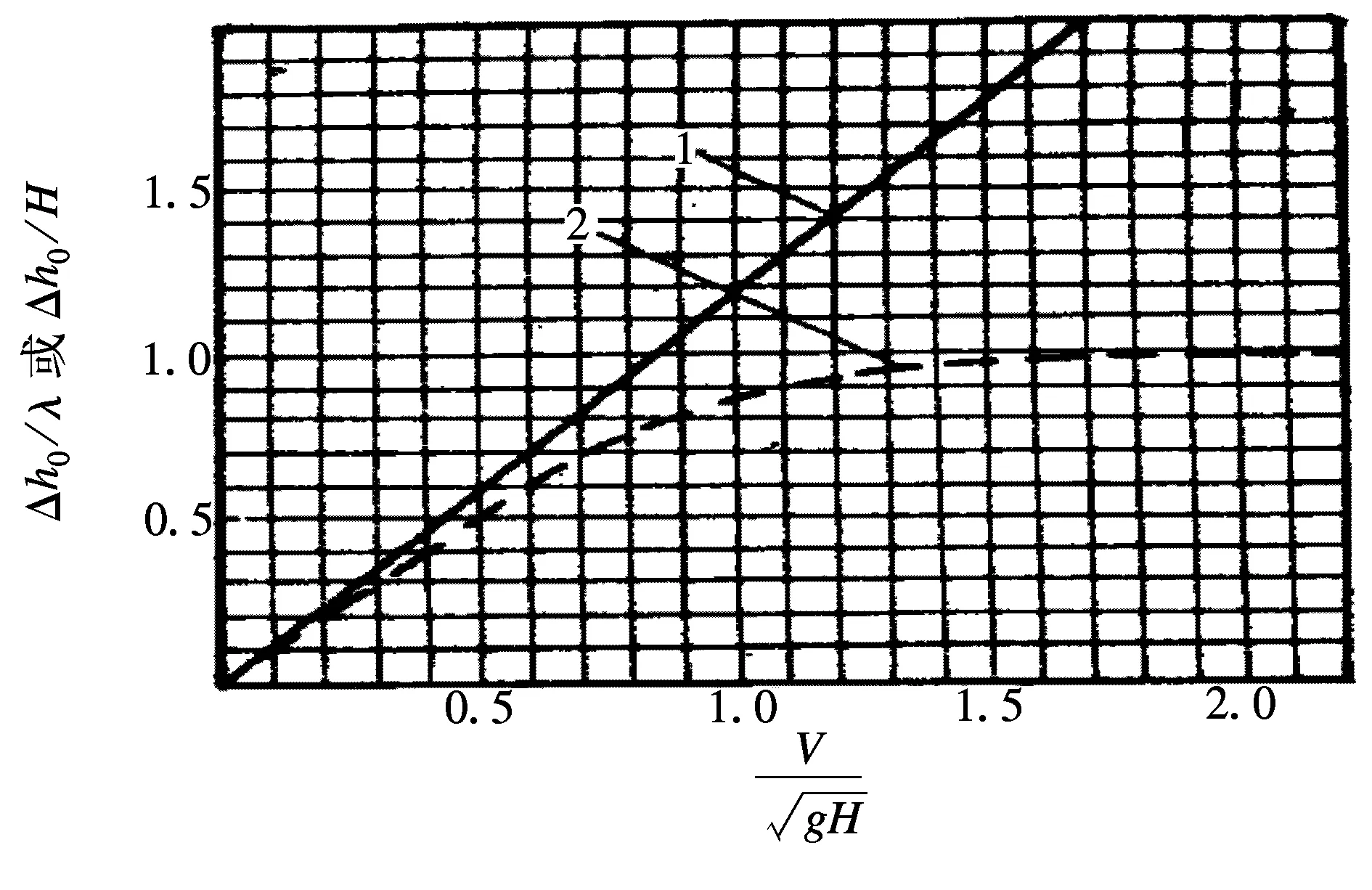
(5) 假定水库库岸为两条平行陡壁,宽度为B,滑坡范围L内的库岸断面一致,岸坡变形率为常数,且发生在时段0 2.2.1 滑坡涌浪初始最大浪高 当岸坡发生水平运动时,激起的初始浪高可表示为: 式中ξ0——激起的初始涌浪高度,m; h——水库平均深度,m; v——为岸坡水平运动速度,m/s; g——重力加速度,m/s2。 当岸坡发生垂直运动时,激起的初始浪高可用下面的函数表示为: 两种模式下的变化曲线见图1: 2.2.2 对岸及下游坝址点涌浪高度 潘家铮法计算滑坡对岸涌浪浪高公式如下: 图1 两种模式下的初始涌浪高度求解曲线注:1-岸坡水平运动模式;2-岸坡垂直运动模式 潘家铮法计算下游坝址点涌浪浪高公式如下: 式中ξ——对岸涌浪高度; ξx——对岸下游坝址处产生的涌浪高度; ξ0——初始浪高; k——波的反射系数,一般值为0.85~0.95,求对岸浪高时,可取为1.0; ∑——级数之和,其项数取决于滑坡历时T及涌浪从本岸传播到对岸的时间△t=B/c;波速c按下式计算: θn——传播到计算点的第n次入射角与岸坡法线的交角,按下式计算: x——计算点至滑坡中心点的距离; x0——计算点至滑坡上游边界的距离; L——滑坡体沿库岸的宽度,其半长用l表示; 计算边界条件根据地质资料确定、在不同水库水位下,边坡失稳时的滑动速度计算成果见表1~3。 边坡在不同水库水位、不同滑动模式下在坝址处产生的涌浪高度(边坡分阶段失稳下滑存在时间差,因此不考虑不同阶段失稳下滑所引起的涌浪叠加)计算成果见表4~6。 表1 滑坡速度计算成果(第一种失稳模式) 表2 滑坡速度计算成果(第二种失稳模式) 表3 滑坡速度计算成果(第三种失稳模式) 表4 边坡失稳产生的涌浪高度计算成果(第一种失稳模式) 表5 边坡失稳产生的涌浪高度计算成果(第二种失稳模式) 表6 边坡失稳产生的涌浪高度计算成果(第三种失稳模式) 从表4~6中可以看出,无论是在死水位2 063m还是正常蓄水位2 133m,当边坡以第一种、第二种破坏模式失稳下滑、或者在死水位运行期间边坡以第三种破坏整体下滑时,其产生的涌浪均不会超过坝顶高程;但当水库水位在正常蓄水位2 133m时,如边坡以第三种破坏模式失稳且滑速大于5m/s时,其产生的涌浪将极有可能漫坝。为保证大坝运行安全,需要对边坡进行治理,防止边坡整体下滑或延缓其下滑速率。 潘家铮法将滑坡体垂直分条块后,假设各条块为刚体,其运动轨迹能较好地模拟实际滑面情况,但是以下几个问题值得探讨: (1)运动过程是连续的,没有考虑滑坡体各块体在运动过程中相互碰撞及滑体与外部物体相互碰撞所引起的能量损失,因而其计算结果偏于保守。 (2)在滑动过程中,未考虑水的阻力,实际滑动过程中滑速越大,水体对滑坡体的阻力也越大,因而其计算结果偏于安全。 (3)滑面摩擦系数对滑速影响很大,而动摩擦系数目前尚难以准确确定,仅凭借工程经验取值,在以后的工程实践中值得进一步探讨。 [1] 潘家铮.建筑物的抗滑稳定和滑坡分析[M].北京:水利出版社,1980:92-95. [2] 哈秋黔,胡维德.水库滑坡涌浪计算[J].人民黄河,1980(2):407-411. [3] 汪洋.水库库岸滑坡速度及其涌浪灾害研究[R].武汉:中国地质大学(武汉).2005:51-55.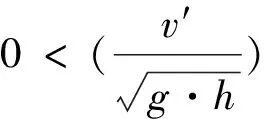

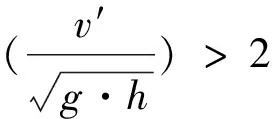
3 计算成果
3.1 滑坡速度计算
3.2 涌浪高度计算



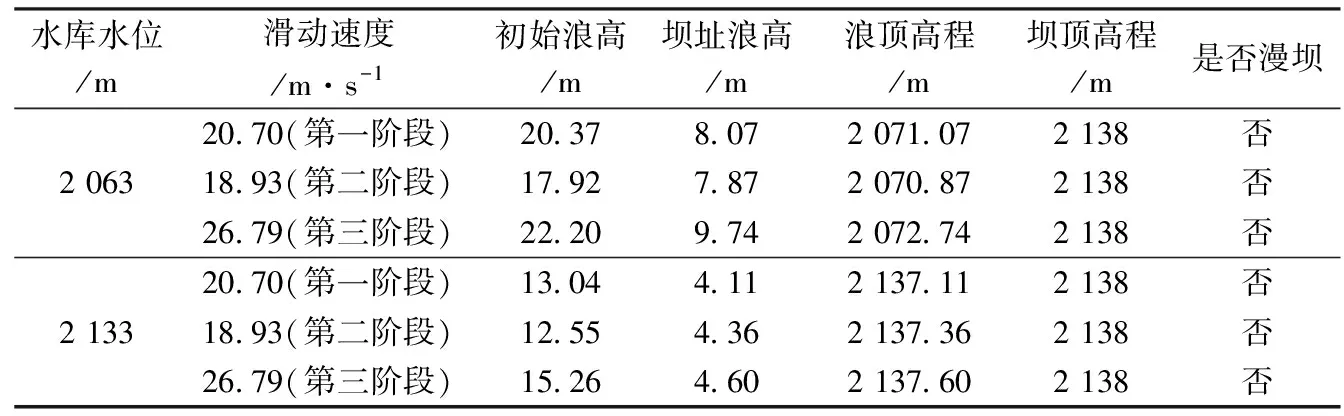
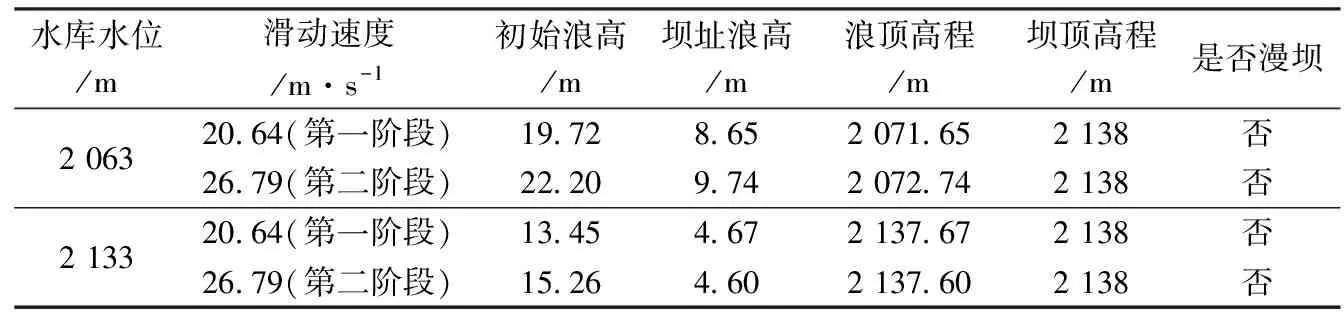

4 计算结果分析
5 结束语
