基于小波去噪的配电网C型行波故障测距
2014-03-19,
,
(四川大学电气信息学院,四川 成都 610065)
0 引 言
统计数据表明,配电网系统发生单相接地故障概率为70%~78%[1],故障发生后能够快速、准确确定故障位置,恢复供电是保障电力系统供电可靠性的关键环节。但因配电网结构复杂,分支众多,常导致故障定位非常困难,是国内外尚待解决的难题。目前配电网系统故障定位可分为主动式故障定位方法与被动式故障定位方法两大类。
主动式故障定位方法是在线路故障发生后向系统注入特定信号,根据相应的定位原理确定故障位置;被动式故障定位方法则是利用线路故障前后线路本身电压、电流等信号特征的变化设计定位判据确定故障位置。两类方法均是分析测量装置接收到的信号以确定故障位置,因此准确提取故障信息是配电网故障定位的关键[2]。
C型行波法是主动式故障定位中的典型方法[3-6]。它是通过比较线路非故障运行和故障运行时检测端接收到的电压行波测距。该法利用故障点返回的行波波头信息确定故障位置。对于单支路或是简单网络,该法可以达到快速准确测距[8]。然而对于含有多分支的实际配电网系统,分支对信号的衰减和噪声的存在对行波波头提取造成很大困难,而电压行波是一个非平稳变换的、具有突变性质的信号[3],小波去噪可以将高频范围内的噪声去除。利用小波对检测端接收到的信号进行去噪处理,在一定程度上减弱了噪声对故障行波波头提取的干扰。
1 行波折射与反射
行波是某一物理量的空间分布随着时间的推移,沿着某一介质行进形成且传播方向为无限的一种形态。行波在波阻抗不连续处会发生折射和反射。对输配电线路而言,电压行波和电流行波的比值为线路的波阻抗,线路的波阻抗与线路本身的结构与绝缘介质及导体材料有关,而与线路长短无关[4]。

图1 行波在波阻抗不连续点的折反射过程
图1中O点为线路波阻抗不连续点,当入射波Ui到达O点时发生反射和折射,产生反射波Ur和折射波Uj。设O点左侧线路波阻抗为Z1,右侧线路波阻抗为Z2。则有[2]
Ur=(Z2-Z1)/(Z2+Z1)·Ui=αUi
(1)
Uj=2Z2/(Z2+Z1)·Ui=βUi
(2)
式中,α=(Z2-Z1)/(Z2+Z1)为电压行波反射系数;β=2Z2/(Z2+Z1)为电压行波折射系数。
2 C型行波故障定位原理
对于C型行波定位法,如何从检测端接收到的行波信号中辨识故障行波波头对于测距的准确度是非常关键的。故障点与检测端之间的距离、故障点所在线路的区段依赖于行波波头辨识的准确度。
先借用图2所示的简单线路介绍C 型行波测距原理,M为母线端,F点为故障点,线路发生故障后,从检测端(M点)注入高压脉冲信号作为检测信号,检测信号遇到故障点发生反射,反射波返回到检测端,检测端利用接收到的故障点反射行波测距。

图2 C型行波原理示意图
若记信号注入时刻为起始时刻,Δt表示从信号注入时刻到故障点反射信号的波头返回注入端的时间差;S表示故障距离;v表示波速[8],则C型行波测距原理用公式描述如下。
S=1/2 Δt·v
(3)
由行波传播特性可知,行波会在故障点和所有分支点来回反射和折射,至能量衰减为零。为便于讨论,定义故障点首次返回检测端的反射行波为故障点反射波,分支点首次返回检测端的反射行波为节点反射波,检测端接收到的其他信号称为杂波。换句话讲,检测端接收到的信号为故障点反射波、节点反射波和杂波的叠加。为了提取故障点反射波,C型行波法通常采取以下两种方式:一种是在故障后分别向故障相和非故障相注入高压直流脉冲,在检测端得到线路故障和非故障运行两组波形数据,将数据相减得到测量信号,由此提取故障信息;一种是在系统未发生故障前分别向每相注入高压直流脉冲信号得到每相非故障运行数据,线路发生故障后向故障相注入相同的高压直流脉冲信号得到故障信号,将故障相故障和非故障运行得到的两组数据相减得到测量信号,由此提取故障信息。这两种方法原理相同,下面以第1种方式为例讨论。

图3 故障测距仿真拓补图
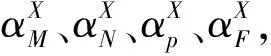

综上所述,在如下时刻检测端接收到节点反射波为

(4)
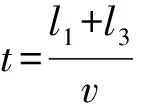
综上所述,在如下时刻检测端接收到节点反射波为

(5)
用C(t)表示线路中行波在各节点往返多次产生的杂波信号,由于节点对信号的衰减作用,杂波信号能量较小,对故障点反射波的 提 取 无 影 响。用e(t)表示实际线路中噪声信号,为便于表示,假设线路波阻抗相同,那么节点的正向电压行波折射系数等于反向电压折射系数,将式(5)、式(4)得到测量信号D(t)为
(6)

(7)
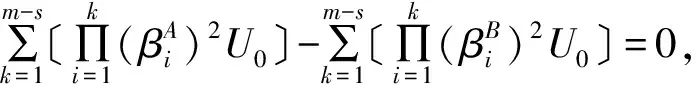
(8)
由上述分析可知:故障点的位置只影响故障点所在支路之后分支点的节点特征波,对于故障点所在支路之前分支点和其他支路的节点反射波无影响。当线路发生故障后,从检测端分别向故障相和非故障相注入同样的脉冲电压,得到线路故障和非故障情况下的反射波两组数据,对比线路故障运行和非故障运行两组波形得到的测量信号,测量信号中波形第一个突变点必为故障点反射波。
3 小波去噪
以上讨论都是在理想情况下进行的,即没有考虑实际线路总是或多或少存在白噪声的影响,噪声的存在将对故障行波波头的准确提取产生影响,外加分支对信号的衰减作用,故障点反射波有可能完全湮没在噪声信号当中,检测端若不能将故障点反射波从噪声中有效的分离出来,将直接导致故障定位失败。
图4为线路中加入信噪比为40 dB的高斯白噪声的仿真波形。其中实线为C行波算法在没有加入噪声时的理想波形,虚线为加入噪声后的波形。图中可以明显看出,加噪后的波形杂乱无章,故障点特征行波完全湮没在噪声信号中,按照C行波算法,故障点的特征行波应为局部放大图5中的第一个负向突变点0.000 014 s处,根据测距原理测得故障距离为

=1.50 km
这和故障点距离检测端20 km,误差过大。因此受到噪声的干扰,无法正确识别故障点反射波,无法测出故障点的距离,因此在提取故障信号之前需要去噪处理。

图4 信噪比40 dB噪声反射行波
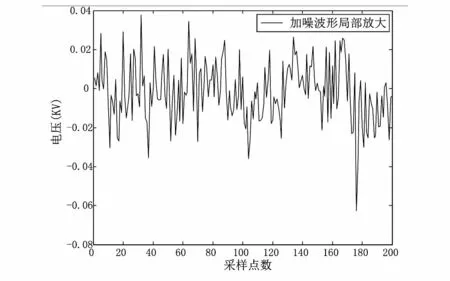
图5 信噪比40 dB测量信号局部图
利用小波进行去噪[8]。小波去噪是将需要被提取的信号按照频率大小对其进行小波分解,利用噪声和信号在频域上的分布不同而完成的。是一个信号滤波问题。传统的傅里叶信号去噪方法直接对信号进行低通或带通滤波,虽然达到去噪效果,但破环了信号细节。而电压行波是一个具有突变性质的信号,需要去噪后还可以很好地保留信号特征,利用小波分析既能将噪声的影响降低,又能保持信号细节信息,实际上是特征提取和低通滤波功能的综合[9]。
设f(t)∈L2(R),ψ(t)为基小波函数,则连续小波变换及其逆变换(重构)的定义为[10]
(9)
(10)

(11)
离散小波变换的系数为

(12)
其重构公式如下所示。
(13)
式中,C为常数,与信号无关。
从以上分析可以看出,小波去噪就是对信号信息进行二频带划分,观察信号在不同频带上的实现,从而实现对反射行波信号的特征提取和去噪。
对于小波基的选择,电压行波是一种非平稳的突变信号,综合考虑时域和频域的紧支撑性和带通滤波性,基于重复实验,经验选择原则,选择db4小波[11]。由于行波信号的小波变换后的系数具有模极大值,且不算尺度变化而改变,而噪声的小波变化随着尺度的增大而迅速衰减,据此可以将噪声和信号分别出来[12]。图6为db4小波五层分解后的波形图。从图中对比可以看出,小波去噪可以将故障信号在一定程度上从原本杂乱无章的信号中提取出来,同时细节信息得以保持。同样根据式(3)选取第一个负向模极大值点0.000 137 s,根据测距原理测得故距离为

=19.95 km
误差为50 m,在误差允许范围内。因此在噪声存在的情况下,经小波分析后可以将故障信号从噪声中有效分解出来,将噪声的存在对C型行波测距算法的影响降低,提高该算法在实际应用中的有效性。

图6 行波信噪比40 dB小波重构波形
4 结 论
采用C型行波测距方法,对于三相平衡的配电网系统,通过比较故障相和非故障相电压行波信号,消除了波阻抗不连续点对故障特征行波的影响。利用小波分析算法对检测端接收到的测量信号进行多尺度分解、重构去噪处理,通过PSACD和MATLAB的仿真验证,在理想条件下算法总体误差控制在50 m,在误差允许范围内。有效地去除了配电网实际运行中噪声的存在对故障行波波头提取的影响,进一步提高C型行波算法在配电网故障测距实际应用中的有效性。
[1] 葛耀中,徐丙垠.利用暂态行波测距的研究[J].电力系统及其自动化学报,1996,8(3):17-22.
[2] 季涛,谭思园,徐丙垠,等.基于波形分析的直流系统接地故障检测新方法 [J].电力系统自动化,2004,28(22):69-72.
[3] 覃剑,葛维春. 影响输电线路行波故障测距精度的主要因素分析 [J].电网技术,2007,31(2)28-36.
[4] 季涛.基于暂态行波的配电线路故障测距研究[D].济南:山东大学,2006.
[5] 骆敬年,颜延纯.基于行波原理线路故障测距的误差分析及解决措施[J].华东电力,2006,34(10)31-33.
[6] 于盛楠,杨以涵,鲍海.基于C型行波法的配电网故障定位的实用研究[J].继电器,2007,35(10):1-4.
[7] 文远芳.高电压技术[M].武汉:华中科技大学出版社,2001.
[8] 张兆宁,董肖红,潘云峰.基于小波变换模极大值去噪方法的改进[J].电力系统及其自动化学报,2005,17(2):9-12.
[9] 胡广书.现代信号处理教程[M].北京:清华大学出版社,1999.
[10] 何书元.应用时间序列分析[M].北京:北京大学出版社,2003:139-143.
[11] 任震.小波分析及其在电力系统中的应用[M].北京:中国电力出版社,2003.
[12] 葛哲学,陈仲生.Matlab时频分析技术及其应用[M].北京:人民邮电出版社,2006.
[13] 董新洲,贺家李,葛耀中,小波变换在行波故障检测中的应用[J].继电器1998,26(5):1-4.
