一种改进的SVC在风电系统霍普夫分岔控制中的应用
2014-03-19,,
,,
(1.西南交通大学电气工程学院,四川 成都 610031;2.四川大学电气信息学院,四川 成都 610065)
0 引 言
系统失稳是一个从稳定状态到分岔状态的过程,而分岔理论是分析非线性动态系统稳定的有力工具[1]。在电力系统中,随着控制参数的变化,易发生分岔现象,而以Hopf为代表的动分岔较以鞍结分岔(saddle node bifurcation,SNB)为代表的静分岔提前发生,故Hopf分岔决定了系统的电压稳定裕度。
风电并入电网后,由于其自身的特性,对电压稳定影响大,需要无功补偿,电力系统中无功补偿装置虽然提高了系统的电压,但也会使系统发生新的分岔现象,降低系统的稳定裕度。
高通滤波器技术已广泛用于Hopf分岔控制[2-3],它能自动跟踪系统的平衡点,而不改变运行点。目前对于SVC的研究,用washout filter对其控制来提高电压稳定的文献相对较少。文献[4]对一个单机无穷大系统运用washout filter对其进行分岔控制,但是没有SVC提供无功补偿。文献[5-6]对一个典型的单机无穷大系统,运用带washout filter控制的SVC对系统进行无功补偿,但是该模型仅对消除Hopf分岔点有效果,而系统电压幅值又变化为系统无SVC提供无功补偿时的幅值。基于以上原因,提出了一种带washout filer控制的SVC,不但能够消除系统的Hopf分岔点,扩大系统的参数变化裕度,还能够提高系统电压的幅值。
1 研究理论和方法
1.1 分岔理论简介[7]
非线性电力系统的动态特性一般用一组微分-代数方程(DAE)来描述为

(1)
式中,x代表微分变量;y代表代数变量;μ代表控制参数。微分方程组描述同步发电机、DFIG、负荷元件的动态特性;代数方程描述电力系统的网络约束方程。
式(1)表示的系统在平衡点(x0,y0,μ0)处满足下列方程组。
(2)
在平衡点(x0,y0,μ0)处,将式(1)两边进行微分变换得
(3)
令A=Dxf(x0,y0);B=Dyf(x0,y0)
C=Dxg(x0,y0);D=Dyg(x0,y)
经过变换,可将式(3)变换为
(4)
令J=(A-BD-1C)。
根据动力学知识,系统的动态稳定性可由雅可比矩阵J的特征值来确定。根据李亚普诺夫稳定性理论,当系统的特征值实部全部为负时,系统稳定。当特征值出现一零特征值时,系统发生SN。系统出现一对共轭特征值时,发生Hopf分岔。
1.2 延拓法[8]
延拓法(连续潮流法)用于追踪系统的平衡解流形,是对系统电压稳定性分析的有力工具。它的基本思想是:从初始点开始,随着参数的变化沿相应的平衡解流形曲线对下一点进行预估和校正,直至勾画出完整的平衡解流形曲线。
每向前追踪一步结束后,便用分岔理论判断系统是否发生分岔,再进行对下一点的追踪。
2 带washout filter控制的SVC设计
washout filter 控制法是一种状态反馈法,通过引入新的变量,把控制器施加到被控系统,控制器多为原系统某一状态变量和washout filter的状态变量构成的多项式。这种控制器不改变原系统的平衡点,控制简单,具有一定的鲁棒性[9],易于实现,可利用较小的控制代价实现非线性系统的分岔控制,可应用于高维系统[3],因此可将该方法用于电力系统的分岔控制中。washout filter 是一种稳定的高通滤波器,对于一维的情况,它有如下的传递函数。
(5)
其中,d为washout filter时间常数的倒数。当d>0时,控制器稳定;d<0时,控制器不稳定。根据现代控制原理,由传递函数写出它的状态方程为

(6)
其输出方程为
μ=g(y,k)
(7)
其中,w为washout filter的状态变量;x为输入的系统变量;y为输出变量;k为控制器的增益;μ为控制器输入到SVC的表达式,是一个关于y和k的函数。当系统稳定时,有w=x/d,y=0,相当于输入变量x被冲洗掉了,因此被称为滤波器法。
这里采用SVC的一阶动态模型,其数学模型如下[11]。
(8)
式中,B为SVC的等值电纳;TSVC为SVC的时间常数;KSVC为SVC的放大倍数;Uref为电压参考值;U7为输入的被控节点电压。
所提出的带washout filter控制的SVC模型为
(9)
式中,μ=k·(U7-d·w),该部分起着消除Hopf分岔点的作用,SVC模型的其他部分起着提高电压幅值的作用。
参数值d和k值的确定参考文献[5]中的方法,在Hopf分岔点处求得系统在带washout filter控制的SVC模型时闭环系统的雅可比矩阵,根据特征值实部为负时,系统稳定,来选取参数值。
3 风电系统模型
3.1 发电机系统模型
同步发电机采用四阶数学模型,模型和参数见文献[11],励磁部分采用一阶数学模型,模型和参数见文献[12]。DFIG的动态模型采用非线性三阶微分方程描述,模型参数见文献 [13]。
3.2 动态负荷模型
采用第一类动态负荷(Walve)模型,参数详细含义见文献[1]。
(11)
3.3 网络约束模型
对于同步发电机节点和非发电机节点的网络约束方程见文献[12],对于DFIG节点,将其处理为一个PQ节点,DFIG注入系统的功率即DFIG与系统的接口为
(15)
4 算例分析
4.1 风电系统描述
这里采用3机9节点系统,简化模型如图1,节点2处为同步发电机,节点3处为DFIG,节点7处接入动态负荷和SVC,节点5、9为恒功率负荷,节点1为系统平衡节点。

图1 含DFIG的电力系统
SVC参数:TSVC=0.6;KSVC=10;Uref=1;d=7;k=72。
4.2 仿真分析
下面就对3机9节点系统在没有SVC进行无功补偿、带washout filter控制的SVC(即文献[5-6]中的SVC模型)、所提出的带washout filter控制的SVC模型分别随动态负荷控制参数Q1变化, 利用延拓法进行分岔仿真分析,U7为节点7 的电压幅值,HP表示Hopf分岔点,SNB表示鞍结分岔点。
4.2.1 无SVC补偿
图2为系统在无SVC提供无功补偿的情况下,系统的QV曲线,系统在Q1=1.186 4处发生Hopf分岔。
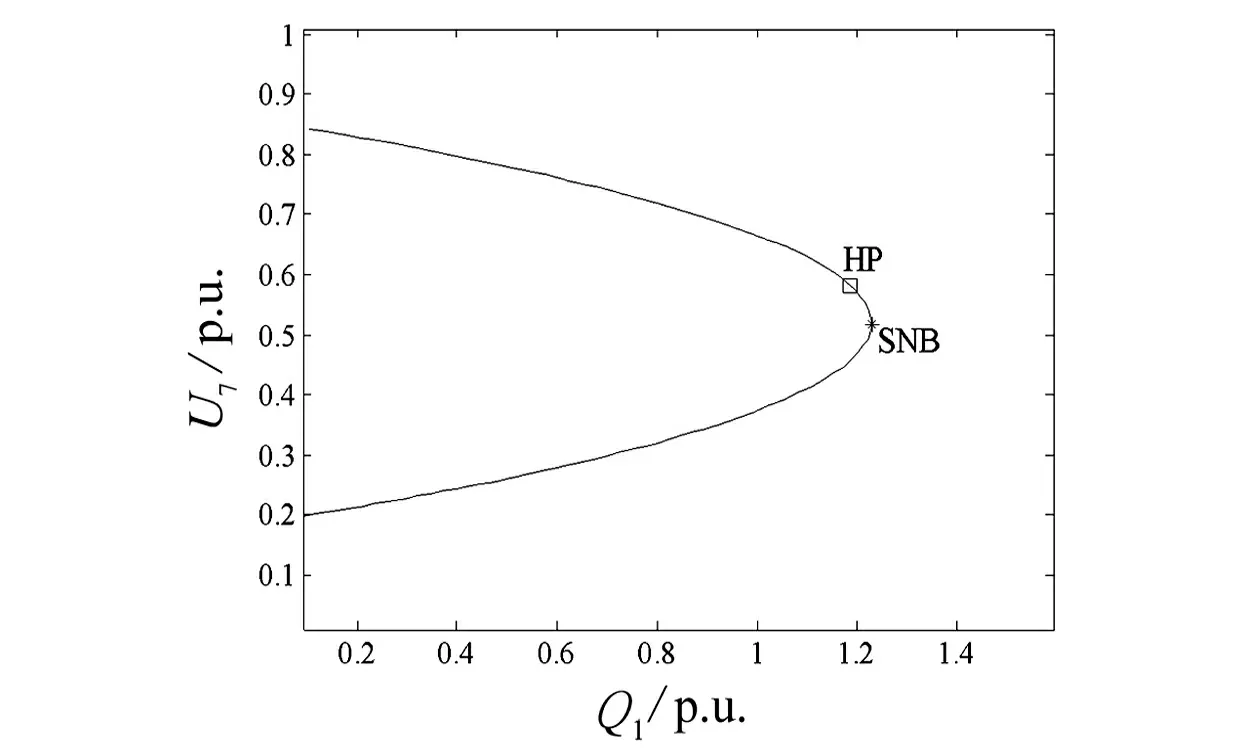
图2 无SVC补偿的QV曲线
4.2.2 不带washout filter控制的SVC分岔分析
图3 为系统在SVC无washout filter控制情况下时的QV曲线,与图2相比,由SVC给系统提供的无功使系统电压幅值得到提高,同时系统在Q1=3.206 2处发生Hopf分岔,比图2中的Q1=1.186 4稳定裕度扩大了。从图4在Hopf分岔点的时域仿真同样可以验证由分岔理论得到的分岔点的正确性。

图3 无washout filter控制的SVC的 QV曲线
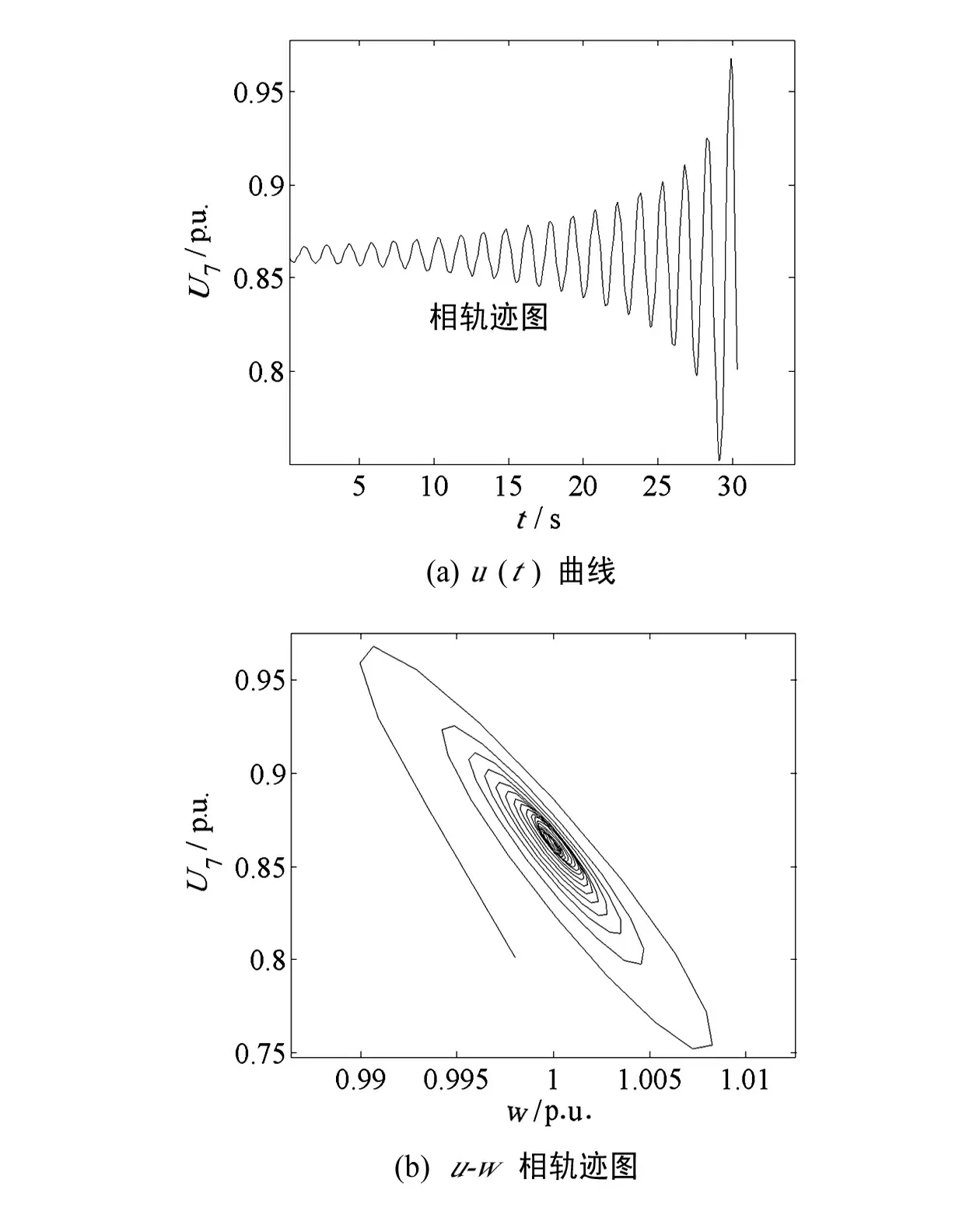
图4 无washout filter 的SVC时的时域仿真
4.2.3 带washout filter控制的SVC
图5为系统在SVC用文献[5-6]提出的washout filter控制模型情况下的QV曲线。由图可得,通过引入该SVC模型确实消除了系统的Hopf 分岔点,但同时和图2相比,两者的QV曲线一样,即在同一控制参数值Q1下的节点电压U7幅值相同,也即是说,该SVC模型下系统的电压幅值降低了,控制参数的稳定裕度变小了。
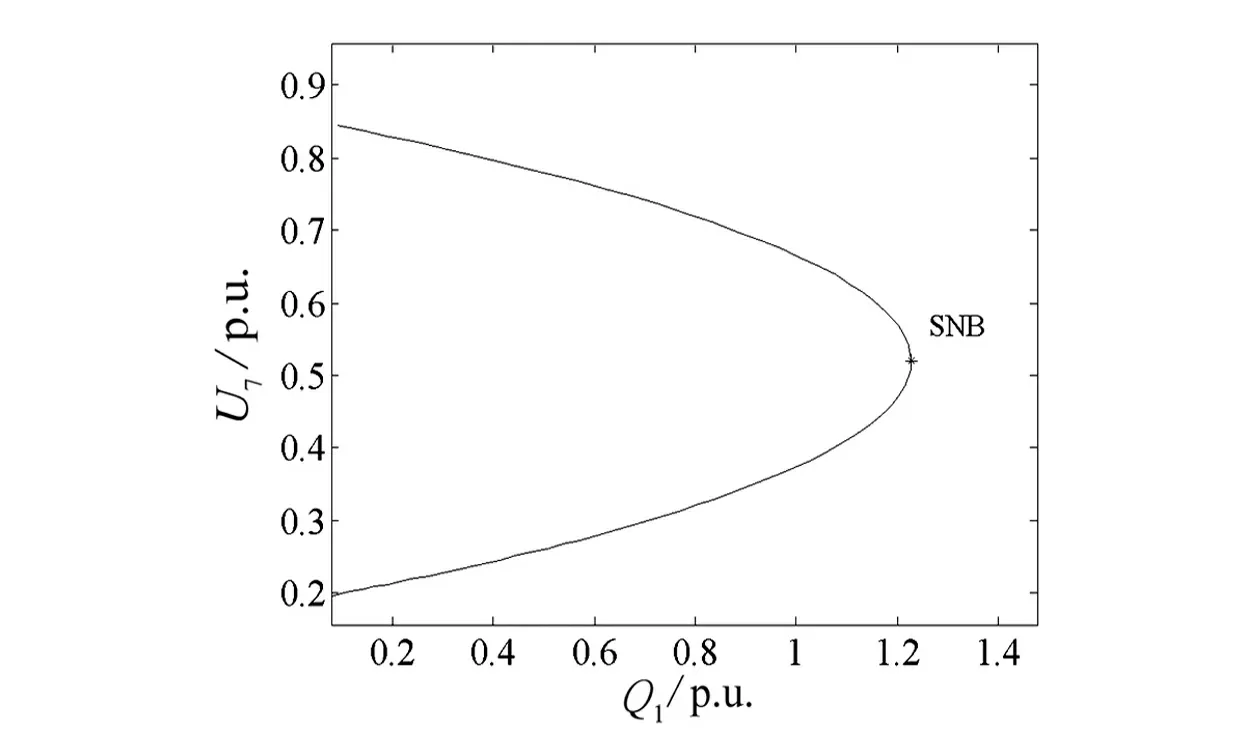
图5 washout filter控制的SVC的 QV曲线

图6 所提出的一种新的washout filter控制的SVC的QV曲线

图7 新的washout filter控制的SVC时系统的时域仿真
4.2.4 带washoutfilter控制的SVC分岔分析
图6为系统在所提出的带washoutfilter控制的SVC模型时的分岔分析。与图3相比,该SVC模型不但保持了原来QV曲线形状,电压幅值并没有降低,同时也消除了系统的Hopf分岔,使系统的稳定裕度得到提高,与图5下的模型仅消除分岔点而系统稳定裕度降低相比,所提出的模型显然更具有优势。在图3中,在Q1=3.206 2,U7=0.862 0处出现Hopf分岔,在该点进行时域仿真,系统不稳定而发散。但在图7中同样参数下,由于消除了分岔点,出现扰动时,系统的电压随时间趋于稳定值,u-w相轨迹趋于稳定收敛,由时域仿真可验证该模型是正确可行的。
5 结 语
当电力系统无功不足时,电压降低,SVC为系统补偿无功可以提高系统电压幅值。前面以动态负荷无功为参数,基于分岔理论和延拓法,首先分析了含双馈感应风电机的电力系统在没有SVC提供无功补偿下的QV曲线,然后分析了SVC在两种控制情况下时系统的QV曲线。在文献[5-6]中washoutfilter控制下的SVC只能消除分岔点,但这是以降低系统电压幅值和稳定裕度为代价的。所提出的washoutfilter控制下的SVC模型,在同样的系统参数下,不但可以消除分岔点,稳定裕度得到提高,还可以提高系统的电压幅值,通过时域仿真验证表明所提出的带washoutfilter控制的SVC模型是正确可行的。
[1]Lerm,A.A.P.MultiparameterBifurcationAnalysisoftheSouthBrazilianPowerSystem[J].IEEETransactionsonPowerSystems,2003,18(2):737-746.
[2]LeHoaNguyen,Keum-ShikHong.AnalysisandControloftheBifurcationinaMorris-LecarNeuronviaaWashoutFilter-AidedDynamicControlLaw[C].11thInternationalConferenceonControl,AutomationandSystems(ICCAS),2011: 342-347.
[3]DongChen,HUAO.Wang.Anti-controlofHopfBifurcationsThroughWashoutFilters[C].Proceedingsofthe37thIEEEConferenceonDecisionandControl,1998(3): 3040 - 3045.
[4] 马幼捷,李小双,周雪松,等.基于高通滤波器技术的电力系统霍普分岔控制[J].电网技术,2011,35(7):76-80.
[5]Saad,M.S.Hassouneh,M.A.Abed,E.H.Edris,A.DelayingInstabilityandVoltageCollapseinPowerSystemsusingSVCswithWashoutFilter-aidedFeedback[C].Proceedingsofthe2005DigitalObjectIdentifierAmericanControlConference, 2005(6): 4357 - 4362.
[6] 安讳春.非线性电力系统分岔控制的研究[D].沈阳:东北大学,2008.
[7] 彭志炜,胡国根,韩祯祥.基于分叉理论的电力系统电压稳定性分析[M].北京:中国电力出版社,2005.
[8] 赵晋泉,张伯明.连续潮流及其在电力系统静态稳定分析中的应用[J].电力系统自动化,2005,29(11):91-96.
[9]CalandririniG,PaoliniE,MoiolaJL.ControllingLimitCyclesandBifurcationinControllingChaosandBifurcationsinEngineeringSystems[C].1999:200-227.
[10]K.N.Srivastava,S.C.Srivastava,P.K.Kalar..ChaoticOscillationinPowerSystemUnderDisburbance[C].InIEE2ndInternationalConferenceonAdvancesinPowerControl,OperationandManagement,HongKong,1993:705-711.
[11] 李康.基于分岔理论的电力系统动态电压稳定性分析[D].成都:西南交通大学,2012.
[12] 顾伟.电力系统最优分岔控制研究[D].南京:东南大学,2006.
[13]K.Elkington,V.KnazkinsandM.Ghandhari.OntheStabilityofPowerSystemsContainingDoublyfedGeneratorbasedGeneration[J].Electr.PowerSystem,2008,78(9):1477-1484.
