基于模糊层次分析的桥梁状态综合评价方法研究
2014-03-19王建民刘君奎张建升
王建民,刘君奎,张建升
(1.北京中交华联科技发展有限公司,北京 100101;2.清华大学,北京 1000841; 3.赤峰市公路管理处,内蒙古赤峰 024000)
0 引言
近年来,随着物联网技术的应用和发展,桥梁结构状态感知与评价技术成为该领域的研究热点之一。相较于传统的桥梁结构安全监测而言,基于物联网的桥梁状态感知与评价更注重传感设备、数据远程传输、感知实时、状态评价客观等方面的综合研究,尤其重要的是引入了物--物感知分析和信息化技术手段,将单个桥梁结构以及布设在桥梁结构上的传感设备通过物联网的相关技术有机的链接组合成一个整体,使得对桥梁结构的状态感知评价由传统的面向特定大型桥梁结构转向适用大量在役中、小跨径桥梁成为可能,也未中、小跨径桥梁结构的安全运营保障以及管养维护提供了一种重要的技术支撑手段。
然而作为以状态感知数据为依据的桥梁结构状态综合评价尚处于起步和待完善阶段。目前多借用传统的评价方法来进行,即可靠度理论法、层次分析法、模糊理论法、遗传算法和神经网络法以及专家系统等[1~6];这些方法往往集中在桥梁各部分构件的检查(测)与单独评价,其在理论上和实践上均有一定的局限性,单纯应用某一种方法进行评价,很难保证评价结果的客观、可靠。为此,进一步改进各种评价理论方法的不足以形成适用于桥梁状态感知的综合评价方法成为了急需解决的课题。
在传统结构状态评价方法中,无论是其可应用性还是理论依据上层次分析方法(The analytic hierarchy process,简称AHP)都具有较明显的优势,且被广泛的进行了应用[7~10];可由于该方法中确定权重的以专家评判构造的判断矩阵往往带有较强的主观性,也即没有充分考虑判断的模糊性,致使评价结果有失客观;实际上,由于影响指标间以及指标对目标的重要性的因素很多,人们对事物的人事也存在多样性并且评价过程存在模糊性,在进行目标评价时指标间的重要程度也必然存在很强的模糊性。
为最大限度地提取专家评判中的模糊信息对桥梁结构状态进行更为客观的评定,有必要将层次分析扩展到模糊数学领域。为此,本文采用模糊层次综合分析法(Fuzzy analytic hierarchy process,简称FAHP)作为桥梁综合状态评价的基本工具,通过模糊数学的方法对判断矩阵的构造进行改进,以给出一种基于模糊层次分析的桥梁状态综合评价方法体系。
1 模糊评价理论基础
模糊评价的基础是模糊集合理论,模糊集合理论被认为是经典集合理论的扩展。经典集合理论的研究对象是具有明确边界的集合,而模糊理论的研究对象是“模糊”集合,其边界是“灰色的”[11,12]。
1.1 模糊集合的概念
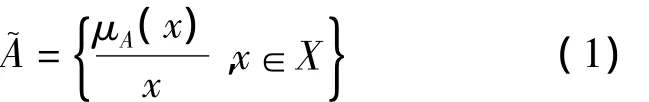
1.2 因素集和评语集
模糊集合定义是设论域X,集合 A,相应的模糊集合记为A~,在论域内,对任意x∈X,x定义常以某种程度μA(x)(μA(x)∈[0,1])属于A~,而非x∈A~或x∉A~;μA(x)称为模糊集合A~的隶属函数,μA(xi)称为xi的隶属度。
一个模糊集 A完全由其隶属函数来刻画。μA(x)值越接近于1,表示x隶属于A的程度越高;μA(x)值越接近于0,表示x隶属于A的程度越低。当μA(x)的值域变为0,1时,μA(x)演化为普遍集合的特征函数,模糊集合A~也就演化为普通集合A,因此可以认为模糊集合是普通集合的一般化。
模糊集合有各种不同的表示方法,一般可表示为:
评价时所要考虑的因素就是这个模糊评价的因素集,即评定时所要考虑的因素就是这个模糊评价的因素集,即U={u1,u2,……un-1,un}。如混凝土桥梁结构按感知指标的属类可分{环境类、荷载类、变形类、应变类、振动响应类},,每个主要构件又可划分为若干项子构件,每个子构件拥有各自的多项因素。
用以确定因素集中每个因素状态评语的集合,即V={v1,v2,……vm-1,vm}。如V={良好、较好、一般、较差、很差}。与评语集V相对应的有评分集G={g1,g2,……gm-1,gm},例如桥梁结构评价中常取G=[100,95,80,60,40][13,14]。
1.3 隶属函数确定方法及隶属矩阵的建立
隶属函数按其形式划分有正态分布型、矩形分布型、梯形分布型、三角分布型、S分布型等,其中以荷兰学者F.J.M.Van Laarhoven和W.Pedrycz提出的三角分布型隶属函数(式(2))在进行结构状态评价之模糊权值分析中最为常用;对于桥梁状态评价,若以得分较高状态较好来表征,则降半梯形隶属函数(式(3))最为适用[15]。
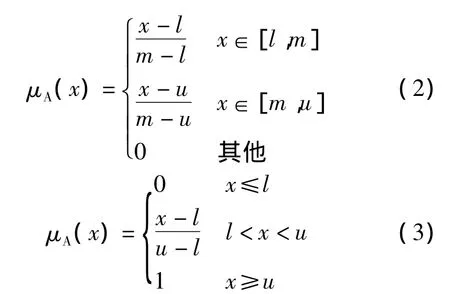
对xi通过隶属度函数求出相应的隶属度,则可以构建起由因素集U(评价指标因素集中的项目数为n)到评语集V(评语集中的项目数为m)的隶属度矩阵R,记为

式中,R中元素rij表示U中第i个因素相对于第j个评价的隶属度。
1.4 因素权重
在综合评价中,权重问题十分重要,只有权重分配合理,才能正确地进行综合评价;设w={w1,w2,……,wn}是U的一个模糊子集的权重向量,它反应各因素的重要性程度,称为因素的权重。在本文中权重的确定将采用下节予以详述。
1.5 模糊评价集B
考虑各因素的权重以后的评价矩阵要通过模糊矩阵合成运算推求,若以B表示合成运算后的多因素模糊评价集矩阵,则有模糊集B,记为:
2 基于三角模糊数判断阵的权重计算
2.1 构造两两比较判断矩阵
2.1.1 判断标度
在递阶层次结构中,设上一层元素C为准则,所支配的下一层元素为u1,u2,…,un对于准则C相对重要性即权重[11];u1,u2,…,un对于C的重要性无法直接定量,而只能定性,那么确定权重用两两比较方法。其方法是:对于准则C,下一层元素ui和uj哪一个更重要,重要的程度如何,通常按1~9比例标度对重要性程度赋值,下表中列出了1~9标度的含义。
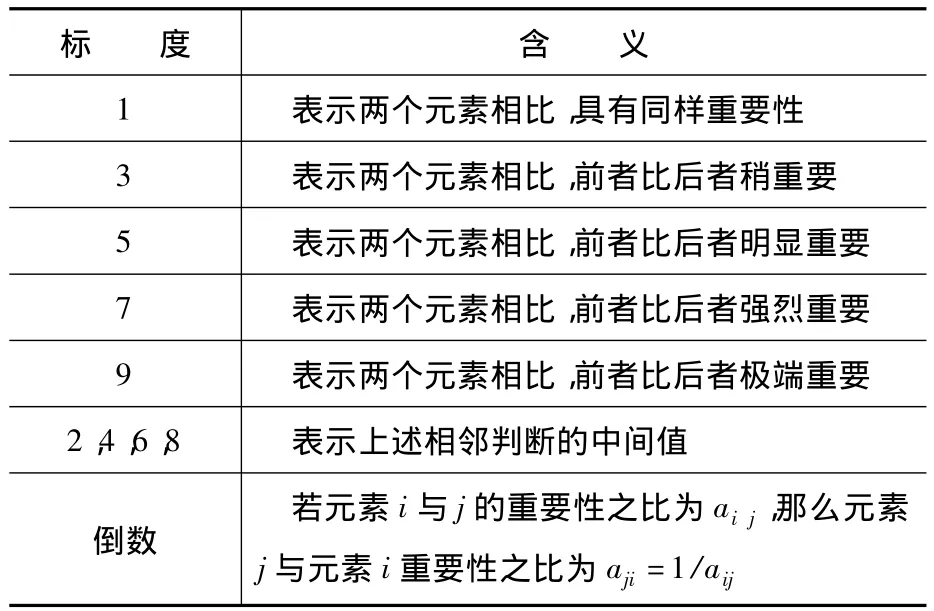
表1 标度的含义
对于准则C,n个元素之间相对重要性的比较得到一个两两比较判断矩阵

其中aij就是元素ui和uj相对于C的重要性的比例标度。
2.1.2 模糊判断矩阵的构造
1)被调查专家利用模糊数来表达他们认为的两因素之间的重要程度或强烈程度,这里假设有3个调查专家,他们对一组指标进行比较,各自得到一个模糊数,分别为(l1,m1,u1),(l2,m2,u2),(l3,m3,u3);
2)将三个模糊数通过下面的方式整合成一个:
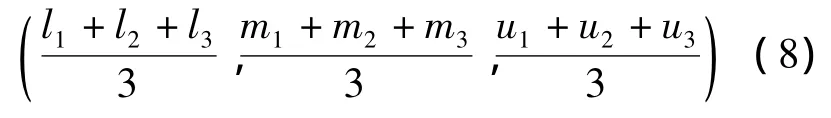
重复以上步骤,直到所有的比较变成一个模糊数。
2.2 计算各个指标的综合权重
2.2.1 第k层指标i的综合模糊值初始权重计算方式
第k层指标i的综合模糊值初始权重计算方式如下:
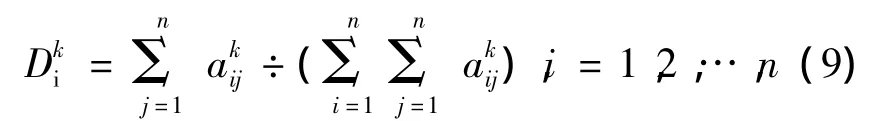
2.2.2 去模糊化
通过模糊数的比较来去模糊化,具体为:
1)M1(l1,m1,u1)和M2(l2,m2,u2)是三角模糊数。M1>M2的可能度用三角模糊函数为: 2)一个模糊数大于其他K个模糊数的可能度,被定义为:

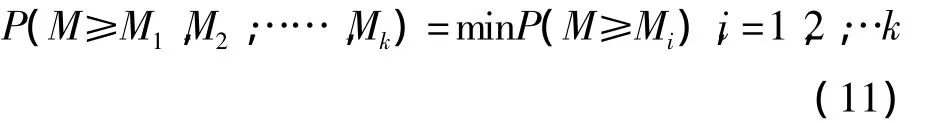
2.2.3 确定最终权重
将所得的权重值标准化,得到各指标的最终权重,设若a、b、c、d为分析得到的四个权重,标准化方式为:

3 模糊数层次分析法综合评价桥梁状态流程及实施步骤
结合桥梁结构状态评价的特点,根据模糊第2节模糊层次分析的内容,采用模糊层次分析法进行桥梁状态综合评价的流程如图1所示。

图1 模糊层次分析方法评定桥梁状态基本流程
桥梁状态评价的具体过程如下:
1)确定指标集
根据感知的指标类别,确定待评价桥梁结构的指标集。
2)确定各指标权重
采用三角模糊数代替传统的标度,得到指标之间的三角模糊判断矩阵,并依次按照式(10)和(11)求出可能度矩阵,最终根据式(12)得到各因素的权重。
3)获得底层指标的评分值
对于所有底层评价指标,按感知数据类型根据相关技术标准及结构计算分析结果计算出底层指标的评分。
4)确定隶属度
本文中各目标的隶属度函数采用降半梯形分布函数来表示,见式(3)。
5)利用模糊变换计算中层指标的模糊评价集
按式(6)计算中层指标的模糊评价集B2,流程图可按照图2所示进行。

图2 一级模糊评价过程
4 算例
某公路钢筋混凝土梁桥,在进行状态评价时,评价层次划分为3个层次,顶层为桥梁整体工作状态层、中间层为反映工作状态的四个因素,因而因素集U={变形,应力,振动响应,环境};评语集V={良好、较好、较差、坏的、危险}。与评语集V相对应评分集取G=[100,95,80,60,40]。计算中字母的下标前面的数字表示在指标体系中的层数,后面的数字表示在本层中的位置;没有下标的表示是最高层(即第三层的指标)。如Bl,2表示底层指标中第二个指标的模糊评价集;R2,1~3表示中层指标中第一、二、三个指标的隶属度函数。
根据文献[5]采用的王光远教授提出的典型函数形式,建立桥梁各因素评价的梯形(降半)分布等级隶属函数,将评分集的分级标准进行模糊化处理,处理后的等级隶属函数图见图3。
底层指标为根据感知的参数的重要程度的评分值及权重,见表2,中间层各因素的权重采用本文的方法进行计算,计算的主要过程如下:
(1)中间层因素权重计算
1)通过对三位相关领域的专家咨询,中间层四个因素(分别记为C1、C2、C3和C4)的模糊判断矩阵,列于表3中,三位被调查专家就各个底层指标在对桥梁状态的评价中的判断是基本一致的。
2)将三个模糊数通过式(8)方式整合成一个,得到模糊矩阵FCM。

图3 状态评价等级隶属图

3)计算各个指标的综合权重。
a)由式(9)计算FCM的C1、C2、C3、C4的初始权重Dc1~Dc4,结果如下:

b)根据式(10)和式(11)将进行去模糊化。
以初始权重Dc1为例,其去模糊化计算如下:
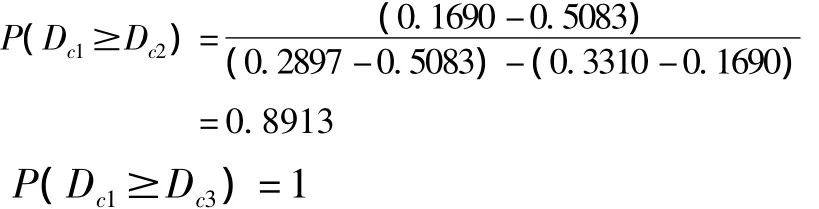
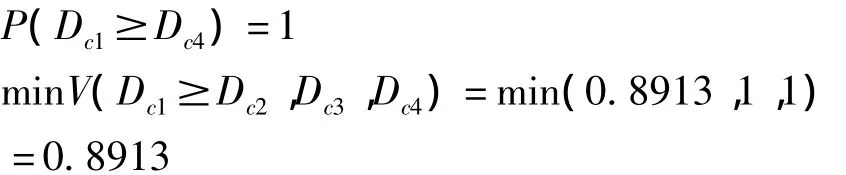
同理,对Dc2、Dc3、Dc4去模糊化得:

c)按式(12)标准化得到最终权重:


表2 梁桥模糊层次分析评价层次划分、底层指标得分及权重
(2)底层指标隶属度矩阵与指标模糊评价集计算
按照式(3)的降半梯形函数,结合图3和底层指标得分值,以作为底层指标的主梁挠度为例,阐明隶属度的计算;该指标得分为83,隶属于“较好”和“一般”之间的模糊区间,对“较好”的隶属度为:
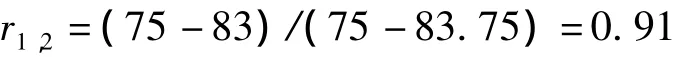
对“一般”的隶属度为:
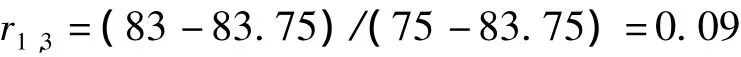
则模糊化向量为(0,0.91,0.09,0,0)。
按同样的计算方法,可得底层指标隶属度矩阵为:

进而得到中层指标的模糊评价集矩阵如下:

则中层权重与中层指标的模糊评价集矩阵相乘则可得到顶层指标的模糊评价矩阵,即
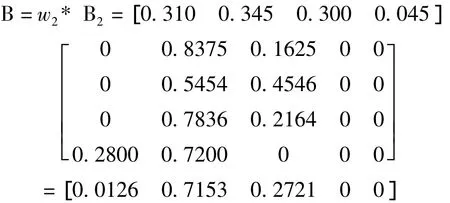
桥梁整体工作状态的评价结果是一个隶属度向量,需要根据最大隶属度邻近判别法即选择模糊评价集中最大值作为最终结果输出;本例评价中隶属度最大值为第二状态,也即该结构整体为“较好”状态、有0.2721偏向“较差”状态、只有0.0126偏向“良好”状态。
整体状态评价汇总见表4,由表中可以看出变形和振动响应这两类感知参数处于“较好”状态,而应力响应参数“较好”和“较差”状态的隶属度基本接近。
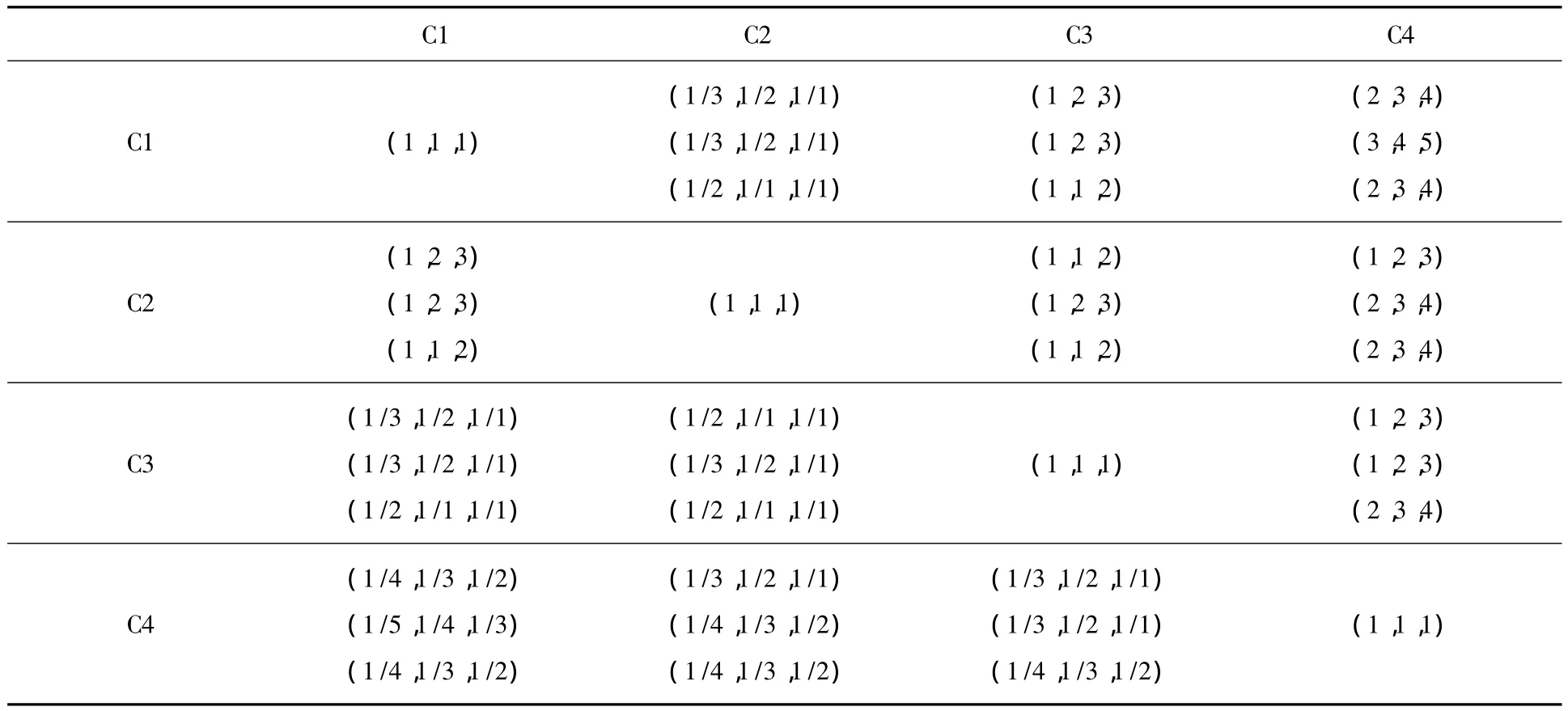
表3 梁桥的的模糊判断矩阵
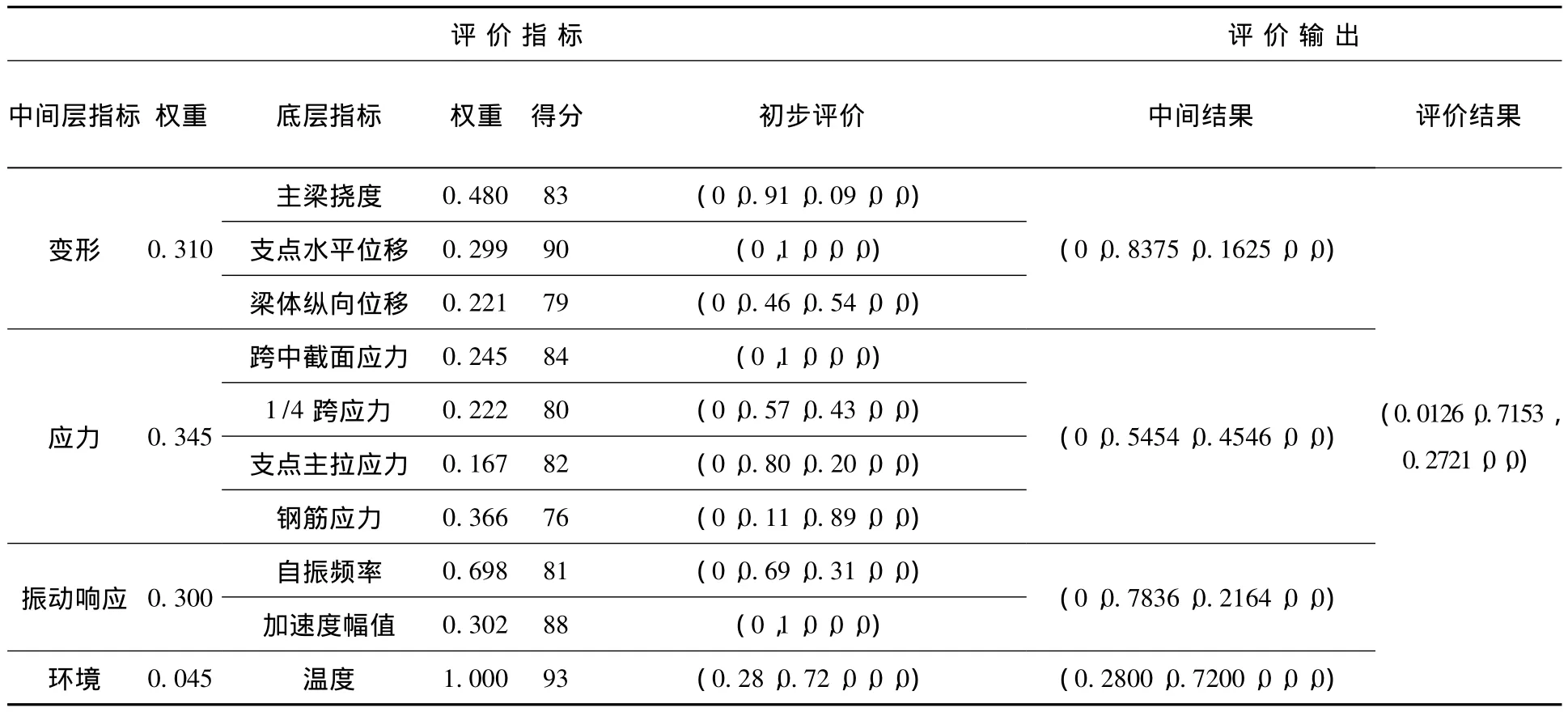
表4 全桥整体状态模糊综合评价汇总表
5 结论
本文以对传统层次分析法评价结构状态中其以专家评判构造判断矩阵确定权重的不足为出发点,综合考虑影响桥梁状态的众多因素在状态评价中存在的模糊性和不确定性,给出了具体权重计算方法、状态评价流程和具体步骤,得到结论如下:
1)将模糊层次分析法应用于以桥梁感知数据为依据的桥梁结构状态综合评价中,不仅能够反映桥梁结构整体客观状态,也可较为全面地考虑影响桥梁状态的主要因素。
2)通过将该方法应用于一公路钢筋混凝土桥梁的状态综合评价,证明了该方法的科学性与实用性,可为桥梁结构的养护管理决策提供技术支持。
[1] 孙光亮.多层次综合评判模型及其应用[J].系统工程,1996,(2):64-67.
[2] 王有志,徐鸿儒,任锋.钢筋混凝土梁式桥的安全性评估系统研究与开发[J].公路交通科技,2002,19(1):51-54.
[3] 赵振宇,徐用懋.模湖理论和神经网络的基础与应用[M].北京:清华大学出版社,1996.
[4] 赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000.
[5] 王永平,张宝银,张树仁.桥梁使用性能模糊评估专家系统[J].中国公路学报,1996,9(2):62-67.
[6] 赵大亮,李爱群.既有公路桥梁评估方法研究现状[J].工程抗震与加固改造.2007,29(1):72-78.
[7] 苏炜,汪箐,吴小柏等.应用层次分析法确定现有建筑价值评估中影响因素的权重[J].河南科学,1999,17(2): 200-204.
[8] 张永清,冯忠居.用层次分析法评价桥梁的安全性[J].西安公路交通大学学报.2001,(07):52-56.
[9] 兰海,史家钧.灰色关联分析与变权综合法在桥梁评估中的应用[J].同济大学学报.2001,29(1):50-54.
[10] 仲伟秋,贡金鑫,赵国藩.钢筋混凝土构件质量综合评判的变权模型[J].哈尔滨工业大学学报,2003,(12):1452-1454.
[11] 李海涛.模糊评判与灰色理论在桥梁建设方案优选中的应用研究[D].合肥:合肥工业大学,2006.
[12] 曾小刚,肖盛燮.模糊综合评判法在旧桥加固方案优选中的应用[J].重庆交通学院学报,2003,22(4):l-4.
[13] 公路养护质量检查评定标准(JTJ075-94).北京:人民交通出版社,1994.
[14] 公路养护技术规范(JTJ073-96).北京:人民交通出版社,1996.
[15] 汪培庄,李洪兴,模糊系统理论与模糊计算机[M].北京:科学出版社,1996.
