锥头圆柱体高速入水空泡数值模拟

马庆鹏 魏英杰 王 聪 曹 伟

(哈尔滨工业大学 航天学院，哈尔滨 150001)

航行体以一定的初速度穿越气水界面进入水中这一过程称之为入水过程.关于入水问题的研究，最早可以追溯到19世纪末，A.M.Worthington和 R.S.Cole［1］利用高速闪光相机、玻璃水槽等设备开展了球体垂直入水实验，阐述并分析了球体入水各个阶段的流动现象.二战后，美国海军基于对空投鱼雷研制的需求，召集诸多学者开展了大量的入水实验研究.美国海军军械实验室(NOL)的 D.Gilbarg 和 R.A.Anderson［2］通过实验研究了大气压力对球体入水喷溅和空泡的影响规律，分析了弗劳德数在入水空泡和喷溅模拟中的影响.A.May 和 J.C.Woodhull［3－5］在此基础上开展了大量的球体及锥体、圆盘等轴对称航行体的入水实验，得到了入水空泡的发展规律以及入水过程的流体动力、入水弹道以及阻力系数等实验数据.公开文献显示，这一阶段的入水实验大多以低速(小于空气中声速)为主.在高速入水方面，1946年普林斯顿大学的 E.N.Harvey和 J.H.Mc-Millen［6］在美国国防研究委员会的报告中研究了钢制球体在约243～914m/s速度范围内的入水问题，并通过实验观察到了入水时产生的弹性激波.在此之后，公开文献没有400m/s以上入水速度的实验开展.在理论研究方面，M.Lee等人［7］从能量守恒的角度，建立了结构入水过程能量转换方程，得到了空泡半径及空泡壁面扩张速度的表达式，在此基础上求解了球体以500m/s初始速度入水的空泡形态及扩张速度.

国内，何春涛、王聪等［8－9］开展了锥头圆柱体在2～56m/s范围内垂直、倾斜入水的模型实验，研究了入水空泡生成、发展和闭合流动过程以及空泡稳定性，并分析了初始速度对空泡闭合方式和形态的影响.同时对低速入水问题开展了相关的数值模拟研究，分析了空泡内的压强分布及对空泡形态、闭合方式的影响.

综上所述，国内外对于入水问题的实验及数值模拟研究大多为低速状态(低于空气中声速)下，对于高速入水的研究很少.本文采用有限体积法和流体体积法(VOF，Volume of Fluid)多相流模型，考虑入水过程的空化及湍流现象，对半锥角为63.5°的锥头圆柱体高速状态下垂直自由入水问题开展了数值计算研究，并将计算结果与文献中基于能量守恒的求解结果进行对比，验证了本文数值计算方法的合理性.进一步开展不同初始速度下的数值计算，分析了入水空泡的生成、发展过程及流场压力分布规律.

1 数学模型

1.1 流体动力学控制方程

本文数值计算假设流体介质为不可压缩，且忽略流体黏性产生的热传导效应，即不求解能量方程，同时不考虑航行体在空气中以超声速运动产生的脱体激波对航行体姿态及水域的影响.VOF多相流模型将多相流体看作单一的流体介质混合物，针对本文所求解的水、空气及水蒸气三相流动问题，分别用 αl，αg，αv表示水、空气和水蒸气的体积分数，在整个流场的任一区域，三者满足关系式:αl+αg+αv=1.

混合流体介质的连续性方程:

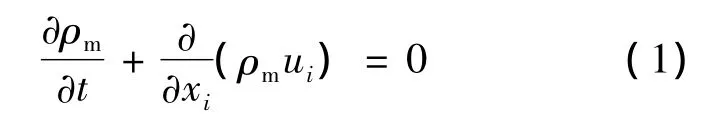
混合相的动量守恒方程为

其中，ui为速度分量;ρm=(1 － αg－ αv)ρl+αgρg+αvρv代表混合介质密度;μm=(1 － αg－αv)μl+ αgμg+ αvμv代表混合介质的动力黏性系数;μt= ρmCμk2/ε 为湍流粘性系数.

1.2 空化及湍流模型

空化是入水问题最重要的流动现象之一，本文采用Schnerr and Sauer空化模型计算液态水的空化问题，该模型的守恒方程基于水蒸气相建立，水蒸气相的体积控制方程为

其中，RB=1 ×10－6m为气核半径;αnuc=5 ×10－4为不可凝结气体体积分数;Fvap=50和Fcond=0.001为经验常数.

湍流是流体的一种随机的非线性运动，也是空化流场的主要特征之一，对于高速入水所涉及的这种强非线性的流动问题，本文采用基于k-ω的SST(Shear Stress Transport)湍流模型进行模拟计算.SST模型综合了常见的k-ε模型边界层外部独立性和k-ω模型近壁稳定性的优点.

2 数值计算

2.1 计算模型及边界条件

由于锥头圆柱体为轴对称体，所以本文数值计算采用二维轴对称模型，航行体半锥角63.5°，柱段直径D=10mm，柱段长度L=50mm.计算域示意图及航行体附近网格划分如图1所示.

图1 计算域及模型表面网格划分示意图

计算域以x轴为对称轴，正向为流场深度增加方向，y轴为流场宽度方向，坐标原点O取航行体顶部所在初始位置.流场空气域高度为32D，流场直径30D，初始时刻锥角顶端距水面距离为2D.航行体径向6D范围内采用三角形网格加密，外场采用四边形网格.其中加密区域近壁面第1层网格高度为D/1000，最外层网格高度为D/40，网格总数量为589752.

2.2 数值计算方法

基于VOF多相流模型采用有限体积法离散、求解流体控制方程，对运动航行体垂直自由入水空泡的发展过程进行数值模拟.压力场与速度场的耦合求解选用PISO算法;压力场的空间离散采用PRESTO!格式;各相体积率离散采用CICSAM格式;综合考虑收敛性与计算时间，对动量方程的离散采用一阶迎风格式.计算过程中，引入动网格技术，利用C++语言编制UDF定义运动区域的运动参数，网格更新方法采用动态层法.为保证求解精度，更新网格高度均为D/40.

3 数值计算结果验证

3.1 基于能量守恒定律的求解方法

图2为入水空泡发展的示意图.文献［7］从能量守恒的角度给出了一种计算入水空泡形态发展规律的方法.

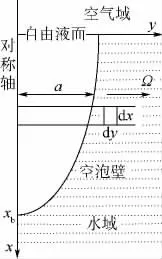
图2 入水空泡示意图

考虑不可压缩流体，忽略入水过程中的热效应，根据牛顿第二定律，可以得到

式中，A0为航行体截面积;Vp为入水速度;ρl为水的密度;)为空化数，其中，p0为参考压强，pv为空化压强;Cdx为阻力系数，其数值采用Sedov［10］得到的公式Cdx=Cd0+σ来确定，Cd0为空化数等于0时的阻力系数.在较低速入水情况下，重力对入水空泡的影响是不能忽略的，但是对于本文计算的500m/s左右的速度区间，可以忽略运动航行体重力的影响，因此，式(4)可以简化为

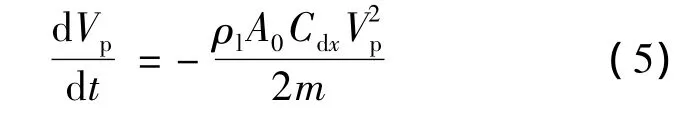
在入水过程中，运动航行体动能的损失率可以表达为

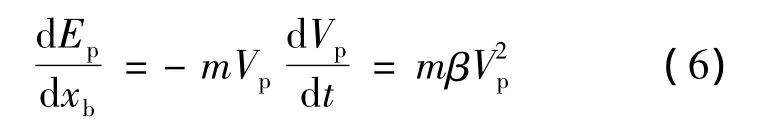
式中，β=ρlA0Cdx/(2m);xb为航行体头部所在位置.

空泡壁面的径向速度可以表示为轴线处点源源强的表达式:

式中ξ为入水深度.

取轴向微小位移d x，排开水的动能为

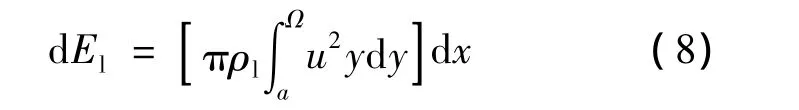
将式(7)代入式(8)可以得到

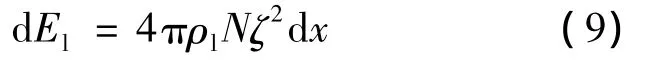
式中N=ln(Ω/a)，其取值一般在15～30之间.文献［11］对于亚音速入水问题研究采用N=15求解，考虑到本文所研究的问题初始入水速度较高，流场横向扰动较大，因此采用N=30求解.

空泡内所积蓄的压力势能可以表示为

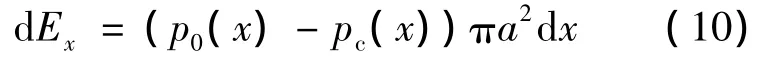
令pg=p0(x)－pc(x)，由于空泡内部为水蒸气和低压气体的混合物，因此，这里假设 pc(x)=3540Pa.

综上所述，根据能量守恒原理，可以得到

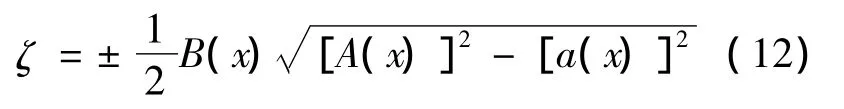
综合式(12)、式(13)，并考虑到当航行体在tb时刻到达深度xb时，空泡半径为D/2，可以得到空泡半径的表达式:

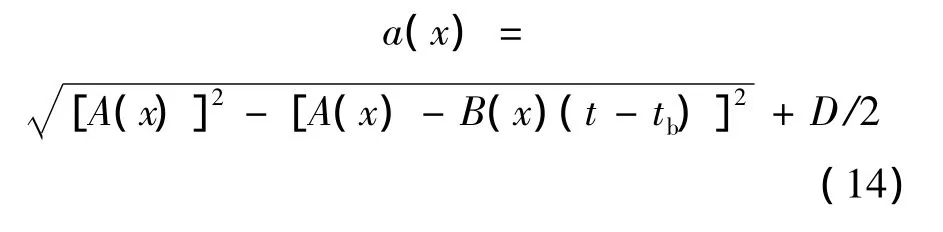
在该表达式右侧，只有一个未知量Vp，且可以通过求解微分方程(5)得到，因此，对于给定的时间t，便可以得到该时刻各深度的空泡半径，当d t足够小时，根据各深度空泡半径便可以描绘出空泡轮廓.

3.2 数值计算结果验证分析

针对本文计算模型，由式(5)、式(14)分别得到航行体以Vp=500m/s初始速度垂直入水的速度衰减曲线及空泡扩张过程.其中，对于半锥角63.5°的 锥 体，Cd0=0.637［12］;水 的 密 度 为998.2 kg/m3;航行体材料为合金铝，密度为2700 kg/m3.采用相同的边界条件开展数值计算.

图3为2种方法得到的入水过程速度衰减曲线，可以看出，数值计算结果与理论解具有较高的一致性.

图3 入水速度变化数值计算与理论结果对比

取入水深度分别为2D，4D，6D和10D这4种情况下的空泡轮廓，如图4所示.

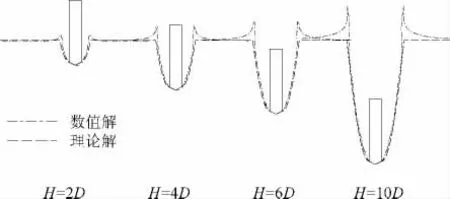
图4 入水空泡轮廓数值计算与理论结果对比

由图4可以看出，2种方法得到的空泡轮廓基本一致，具有较好的一致性.但是由于理论计算没有考虑入水过程的液面波动及入水喷溅等因素，因此在自由液面以上，二者有较为明显的差别.此外，从图4中可以看出数值计算得到的空泡半径略小于理论解，这是由于理论方法没有考虑水横向扩张时的黏性阻力.进一步分析在自由液面处2种算法得到的空泡半径误差，如表1所示.

表1 自由液面处空泡半径误差

由表1可知，在航行体入水初期，空泡半径误差较大，随着入水深度的增加，误差逐渐减小，这是因为在入水初期，流场的运动较为复杂，尤其是自由液面处会产生水面抬升及喷溅等现象，这一时期流体与结构之间互相作用力也尤为复杂.另一方面，在实际入水过程中，入水喷溅在表面张力、大气压力等因素的作用下会呈现向轴线收缩的趋势，进而带动自由液面处空泡口的收缩，而理论方法并未考虑这一点，因此在空泡口处的误差要明显大于远离自由液面处.

通过以上分析和对比验证，可以看出本文采用的数值计算方法能够较好地模拟入水运动参数及空泡的发展过程，其计算结果是可信的.在此基础上，开展不同初始速度条件下，航行体自由垂直入水空泡形态发展规律的数值计算研究.

4 高速入水空泡发展规律研究

4.1 高速入水空泡发展分析

对锥头圆柱体以600m/s初始速度自由垂直入水问题开展数值模拟计算，分析其运动参数、空泡形态、入水空化及流体动力等发展规律.

图5给出了航行体入水后的速度及入水深度的变化规律.可以看出，其速度由600m/s衰减到约150m/s仅运动2ms，在这段时间内，航行体共在水中前行约55D的距离.这表明，航行体在入水初期受到阻力非常大.

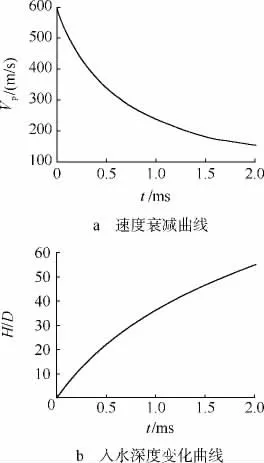
图5 600m/s初始速度入水运动参数变化曲线

提取不同时刻对称轴及航行体表面的压力，取全局坐标系，得到不同时刻的压力曲线，如图6所示.

由图6可以看出，压力峰值出现在航行体头部，不同时刻压力峰值的推移表征了航行体入水深度的变化.可以看出，在航行体触水后，头部流场压力可达到大气压的千倍量级，且在头部顶点处最大.随着入水深度的增大，航行体速度迅速降低，压力峰值也逐渐下降，但在2ms内依然保持较高的水平.这表明在高速入水的前期，航行体将持续受到较高冲击载荷的作用，这对入水结构安全性的设计提出了较高的要求.

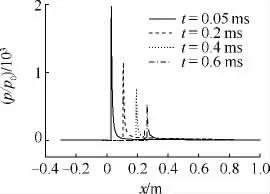
图6 对称轴及航行体表面压力分布曲线

入水空泡的形成与尾端流场的压力密切相关，根据伯努利方程，当航行体高速穿过水域，在排开水的同时亦在接触面附近形成低压区，由此产生空化.提取上述时刻尾端流场对称轴上的压力，如图7所示，其中在0.1ms时刻，航行体尾端尚未到达自由液面处.

图7 航行体尾端流场压力分布曲线

图8给出了空泡发展过程中水蒸气相和空气相的体积分数云图.

图8 入水过程水蒸气及空气相分布体积分数云图

结合图7、图8，由压力曲线可以看出，在航行体完全入水前，尾端空气域压力有一个明显的先上升后下降的过程，这是由于航行体在空气中超音速运动时在尾部流场产生的压力波动.由图8可以看出，在入水初期，空泡内即出现空化现象，航行体排开前端水域后，在空泡壁及靠近自由液面位置产生了大量水蒸气.在空泡扩张阶段，随着入水空泡的生长，空泡内水蒸气不断增多并与空泡内空气混合，阻止了空气从空泡口向空泡前端的运动，此时空泡前端主要由水蒸气和少量的空气混合组成，空泡内部压力迅速降为饱和蒸气压，并产生了零散分布的压力峰值.

4.2 初始速度影响分析

考虑航行体以V1=400m/s，V2=500m/s以及V3=600m/s3种初始速度垂直自由入水，开展入水空泡发展规律的数值模拟研究.

图9给出了不同初始速度入水过程中，空泡最大无量纲直径(Dc/D)随时间的变化规律.

图9 不同入水速度下最大空泡直径变化曲线

由图9可以看出，速度较高时，最大空泡直径更大，随着航行体速度的降低，空泡直径的扩张速度逐渐放缓.这一规律完全符合能量守恒原理，在速度较高时，周围流场可以获得较大的动能向四周运动，因此高速时的空泡直径更大;流体周向运动的过程中，动能逐渐转化为附近流体介质的压力势能，其扩张速度也就随之下降，当扩张速度降为零时便开始反向运动，进而导致空泡的闭合或溃灭.

进一步分析3种入水时刻最大空泡直径的相对增长率，如表2所示.

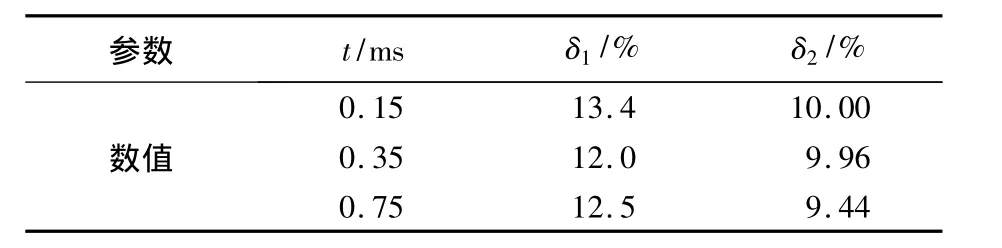
表2 不同时刻最大空泡直径相对增长率

由表2可以看出，各时刻最大空泡直径的增长率都小于速度增长率，这表明流体黏性对空泡扩张有着重要的影响.

图10给出了入水时刻为0.5ms时3种速度下的流场压力曲线.可见，3种状态下压力曲线规律一致，速度越高，压力峰值越大.同时在航行体肩部有明显的压力震荡，可达到参考压力10倍量级，如图10b所示.这表明锥头圆柱体入水过程中，肩部受到流场干扰较大，对于带有一定攻角的入水问题，这一作用极有可能导致弹道的失稳.

图10 不同速度入水状态下对称轴压力分布曲线

5 结论

本文对带有63.5°半锥角的锥头圆柱体高速垂直自由入水问题开展了数值模拟研究.通过对初始速度分别为400，500，600m/s这3种工况下的数值计算结果分析得到以下结论:

1)得到了初始入水速度为500m/s的空泡形态发展规律，并与文献理论计算结果进行了对比，二者具有较好的一致性，验证了本文采用的数值计算方法的正确性;

2)初始速度600m/s条件下，在入水初期航行体头部受到千倍大气压力量级的冲击载荷作用，速度迅速下降，在2ms内衰减至初始速度的25%，同时，强烈的冲击载荷对航行体的结构安全性设计提出了较高的要求;

3)航行体入水后排开周围流体，形成入水空泡，在空泡扩张阶段，空泡直径及长度随入水深度的增大而增大;初始入水速度越高，相同时刻下入水空泡的最大直径越大;

4)在空泡分离点附近，航行体肩部受到较强的随机作用力，对于有攻角的结构入水，极有可能导致其弹道失稳.

References)

［1］ Worthington AM，Cole R S.Impact with a liquid surface studied by the aid of instantaneous photography［J］.Philosophical Transactions of the Royal Society，1900，194(A):175 －200

［2］ Gilbarg D，Anderson R A.Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water［J］.Journal of Applied Physics，1948，9(2):127 － 139

［3］ May A，Woodhull JC.Drag coefficients of steel spheres entering water vertically［J］.Journal of Applied Physics，1948，19(12):1109－1121

［4］ May A，Woodhull JC.The virtual mass of a sphere entering water vertically［J］.Journal of Applied Physics，1950，21(12):1285－1289

［5］ May A.Effect of surface condition of a sphere on its water-entry cavity［J］.Journal of Applied Physics，1951，22(10):1219 －1222

［6］ National Defense Research Committee.Mathematical studies relating to military physical research［R］.AD221604，1946

［7］ Lee M，Longoria R G，Wilson D E.Cavity dynamics in high speed water entry［J］.Physics of Fluids，1997，9(3):540 －550

［8］何春涛，王聪，魏英杰，等.圆柱体垂直入水空泡形态试验研究［J］.北京航空航天大学学报，2012，38(11):1542 －1546 He Chuntao，Wang Cong，Wei Yingjie，et al.Vertical water entry cavity of cylinder body［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(11):1542 － 1546(in Chinese)

［9］王聪，何春涛，权晓波，等.空气压强对垂直入水空泡影响的数值研究［J］.哈尔滨工业大学学报，2012，44(5):14－19 Wang Cong，He Chuntao，Quan Xiaobo，et al.Numerical simulation of the influence of atmospheric pressure on water-cavity formed by cylinder with vertical water-entry［J］.Journal of Harbin Institute of Technolody，2012，44(5):14 －19(in Chinese)

［10］ Sedov L I.Two-dimensional problems in hydrodynamics and aerodynamics［M］.New York:John Wiley ＆ Sons Inc，1965:1－427

［11］ Lundstrom E A.Fluid dynamic analysis of hydraulic ram［R］.NWC TP 5227，1971

［12］ May A.Water entry and the cavity-running behavior of missiles［R］.AD A020429，1975