一般三支链并联机构正解算法
2014-03-19周万勇陈五一
周万勇 陈五一
(北京航空航天大学 机械工程及自动化学院,北京 100191)
刘华东
(北京航空制造工程研究所,北京 100024)
1 问题提出
在少自由度并联机构的家族中,最有应用前景的是空间3自由度并联机构.其中,3RPS机构(图1)最早是由 K.H.Hunt于 1983 年提出[1],由于它能实现2个转动1个移动而得到广泛应用.很多学者对它进行了研究:J.Kim等用Sylvester代数消元法建立了运动学正解[2];孙永生等用牛顿迭代数值法求解正解[3];C.C.Kao等用粒子群算法求解正解[4];黄俊杰等使用遗传算法求3RPS的正解[5].由于球铰的工作空间很小,且制造没有间隙的球铰很困难,所以工程上常用复合球铰代替球铰.由于上述算法都是基于球铰的,直接用于复合球铰的3RPS机构,必然带来系统误差.李新友等基于正交设计分析了3RPS机构的精度[6],但仅考虑了21项误差参数.

图1 3RPS机构原理图
此外,黄真教授等提出了3_5R和3_RPUR机构的构型[7].李仕华等研究了 3_RPRRR机构[8].这些并联机构有一个共同特点——具有3个支链,每个支链5个自由度,其中只有1个自由度是主动自由度,其他4个是被动自由度.
并联机构的支链结构可以用DH法来描述,J.Wang 等用 DH 法建立了 Stewart模型[9].
本文用DH参数表达支链,建立了一般三支链并联机构数学模型.一般的意思是指所有DH参数是任意的.
本文中带复合球铰3RPS机构运动学算法运用了基于对偶四元数的DH法.甘东明、廖启征等曾在解决一般6R机器人运动学算法的过程中应用了此方法[10-11].
2 DH方法的对偶四元数表达
表示刚体位置和姿态的最常用的方法有4×4齐次坐标矩阵、李群SE(3)和对偶四元数3种方法[12].
本文中用对偶四元数表示刚体的位置和姿态,它用8个数表达了齐次变换矩阵用16个数表达的信息,使表达方法更紧凑.用这种方法进行数学处理,降低了问题的复杂度.
对偶四元数是W.K.Clifford于1878年为研究刚体运动群引入[13],表示为


由于刚体仅6个自由度,因此对偶四元数需满足2个约束条件:

四元数部h=b0+b1i+b2j+b3k可以表达刚体的姿态.用对偶四元数表示刚体的位置为
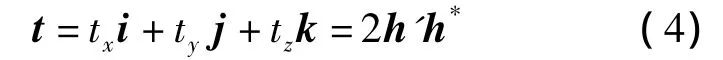
根据对偶四元数乘法:

姿态为h=h1h2,位置为
为了描述空间机构中各个构件之间的相对位置和姿态,J.Denavit等于1955年提出了一种四参数方法[14],即DH方法,被广泛应用于串联机构.连杆i相对连杆i-1的相对关系,用对偶四元数法表达DH方法如下:

式中,Zi=cos(θi/2)+k sin(θi/2)为绕z轴转角;Si=sik为沿 z轴平移;Xi=cos(αi/2)+i sin(αi/2)为绕x轴转角;Ai=aii为沿x轴平移.
在下文中为了表达简洁,式(1)表示对偶四元数用 {(b0,b1,b2,b3),(e0,e1,e2,e3)}.
3 一般三支链并联机构运动学模型
3RPS,3_5R,3_RPUR 和3_RPRRR 等并联机构可以用同一个数学模型表达.它们的运动学模型为

一般三支链并联机构共包括:3个主动驱动参数,75项几何结构常参数,20项未知量,共98个参数.
3RPS,3_5R,3_RPUR 和3_RPRRR 这4种构型主动驱动都在上,在主动驱动锁定的情况下,它们仅仅是DH参数值不同,数学模型和求解方法完全一样.
4 一般三支链并联平台的正解
运动学正解可表达为:已知 sj2(j=1,2,3),求^N.动平台的位置和姿态用对偶四元数表示,包括8个变量:

每个支链包括被动关节转角有4个未知变量θj1,θj3,θj4,θj5,总共有3 个支链,加上动平台 8 个未知变量,正解问题需要求解20个未知变量.
4.1 代数消元处理

支链方程式的左边包括 3 个变量 θj1,θj3,θj4,右边包括 9 个变量 b0,b1,b2,b3,e0,e1,e2,e3θj5.将式(8)左边j支链按对偶四元数乘积展开可得

式中,z(*)的功能是把对偶四元数转换成8维向量;Bj8×8是与支链结构常参数和已知条件sj2有关的8阶可逆矩阵.将式(8)右边j支链按对偶四元数乘积展开可得8维向量函数:

式中 mjk(k=1,2,…,8)是 b0,b1,b2,b3,e0,e1,e2,e3,θj5变量的2次多项式函数.
由式(8)~式(10)可得


可得 yjk(k=1,2,…,8)是以 b0,b1,b2,b3,e0,e1,e2,e3,θj5为变量的2次代数多元多项式函数.
由式(9)可知

三角恒等式:

由式(12)和式(13)计算Groebner基,略去高阶恒等式,可以得到

将式(11)中yjk的2次多元多项式函数代入式(14)~式(22)的9个等式,可得

每个恒等式是9个变量4次的108项代数多项式.每个支链9个等式,3个支链共27个恒等式.通过本节的消元,每个支链消去3个未知量,共消去9个未知量,现在方程组还有11个未知量.
4.2 用高斯牛顿迭代法解多元多项式方程组
一般三支链并联机构的解需要同时满足式(23)的27个方程和动平台对偶四元数的2个约束条件式(2)和式(3),共29个11元多项式方程组.将其表达为29维列向量函数形式:

其中的变量为11维行向量形式:

29个方程多于11元,但从推导过程可知,并不构成矛盾方程组.求解此非线性方程组是非线性最小二乘求解问题,而高斯牛顿迭代法是解此问题的常用方法.
另外,多元多项式方程组一般是多解的,但工程上不需要多解,仅需要一个可行解.故从可行解空间选择一个初始值出发,用高斯牛顿迭代法通过迭代若干次,一定收敛于一个可行解上.
求解过程首先需计算雅可比矩阵J=∂F/∂X.它是29行11列的多项式矩阵.代入初值X0按下式进行迭代:

需指出,变化式(25)可改成LM(Levenberg-Marquard)算法,LM算法比高斯牛顿迭代鲁棒性好,但慢许多.经反复计算验证,本算法可在0.5 s以内完成运算,并且很稳定.
5 算法验证
本文验证对象采用北京航空航天大学和北京航空制造工程研究所联合研制的3RPS并联机构(图2).该机构支链与静平台链接使用R副,与动平台链接使用复合球铰链.由于复合球铰链名义结构参数要求轴与轴垂直相交.但工程实际中做不到0误差.从精度角度看,该机构属于一般三支链并联机构(图3).本文提出的算法可以解决实际结构参数中,距离不为0、角度参数不为90°情况下的正解.
5.1 确定结构参数
首先建立支链坐标系,从静平台到动平台,依次将支链上的构件编号为 1,2,3,4,5,固定在各构件上的局部坐标系分别命名为Oi-xiyizi,简称为坐标系i(i=0,1,…,5).另外分别在动静平台的中心建立坐标系B-xyz和P-uvw,简称为坐标系B和P.按DH方法建立并联机构支链的坐标系,根据坐标系得到支链上各构件参数见表1.3个支链的名义参数是相同的,实际参数是不同的,限于篇幅这里仅以一个支链为例说明.

图2 一般3RPS并联机构样机

图3 一般三支链并联机构原理图

表1 支链上各个构件的名义参数
根据支链中各个坐标系的定义,用对偶四元数做出支链j从坐标系i-1到坐标系i的变换,即为
静平台铰链位置和方向见表2.动平台铰链位置和方向见表3.

表2 静平台铰链在静平台坐标系中的位置和方向

表3 动平台铰链位置在动平台坐标系中的位置和方向
5.2 名义结构参数的算法验证
经典的3RPS反解算法[7]中,认为动平台位姿6个参数中只有3个独立的变量,如γ,β,z.表示动平台位姿的其余3个量α,x,y分别由下面3个公式来确定.动平台位姿确定后,根据两点间距离公式易求得驱动 l1,l2,l3.

应用经典的3RPS反解算法,对本文提出的正解算法进行计算验证.验证的方法如图4所示.

图4 名义结构参数算法验证图
用经典的3RPS反解算法的结果,代入本文用名义参数建立的3RPS正解算法.比较2个算法的动平台位姿,位姿一致即可验证.
经反复验证,本文正解在计算名义参数时的结果时总是与经典3RPS反解算法的动平台位姿一致.
经典的3RPS反解算法事实上只有2个可标定的结构参数,即动平台半径r和定平台半径R.在工程实践中几乎无法应用.
5.3 一般性结构参数的算法验证
下面验证本文拥有78项可标定结构参数的一般三支链并联机构正解算法.
一般三支链并联机构每个支链都可以看成是一个5自由度串联机器人.串联机器人的正解是成熟算法,是一串矩阵的乘积,可以借助串联正解进行算法验证.验证算法对一般性结构参数有效.以支链1为例,验证方法如图5所示.将3个支链的杆长驱动代入到本文的一般3支链正解算法,可得到动平台位姿和所有的被动关节转角.这样每个支链的所有DH参数中的变量都确定了,代入到串联机器人正解算法,计算出由各支链得到的动平台位姿.比对本文算法计算的动平台位姿和支链串联正解算法计算的动平台位姿即可验证.

图5 一般性结构参数算法验证图
用串联机器人正解算法建立3个支链的正解算法,如下式:

根据本文第5.1节的参数可以得到3个支链共6个铰链座的位姿.
工程实际中由于加工和装配的误差,每个支链都是不同的.3个支链具体DH参数见表1~表3.为了表现轴与轴的不相交和3个支链DH参数的独立性,3个支链DH参数故意设置得不一样.支链1上各个构件的DH参数见表4.

表4 支链1上各个构件的DH参数
下面进行计算验证.
将杆长作为算法输入:L1=1 202.79mm;L2=1283.31mm;L3=1223.29mm.
算法得到动平台位姿:

同时可得支链的DH变量:

将DH变量参数代入到串联机器人正解,可得动平台位姿矩阵:

本文算法计算的动平台位姿与3个支链串联机器人算法计算的位姿一致,由于串联机器人的关节角的输入也为本文算法求得,假如本文算法不正确,不可能3个支链用串联机器人正解算法分别计算的动平台位姿是一致的,并且还与本文算法计算的动平台位姿完全一致.因此可以断定本文算法是正确无误的.
6 结论
1)针对一般三支链并联机构,本文采用对偶四元数方法和DH方法,建立了考虑铰链安装位姿参数及所有支链DH参数的一般三支链并联机构正解算法.算法为考虑了并联机构总共78项几何参数及全部DH参数的精确的数学模型.分析这些几何参数对动平台位姿的影响,可用于对一般3支链并联机构的精度分析、精度综合、运动学标定和精确的运动仿真.
2)该算法适用于3条支链共同支撑1个平台,每个支链结构为一般5自由度串联机器人,其中只有1个主动运动副驱动的三支链并联机构.文中使用的方法可以把 3RPS,3_5R,3RPUR,3RPRRR等原来认为不同拓扑结构的并联机构归为一类,用统一的数学模型描述,区别仅在于具体一个支链的DH参数主动变量是转动或是移动;其他的DH结构常量或为零或不为零.
References)
[1] Hunt K H.Structural kinematics of in-parallel-actuated robotarms[J].Journal of Mechanisms Transmissions and Automation in Design,1983,105(4):705 -712
[2] Kim J,Park FC.Direct kinematic analysis of3-RS parallel mechanisms[J].Mechanism and Machine Theory,2001,36(10):1121-1134
[3]孙永生,韩先国,陈五一,等.并联机构大范围收敛高效正解算法[J].计算机集成制造系统,2012,18(5):981 -987 Sun Yongsheng,Han Xianguo,Chen Wuyi,et al.High efficient approach of direct problem with extensive convergence on parallel mechanism[J].Computer Integrated Manufacturing Systems,2012,18(5):981 -987(in Chinese)
[4] Zhan T S,Kao C C.Modified PSO method for robust control of 3RPS parallel manipulators[J].Mathematical Problems in Engineering,2010:302430-1 -25
[5]黄俊杰,赵俊伟.3-PRS并联机构位置正解分析[J].河南理工大学学报:自然科学版,2012,31(4):434 -436,452 Huang Junjie,Zhao Junwei.Research on kinematic forward solution for 3-PRS parallel mechanism[J].Journal of Henan Polytechnic University:Natural Science,2012,31(4):434 - 436,452(in Chinese)
[6]李新友,陈五一,韩先国.基于正交设计的3-RPS并联机构精度分析与综合[J].北京航空航天大学学报,2011,37(8):979-984 Li Xinyou,ChenWuyi,Han Xianguo.Accuracy analysis and synthesis of3-RPS parallel machine based on orthogonal design[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(8):979 -984(in Chinese)
[7]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006:262-268 Huang Zhen,Zhao Yongsheng,Zhao Tieshi.Advanced spatial mechanism[M].Beijing:Higher Education Press,2006:262 -268(in Chinese)
[8] Li SH,Ma N,Ding W H.Kinematic analysis of a novel 3-DOF 3-RPUR translational parallel mechanism[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics,AIM.Piscataway,NJ:IEEE,2008:516 -521
[9] Wang J,Masory O.On the accuracy of a stewart platform,Part1:the effect of manufacturing tolerances[C]//Proceedings of the IEEE International Conference on Robotics and Automation.Piscataway,NJ:IEEE,1993(1):114 -120
[10] Gan D M,Liao Q Z,Wei SM,et al.Dual quaternion-based inverse kinematics of the general spatial 7R mechanism[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2008,222(8):1593-1598
[11]廖启征,倪振松,李洪波,等.四元数的复数形式及其在6R机器人反解中的应用[J].系统科学与数学,2009,24(9):1286-1296 Liao Qizheng,Ni Zhensong,Li Hongbo,et al.An application of dual quaternions on the reverse displacement analysis of6R robots[J].JSys Sci& Math Scis,2009,24(9):1286 - 1296(in Chinese)
[12] Aspragathos N A,Dimitros J K.A comparative study of three methods for robot kinematis[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,1998,28(2):135-145
[13] Clifford W K.Application of Grassmann’s extensive algebra[J].American Journal of Mathematics,1878,1(4):350 -358
[14] Danevit J,Hartenberg R S.A kinematic notation for lower-pair mechanisms based on matrices[J].Trans ASME J of Applied Mechanics,1955,22:215 -221
