消费者价格指数和生产者价格指数相关性研究——基于Copula函数

佘雪锋

（台州经济研究所，浙江 台州 318000）

消费者价格指数和生产者价格指数相关性研究
——基于Copula函数

佘雪锋

（台州经济研究所，浙江 台州 318000）

利用Copula函数，基于2004.1-2012.3的消费者价格指数(CPI)和生产者价格指数(PPI)数据，文章实证分析CPI和PPI的相互关系；通过平方欧式距离检验，认为t-Copula函数是所有Copula函数中对CPI和PPI的拟合程度最优，计算结果表明CPI、PPI存在对称的尾部相关性，两者表现出同时上涨或同时下跌的状态；全国消费者价格指数NCPI、城市消费者价格指数UCPI和农村消费者价格指数RCPI与PPI的尾部相关系数分别为0.4192、0.4560和0.2136，农村相对城市自给自足成分较高和消费结构的差异，PPI对RCPI的影响程度要弱于对UCPI的影响程度。

消费者价格指数；生产者价格指数；Copula函数；消费结构

一、引言

消费者价格指数(CPI)是反映一定时期内城乡居民购买的生活消费品和服务项目价格变动趋势和幅度的指标，与居民日常生活密切相关，能够相对全面地反映消费市场价格的变动；生产者价格指数(PPI)是反映全部工业品出厂价格总水平变动趋势和幅度的指标，是反映工业生产领域的价格水平，包括工业品第一次出售时的出厂价格和企业作为中间投入的原材料、燃料、动力的购进价格。目前这两个指数已成为观察宏观经济运行状况、制订和调整政策的重要参考指标，在每月发布时都会引起政府、学界和百姓的广泛关注和热议，而关于CPI和PPI的相互关系越来越成为研究的热点问题。从理论角度而言，PPI是CPI的先行指标，决定CPI的走势和方向，但是从2008年后我国的CPI和PPI走势出现了明显倒挂现象，即生产者价格指数很长一段时间不向消费者价格指数传导或者反向传导，因此厘清CPI和PPI的传导关系对弄清物价问题具有非常重要的意义。

关于CPI和PPI相互关系的研究文献非常多，具体可以归结为以下三类：

第一类是CPI和PPI之间存在“单向关系”，宋金奇(2008)认为CPI是PPI的一个先行指标，而PPI并不是CPI的先行指标，两者表现为非同步的关系，暗含假定CPI的变动是引起PPI变动的原因；邹炜等(2009)认为PPI是CPI的先行指标，会对CPI产生传导作用，当前PPI的走势会决定后市CPI的大致方向；萧松华(2009)的研究表明，由于生产资料价格指数、生活资料价格指数和原材料、燃料和动力价格指数都引导了CPI变动，是PPI引导了CPI的变动；第二类是CPI和PPI之间存在“双向关系”，徐伟康(2010)在质疑贺力平(2008)一文指出贺文的实证分析存在问题，CPI和PPI在短期和长期内互为对方的格兰杰原因；陈贝等(2008)的分析表明，PPI对CPI有显著的相互传递作用，CPI的快速上涨可能会导致PPI更大程度的上涨；戴芸(2009)认为上游PPI增长将加大下游CPI增长，而CPI的上涨反过来也会推动PPI同方向变化。第三类是CPI和PPI之间存在“复杂关系”或“不确定关系”，陈建奇(2008)认为PPI与CPI没有必然的联系，当前PPI几乎不向CPI传导；贺力平(2008)认为CPI和PPI之间存在复杂的关系，两者的关系总体上是预先不能确定的，有关“谁带动谁”的价格传递关系的观点忽视了问题的复杂性，两个价格指数之间可能存在多种因果关系或非因果关系；王学庆(2009)研究认为CPI与PPI之间只有少部分价格存在间接对应关系，PPI上涨并不意味着CPI上涨；张成思(2010)认为贺文在格兰杰因果检验中没有使用ECM修正价格序列的非平稳问题，因此统计推断结果不够准确，研究表明，PPI对CPI的传导是显著的。至此，对生产者价格指数和消费者价格指数传导方向的争论被推向高潮。

基于分析，上述这些研究暗含假定PPI和CPI之间的关系是线性的，但线性相关性不足以全面完整地刻画变量之间的相关结构(Patton，2006)，而非线性相关性分析模型——Copula函数在分析变量间的相关性时更为稳健，它捕捉到的 Kendall相关系数 τ、Spearman相关系数ρ和尾部相关系数比线性相关关系更接近现实。

文章其余部分结构如下：第一部分定义Copula函数和尾部相关性，第二部分为变量说明及统计描述，第三部分为实证分析和模型评价，最后一部分得出分析结论。

二、Copula函数和相关性定义

Copula函数可以追溯到Sklar(1959)定理，它把多维随机变量的联合分布用一维边际分布连接起来，能很好地刻画变量间非线性、非对称的相关关系。目前，Copula函数广泛应用于风险管理、保险和金融经济学，而在农业经济学领域，Copula模型主要被用于农作物收入保险合同的设计和费率定级。Copula函数能用于构造更符合实际的多元概率分布，而不局限于多维正态分布和t-分布等少数几种概率分布；Copula函数将随机变量的边缘分布和它们之间的相关结构分开研究，边缘分布的选择不受限制（吴娟，2009）。

Slark定理：令随机变量的联合分布 F (x1，x2，…，xp)与各自的边缘分布F(x1)，F(x2)，…，F(xp)存在一个Copula函数C，使得：

如果F(x1)，F(x2)，…，F(xp)连续，则：

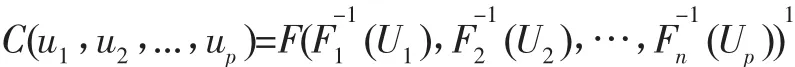
Copula函数就是将多维分布与一维分布联系在一起的函数。根据Copula函数C的密度函数c以及边缘分布F1(·)，F2(·),…，FP(·)得到，p维分布函数F(x1，x2，…，xp)的密度函数：

Copula函数的密度函数c为：

Copula有多种类型，比较常用的为椭圆Copula和阿基米德Copula。

1.椭圆Copula函数

椭圆Copula又可以分为Gaussian Copula函数和t-Copula函数。

（1）Gaussian Copula函数

Gaussian Copula函数源于相关系数矩阵为R的多变量正态分布，分布函数可写成：

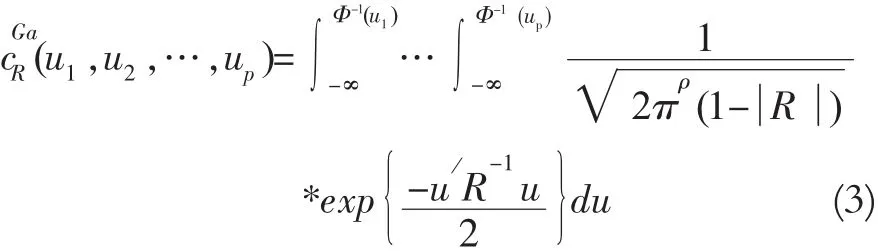
u=(u1，u2，…，up)和Φ-1为单变量标准正态分布累积分布函数的反函数。

（2）t-Copula函数

Gaussian连接函数假定分布的尾部不存在相关性，因此考虑t-连接函数会更适用，通过自由度为v的多变量t分布和相关系数矩阵得到分布函数：为自由度为v的标准单变量t分布函数的反函数，在v趋于无穷时，Gausscian连接函数为t-连接函数的特例。

2.阿基米德Copula函数

令函数φ:[0，1]→[0，∞]是严格的阿基米德Copula生成元，假设反函数φ-1在 [0，∞]是单调函数，φ是连续、递减的函数，满足φ(0)＝∞，φ(1)=0，由此阿基米德Copula被定义为：

（1）Clayton Copula函数

假定生成元函数为：φ(u)=φ-1(u-θ-1)，Clayton Copula被定义为：

密度函数为：

（2）Gumbel Copula函数

假定生成元函数φ(u)=(-logu)θ，Gumbel Copula定义为：

密度函数为：

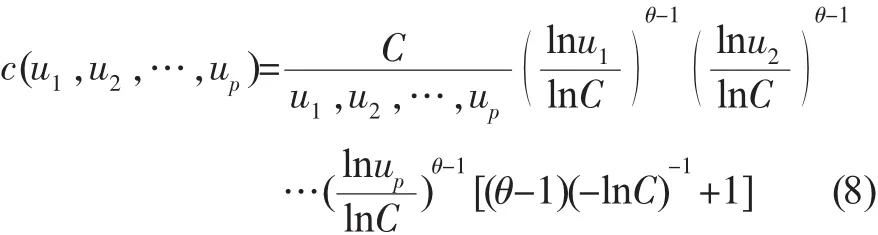
（3）Frank Copula函数

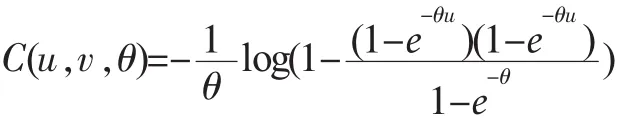
θ=(-∞，0)∪(0，∞)，θ为 Frank Copula的相关参数，θ＞0表示随机变量正相关，θ＜0表示u，v负相关，θ→0表示u，v趋向独立；密度函数为：

3.参数估计

由于选取的Copula函数含有未知参数，因此需要对参数进行估计。

（1）最大似然估计(Maximum Likelihood，ML)

设连续随机变量X，Y的边缘分布函数为F(x；θ1)和G(y；θ2)，边缘密度函数分别为f(x；θ1)和g(x；θ2)， θ1、θ2为边缘分布中的未知参数，样本的对数似然函数：

参数的最大似然估计：

（2）分布估计

通过边缘分布和最大似然估计可以求出 θˆ1，θˆ2估计值：

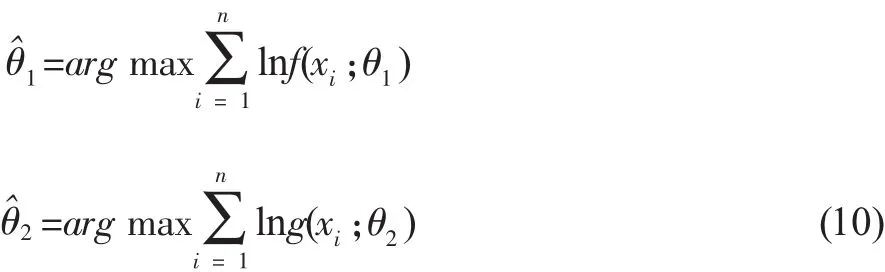
4.相关性估计

（1）Kendall τ和Spearman ρ

基于Copula函数的相关性度量Kendall相关系数τ和Spearman相关系数ρ：

设(x1，y1)连接函数为c(u，v)，可得：

（2）上、下尾相关

尾部相关主要是刻画其在极端情况下的变量之间相互关系的重要指标，定义上尾相关系数：若 λu∈（0，1］， X，Y为上尾相关；若λu=0， X，Y为上尾独立；下尾相关系数：p{Y＜G-1(u)│X＜F-1(u)}，若λL∈（0，1］， X，Y为下尾相关；若λL=0， X，Y为下尾独立，根据定义和推导得到：

对于Gaussian Copula：当-1＜ρ＜1时，λu=0，根据椭圆Copula函数的对称性，当-1＜ρ＜1时，λu=λL=0，即为零尾相关。

Clayton Copula的参数θ和Gumbel Copula的参数与上尾相关系数λU和下尾相关系数λL存在如下关系：

Frank Copula函数具有对称的相关模式，无法捕捉随机变量间非对称的相关关系，并且上下尾相关系数均为零，变量Frank Copula函数尾部是渐进独立的，对上下尾相关性的变化不敏感，难以捕捉尾部相关的变化。

三、变量说明及统计描述

生产者价格指数PPI和消费者价格指数CPI，并将其划分为全国 CPI(National CPI，NCPI)、城市CPI (Urban CPI，UCPI)和农村CPI(Rural CPI)三类，采用月度同比数据，所有数据均来源于国家统计局网站(http: //www.stats.gov.cn)。从图1可见，消费者价格指数和生产者价格指数走势基本相同，表现为“同涨同跌”的状态，即两者或者同时上涨或者同时下跌，只是上升或下降的幅度有差异。将整个样本(2004.1-2012.3)划分为6个阶段，在第1阶段(2004.1-2007.1)、第3阶段(2008.5-2008.10)和第5阶段(2010.1-2011.9)生产者价格指数大于消费者价格指数，在第 2阶段(2007.2-2008.4)和第6阶段(2011.10-2012.3)，生产者价格指数小于消费者价格指数。

表1 变量说明和统计描述

从变量的统计特征看，全国居民消费价格指数(NCPI)和农村居民消费价格指数为右偏接近对称和正态分布，城市居民消费价格指数(UCPI)左偏接近对称和正态分布，而生产者价格指数为左偏、尖峰后尾的非正态分布。

图1 生产者价格指数（PPI）和消费者价格指数（CPI）月度同比

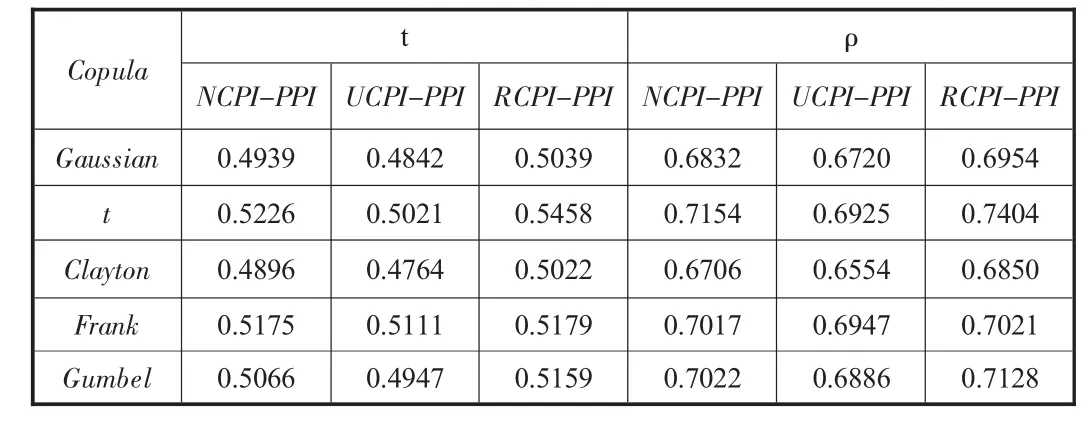
表2 基于Copula函数的CPI与PPI的相关系数

四、实证研究

1.参数和相关系数估计

分别计算出 Gaussian、t、Clayton、Frank和Gumbel五类Copula函数的秩相关系数和参数，结果见表2、表3。

不同的Copula函数对生产者价格指数和消费者价格指数相依程度和相关结构的刻画有所差异，Gaussian和Frank copula的上尾和下尾相关系数均为0，即上、下尾相互独立。

t Copula刻画的NCPI、PPI两个序列的上尾和下尾相关系数均为0.4192，上、下尾存在正向相关并且呈对称分布，两序列表现为“同涨同跌”的状态；Clayton Copula函数捕捉下尾相关的能力比较显著，参数估计也表明，NCPI、PPI序列下尾相关系数为0.7238，两者存在较强的正相关。

t Copula函数刻画的UCPI、PPI两个序列的上尾和下尾相关系数为0.4560，上、下尾存在正向相关关系并且呈对称分布，两序列为“同时上涨或者同时下跌跌”；Clayton Copula函数刻画的NCPI、PPI序列下尾相关系数为0.7178，两者存在较强正相关，上尾相关系数为0，上下尾呈不对称分布，而Gumbel Copula在分布的上尾部变量间具有较强的相关性，相关系数达到0.5625，而在分布的下尾部变量间是渐进独立的。

表3 参数和尾部系数估计

t Copula刻画的RCPI、PPI两个序列的上、下尾存在正向相关且为对称分布，上尾、下尾相关系数为0.2136，相关性较小，两序列也表现出“同时上涨或下跌”的状态；Clayton Copula函数刻画的RCPI、PPI序列下尾相关系数为0.7242，两个序列之间在下尾部存在着较强正相关关系，而Gumbel Copula同样在上尾部存在着较强的正相关关系，相关系数为0.6192，而尾部表现出独立的状态，相关系数为0。

2.模型选取

不同类型的Copula函数在刻画上尾和下尾相关性时具有不同的特点，因此需要对五类Copula函数进行检验，寻找拟合程度最优的Copula函数。从各变量间的边缘分布的二元直方图（如图2(a)、2(b)、2(c)所示，上图代表频数直方图，下图代表频率直方图）可以看出，在尾部分布着较多的点，频数和频率都较高，说明在尾部各变量之间存在相关关系，并且在尾部基本呈对称的分布。

根据上文对变量二元直方图的分析，采用t-Copula拟合变量的相互关系，因为其能捕捉对称的尾部分析。如图3所示，根据t-Copula函数所作的概率密度图和等高线图，t-Copula概率密度图具有较厚的尾部，并且呈对称分布，而等高线图在尾部比较密集并且呈对称分布，因此用 t-Copula函数来拟合NCPIPPI、UCPI-PPI、RCPI-PPI三组变量是恰当的。

同时，为定量地进行模型评价，引入经验Copula函数计算平方欧氏距离，平方欧氏距离的值越小，所对应的Copula函数越能更好地拟合原始数据。设 (xi，yi)，i=1，2，…，n为取自二维总体(X，Y)的样本，记X，Y的经验分布函数分别为Fn(xi)和Gn(yi)，样本经验函数定义为：

其中，I［.］为示性函数，当Fn(xi)≤u时，I［Fn(xi)≤u］=1，否则I［Fn(xi)≤u］=0。有了经验函数，那么我们就可以计算出Gaussian CopulaC^Ga(u，v)、t-CopulaC^t(u，v)、Clayton-CopulaC^Gl(u，v)、Gumbel-CopulaC^Gu(u，v)与经验Copula函数的平方欧氏距离:

图2 (a)NCPI-PPI边缘分布的二元直方图

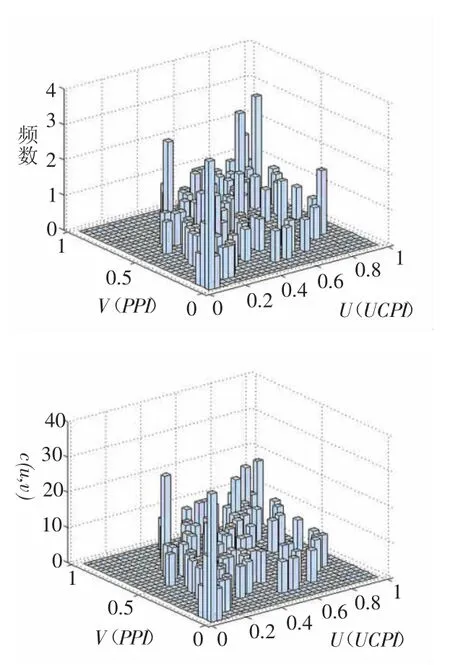
图2 (b)UCPI-PPI边缘分布的二元直方图

由表4可知，在五类Copula函数中，t-Copula函数与经Copula函数的平方欧氏距离最小，所有拟合的NCPI -PPI、UCPI-PPI、RCP I-P PI欧氏平方距离数值分别为：0.0362、0.0356、0.0373，都是拟合程度最好的Copual函数。根据平方欧氏距离标准，函数能够最好地拟合生产者价格指数和消费者价格指数的相关性。

表4 函数的欧氏距离

图2 (c)RCPI-PPI边缘分布的二元直方图

图3 (a)t-Copula概率密度

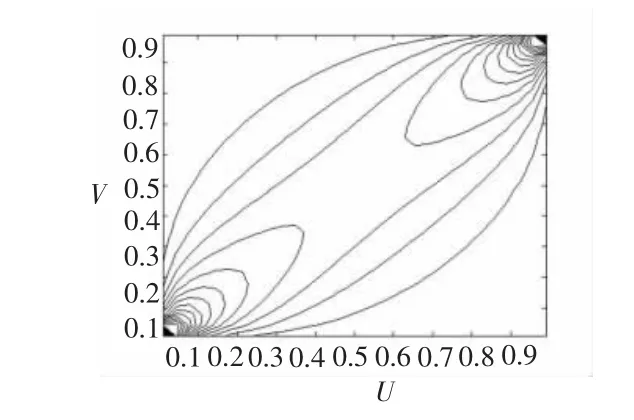
图3 (b)t-Copula等高线

五、研究结论

为捕捉消费者价格指数 CPI与生产者价格指数 PPI之间存在的非对称、非线性的关系，本文引入金融分析中流行的 Copula连接函数刻画这种非对称和非线性，研究表明：CPI和 PPI存在较强的相关性，NCPI-PPI、UCPI-PPI、RCPI-PPI的Kendall系数分别为：0.5226、0.5021、0.5458，Spearman相关系数ρ分别为0.7154、0.6925、0.7404。

通过平方欧式距离检验，认为t-Copula函数是所有Copula函数中对CPI和PPI的拟合程度最优，研究结果认为我国CPI、PPI存在对称的尾部相关性，即两者表现出同时上涨或同时下跌的状态，这与样本期内CPI与PPI的走势表现完全一致；全国消费者价格指数NCPI、城市消费者价格指数UCPI和农村消费者价格指数RCPI与PPI尾部相关系数分别为：0.4192、0.4560和0.2136，NCPI、UCP与PPI的相关程度较高，而RCPI与PPI的相关程度较低，农村相对城市自给自足成分较高及消费结构的差异，PPI对RCPI的影响程度要弱于对UCPI的影响程度。

[1]Demarta，S.，McNEIL，A.J.The t Copula and Related Copulas[J]. International Statistical Review，2005(73)：111-129.

[2]Fermanian J.D.Goodness of Fit Tests for Copulas.Journal of Multivariate Analysis[J].2005，95(1)：119-152.

[3]Genest C，Favre AC.Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask[J].Journal of Hydrologic Engineering，2007，12：347-368.

[4]HU，L.Dependence Patterns Across Financial Markets:A Mixed Copula Approach[J].Applied Financial Economics，2006，10.

[5]Nelson R.B.An Introduction to Copulas[M].New York:Springer，1999.

[6]Pattona.J.Modelling Asymmetric Exchange Rate Dependence[J]. International Economic Review，2006(47)：527-556.

[7]陈建奇.PPI、CPI倒挂与通货膨胀调控—基于非对称供求结构与价格决定机制的实证研究 [J].中国工业经济，2008(11)：24-34.

[8]贺力平，樊纲，胡嘉妮.消费者价格指数与生产者价格指数：谁带动谁？[J].经济研究，2008(11)：16-26.

[9]何光辉.中国CPI与PPI的结构与动态作用机制研究[J].经济科学，2009(4)：15-30.

[10]宋金奇，舒晓惠.PPI与CPI的关系——基于误差修正模型的研究 [J].统计研究，2008(10)：50-51.

[11]宋金奇，文博.PPI与CPI非同步性：理论分析和实证检验 [J].价格理论与实践，2011(3)：43-44.

[12]苏梽芳，蔡经汉.我国CPI与PPI非线性调整的实证解释 [J].中南财经政法大学学报，2010(2)：3-9.

[13]徐伟康.对《消费者价格指数与生产者价格指数：谁带动谁？》一文的质疑 [J].经济研究，2010(5)：139-147，158.

[14]张延群.商品价格指数是消费价格指数的前导变量吗？[J].数量经济技术经济研究，2007(12)：140-149.

（责任编辑：WD）

Study on Dependence between CPI and PPI based on Copula Function——Based on Copula Function

SHE Xue-feng
(Taizhou Institute of Economics，Taizhou Zhejiang 318000，China)

Based on CPI and PPI data from Jan.2004 to Mar.2012，the paper analyzes dependence between CPI and PPI by use of Copula function and finds is the best function to simulate dependence between CPI and PPI.The paper finds that there exists strong symmetric tail dependence between CPI and PPI，that is to say CPI and PPI increase or decrease at the same time. Dependence coefficients between National CPI(NCPI)Urban CPI(UCPI)and Rural CPI and PPI is 0.4192、0.4560、0.2136 respectively，the effect of PPI on RCPI is weaker than that of PPI on UCPI because of relatively higher rural self-sufficiency compared with urban areas.

CPI；PPI；Copula function；The consumption structure

F124.1

A

1004-292X（2014）04-0015-06

2014-01-11

教育部人文社科青年基金项目 （13YJC790079）；浙江省哲社重点研究基地（浙江省产业发展政策研究中心）课题（13JDCY02YB）；浙江省教育厅高职高专院校专业带头人专业领军项目（lj2013144）；浙江省教育厅科研项目（Y201225587）。

佘雪锋 (1979-)，男，湖北随州人，院长，副教授，主要从事国际贸易与产业经济研究。