复合式镗铣加工中心铣削部分空间误差建模研究
2014-03-18曲月舒启林
曲月,舒启林
(沈阳理工大学机械工程学院,辽宁沈阳110159)
随着世界经济的发展和技术进步,高档数控机床已成为世界各国装备制造业的主要工具,是高精度、大批量、多品种机械生产的关键技术装备,是国防安全的战略物资,是汽车和航空航天等工业发展的重要支撑,是降低产品制造成本、保证产品质量、提高产品加工效率和维护市场竞争力的有效手段,其性能、品质和数量已成为衡量国家工业化水平和综合国力的重要标志。
复合式镗铣加工中心是以现有的加工中心技术基础为依托,以军用车辆复杂的箱体结构零件为加工对象,通过组合创新和工艺原理创新,研发出的拥有自主知识产权,具有国内领先、国际先进技术水平的精密复合式镗铣加工中心产品,满足国内军工行业对于高精密箱体类零件的加工需求。复合式镗铣加工中心的总体结构布局是根据军用复杂箱体类零件的结构与精度特点,将龙门式镗铣加工结构与卧式镗铣加工中心结构相结合,创立了电主轴与机械主轴结合的双主轴单龙门同台立卧式布局结构,以确保加工件的位置精度与生产效率。随着加工对象质量要求越来越高,复合式镗铣加工中心的加工精度已成为一个重要研究问题。所以准确、高效地建立该复合镗铣加工中心的空间误差模型是十分有必要的。当今用于建立误差模型的方法有刚体运动学法、BP 神经网络误差建模法[1]、多体系统误差建模法[2]。其中多体系统误差建模法具有通式化、系列化、易于理解等优点。
1 多体系统理论概述
多体系统理论是研究现代机械多体系统的一门经典理论,尤其是在现代科技高速化发展的今天,计算机算法的多种实现为多体理论的运用创造了更加丰富的条件。多体系统是指以一定的连接方式互相关联起来的多个物体所构成的系统。
多体系统理论是由多体系统运动学原理和多体系统动力学原理构成,多体系统运动误差分析是利用多体系统运动学原理对复杂机械系统进行拓扑结构建立并完成其拓扑结构间的关联关系描述。首先需要建立所研究机械系统的低序体阵列,通过低序体阵列说明该系统中的拓扑结构关系;其次是分别在系统中各部件的拓扑结构上设定广义坐标系;最终以4 ×4 阶齐次方阵的形式描述各点在广义坐标系中的变换关系[2]。文中是基于多体系统运动学原理,以复合式镗铣加工中心铣削部分为研究对象,描述了铣削部分多体系统的误差模型建立过程及所需数学公式推导。
2 拓扑结构与低序体阵列
采用多体系统运动学原理对该加工中心铣削部分结构进行误差建模,其核心步骤是如何准确创建出各工作部件之间的拓扑结构。目前可以描述多体系统拓扑结构的通用方法是建立结构体部件的低序体阵列,一般是设基础坐标B 为A0体,任选一体为A1体,然后以远离A1体的方向以增长数列规律去标定每一个结构部件的序号,从该系统的一个分支到另外一个分支,直到全部标定为止[3]。
通常,多体系统内任选体M 的N 阶低序体定义[3]为:

式(1)—(4)称为低序体算子;M 是多体系统中典型体序号;Ln(M)是典型体M 的n 阶低序体的序号。
图1所示是复合镗铣加工中心结构布局示意图,图2所示为该复合镗铣加工中心铣削部分拓扑结构示意图。在建立拓扑结构时,横梁视为与左立柱、右立柱、床身为一体结构,按床身定义。表1所示为描述该拓扑结构的低序体阵列。

表1 多体系统的低序体阵列
3 特征矩阵
如何建立各部件体之间的特征矩阵是误差建模中重要关键的步骤,两个相邻部件体间的位置与运动关系需要被关联成方程函数的形式,特征矩阵就准确地起到了架接关联两者的作用。在一个多体系统中,相邻部件体间的坐标分为实际位置与运动位置。通常用4 ×4 阶方阵表示,它们分别为静止位置特征变换矩阵、静止位置误差特征变换矩阵、运动特征变换矩阵、运动误差特征变换矩阵。相邻部件体的空间点和空间矢量就是根据这4 种特征矩阵变换完成不同坐标系间的内容表示。
在有误差的多体系统中,任意典型体M 与其相邻低序体Q 之间的静止位置特征变换矩阵为:

静止位置误差特征变换矩阵为:

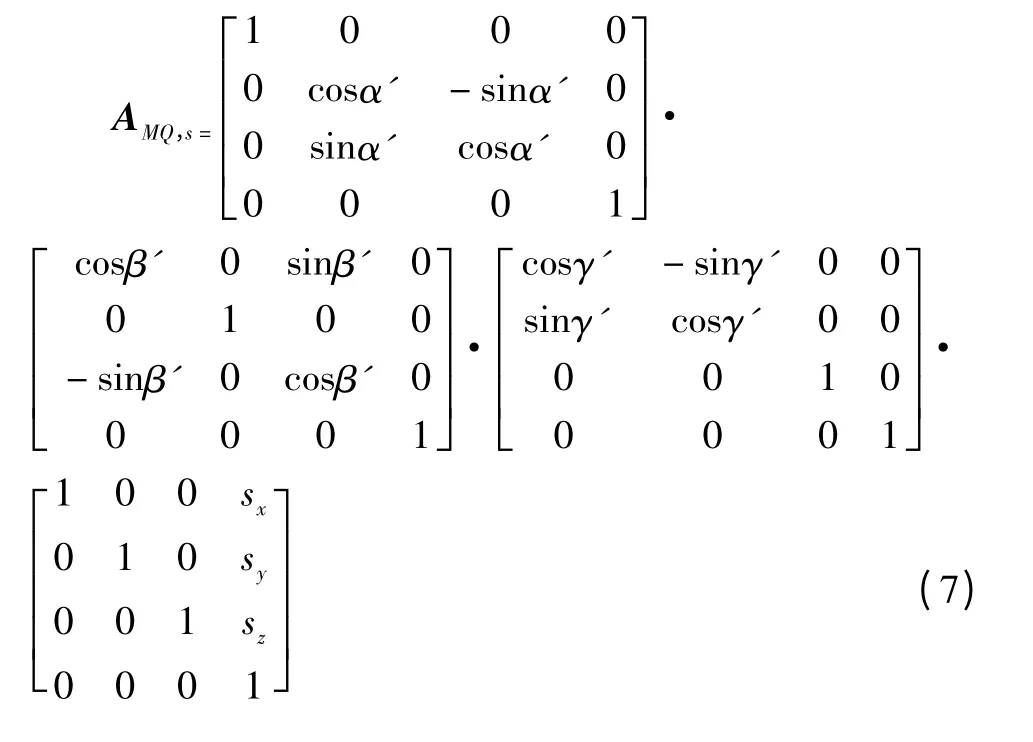
运动特征变换矩阵为:
运动误差特征变换矩阵为:
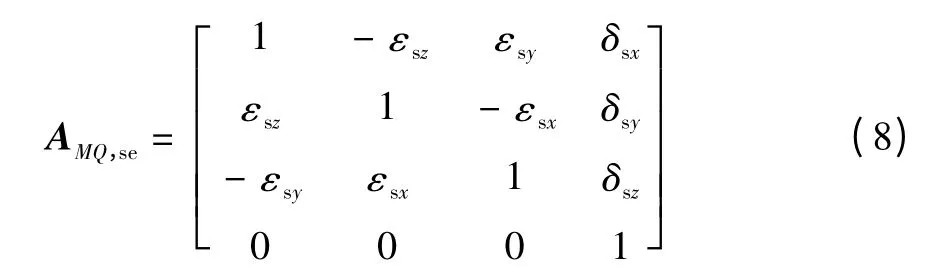
式(5)—(8)中:px、py、pz代表任选典型体M 与其相邻低序体Q 所处的初始静止位置;δpx、δpy、δpz、εpx、εpy、εpz分别是静止位置误差矢量值在X、Y、Z三向坐标轴内的线位移平动量和绕X、Y、Z 三向坐标轴的旋转量;sx、sy、sz是任选典型体M 与其相邻低序体Q 在初始坐标系原点之间相对于X、Y、Z 三向坐标轴的线位移运动平动量;α、β、γ 为静止状态下任选典型体M 相对低序体Q 的3 个方位角;α'、β'、γ'为运动过程后典型体M 变化了的3 个方位角;δsx、δsy、δsz、εsx、εsy、εsz分别是运动误差矢量值在X、Y、Z 三向坐标轴内的线位移平动量和绕X、Y、Z 三向坐标轴的旋转量[4]。
假如任何相邻体M、Q 从最初位置静止状态下开始相对运动,那么在理想状态下其相应的子坐标系间的理想特征矩阵和误差作用下误差特征矩阵分别为:
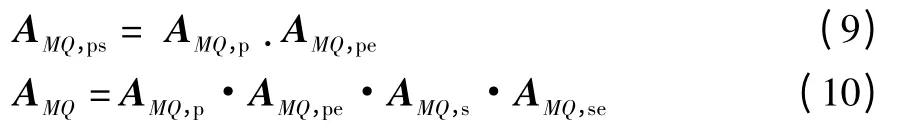
对复合式镗铣加工中心铣削部分的运动部件:X轴滑台支座、绕C 轴分度回转的数控转台、Y2轴滑台、Z2轴主轴箱等进行综合分析,得出了复合镗铣加工中心铣削部分的28 项几何误差,具体误差元素如表2所示。

表2 复合镗铣加工中心铣削部分28 项误差元素
4 建立空间误差数学模型
根据复合式镗铣加工中心铣削部分的结构布局和拓扑结构分析,该铣削部分可分为2 条多体链进行研究。第一条多体链是床身到工件链,包含部件为:床身、X 轴滑台、数控转台、工件。第二条多体链为床身到刀具链,包含部件为:床身(横梁)、Y2轴滑台、Z2轴主轴、刀具。
第一条多体链分析。在第一条多体链上存在4 个部件体,每个部件体含有一个体坐标系(与机床坐标系同向)、一个理想运动参考坐标系、一个实际运动参考坐标系,两个相邻部件体之间的相对位置误差是理想运动参考坐标系与实际运动参考坐标系位置的判定标准。该多体链中,床身静止放置于大地上,假定床身A1体的体坐标系与大地惯性体坐标系重合;X轴滑台A2体中的理想运动参考坐标系重合于床身A1体的体坐标系,又由于X 轴滑台A2体可在安装过程中对导轨以及附属结构精密调整,则相对位置误差不予考虑,所以X 轴滑台A2体的实际运动参考坐标系与理想运动参考坐标系重合;数控转台A3体的理想运动参考坐标系与X 轴滑台A2体的体坐标系重合;工件A4体静止于数控转台A3体上,工件A4体的体坐标系、理想运动参考坐标系、实际运动参考坐标系重合,三者相对于数控转台A3体坐标系平移一个矢量P4= [p4x,p4y,p4z]T。


第二条多体链分析。Y2轴滑台A5体的理想运动参考坐标系相对于床身A1体的体坐标系平移一个矢量P5= [p5x,p5y,p5z]T,实际运动参考坐标系与理想运动参考坐标系转过垂直度误差ε5x和ε5z;Z2轴主轴箱A6体的理想运动参考坐标系与Y2轴滑台A5体的体坐标重合,实际运动参考坐标系相对于理想运动参考坐标系转过垂直度误差ε6x和ε6y;刀具A7体的理想运动参考坐标系与Z2主轴箱A6体的体坐标系重合,实际运动参考坐标系与理想运动参考坐标系相重合[5]。

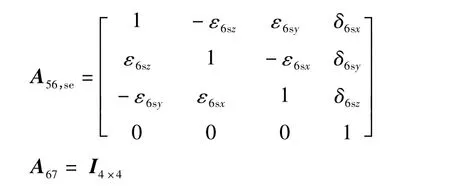
设刀尖在刀具体A7体中的位置矢径t7= [0、0、-k]T,工件A4体坐标系中加工点位置矢径为w4=[Xw、Yw、Zw]T,由于床身坐标系与大地惯性坐标系重合,则刀尖位置矢量和加工点在床身A1体中的位置矢量T1和W1分别为[7]:

5 结束语
基于多体运动学理论创建了精密复合式镗铣加工中心铣削部分的空间误差模型,该误差模型对此加工中心铣削部分的动态优化、精度保障和误差补偿均等后续研究有着重要作用。
【1】邬再新,周伦才,刘涛.用神经网络方法探测机床运动误差通用建模方法[J].组合机床与自动化加工技术,2007(12):23-25.
【2】粟时平,李圣怡.五轴数控机床综合空间误差的多体系统运动学建模[J].组合机床与自动化加工技术,2003(5):15-18.
【3】郭辰,杨林,方庆勇.基于多体系统理论的数控机床误差建模[J].机械设计与制造,2005(3):123-125.
【4】赵小松,方忻,章青.四轴联动加工中心的误差补偿技术的研究[J].中国机械工程,2000,11(6):637-639.
【5】李欢玲.基于多体理论的数控机床几何误差补偿技术的研究[D].南京:南京航空航天大学,2009:13-20.
