一种可实现的仿射组合自适应滤波算法*

郭业才，张冰龙，吴彬彬

(1.南京信息工程大学 江苏省气象探测与信息处理重点实验室,江苏 南京210044;2.南京信息工程大学 电子与信息工程学院,江苏 南京 210044)

在自适应算法的设计中，收敛速度和稳态误差是两个重要的指标，然而在一般的自适应算法设计中，这两个指标往往不能同时达到最佳值，即收敛速度快、稳态误差大，而收敛速度慢、稳态误差小[1]。为了获得收敛速度快、稳态误差小的自适应算法，研究人员提出了自适应滤波算法的凸组合方案[2-5]，它的优点在于组成结构相对简单，并且在稳态和非稳态情况下均有良好的性能[6]。

最近，自适应仿射组合算法被提出[7]，它是凸组合算法的推广。在凸组合算法中，采用sigmoid函数作为组合参数 λ(n)，因此 λ(n)的取值范围是[0,1]；而对于仿射组合算法，组合参数 λ(n)的取值不受区间[0,1]的限制，它的取值在稳态下为负值[8]。组合参数λ(n)是仿射组合算法中重要的控制因子，通过对组合参数的调整，可以实现对每个子滤波器的切换。从理论上说，该仿射组合算法可以获得每个子自适应滤波算法的优点，即同时具有快的收敛速度和小的稳态误差。

本文分析了仿射组合自适应滤波算法的瞬态过程和稳态过程，并提出了一种可实现的更新组合参数的方法。仿真结果表明，该组合参数的性能曲线同时具有快的收敛速度和低的稳态误差，与最佳性能曲线一致。

1 仿射组合自适应滤波算法

仿射组合自适应滤波算法原理框图如图1所示。

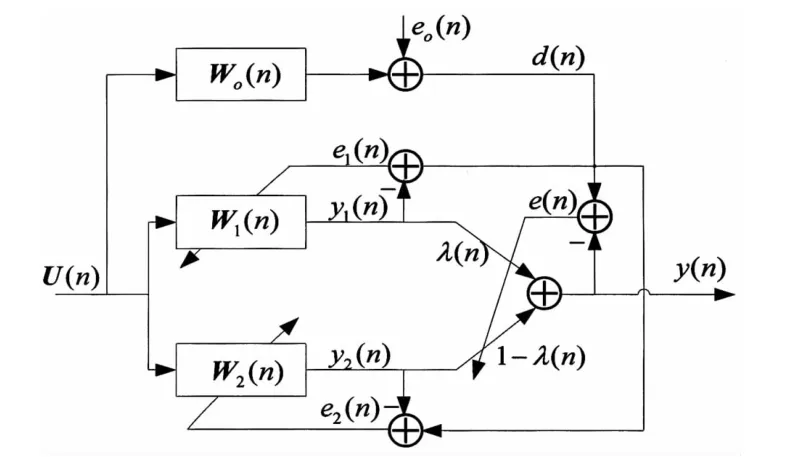
图1 仿射组合自适应滤波算法框图

图1中，每个滤波器均采用 LMS算法，滤波器 1采用的 LMS算法，步长为 μ1；滤波器 2采用的 LMS算法，步长为 μ2；假设 μ2=δμ1,0＜δ＜1。

LMS自适应算法滤波器权向量Wi(n)更新公式为:

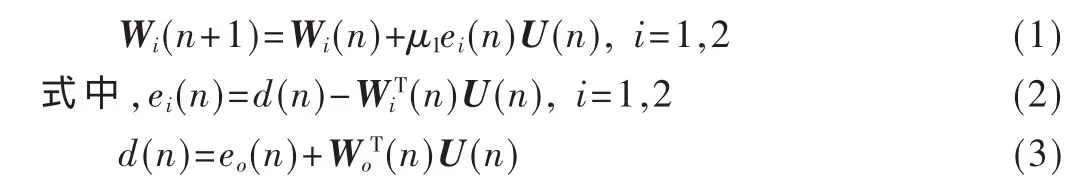
其中，W1(n)是滤波器 1的 N阶权向量，W2(n)是滤波器 2的 N阶权向量。假设 eo(n)是均值为 0、方差为 σo2的噪声信号，并且和其他信号统计独立。U(n)为输入信号，U(n)=[u(n),…,u(n-N+1)]T。

组合后的输出信号为：

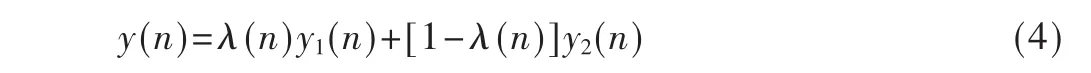
式中，yi(n)=WiT(n)U(n)，i=1,2,λ(n)为组合 参数。 系统误差为:

将 yi(n)代入式(4)中，可得:

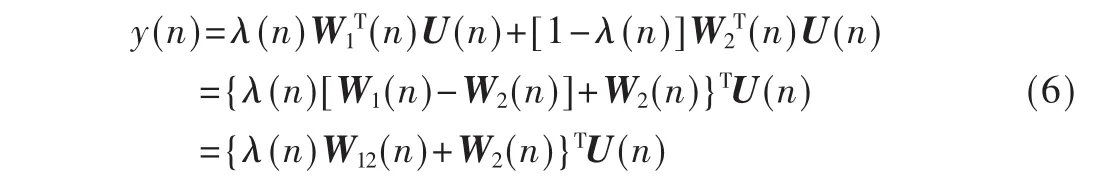
式中，W12(n)=W1(n)-W2(n)

下面求出组合参数λ(n)的最佳表达式λo(n)。由式(3)、(5)、(6)可得:

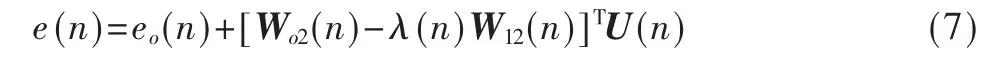
式中，Wo2(n)=Wo(n)-W2(n)

令Ru=E[U(n)UT(n)|W2(n),W12(n)]

由式(7)，对 U(n)取期望，可得:

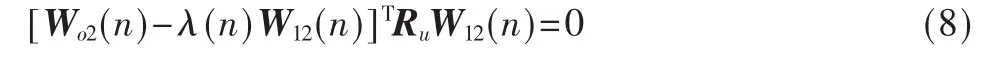
解方程式(8)可得λ(n)的最佳表达式:

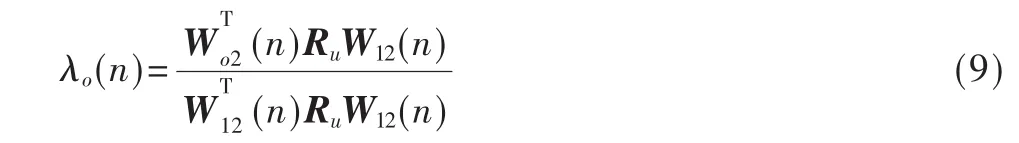
经过适当运算，可得组合参数λ(n)的稳态表达式为:

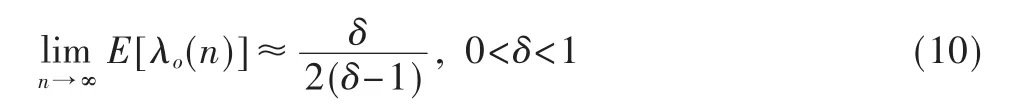
式(10)表明，当系统处于稳态时，λo(n)＜0。

由于两个子滤波器对最佳权向量的估计有一定的相关性，因此在稳态时，λ(n)＜0表明采用子滤波器 1估计系统最优权向量值应当减去用子滤波器2估计系统最优权向量的值，从而避免噪声信号及两个子滤波器对最佳权向量估计的相关性所带来的误差干扰[9]。

2 归一化组合参数λ(n)的更新公式

由于式(9)是在理想情况下得出的，在实际应用中难以实现，因此本文提出一种可实现的归一化组合参数λ(n)的更新公式。

对E[e2(n)|W2(n),W12(n)]求偏导并使它等于0，可得:

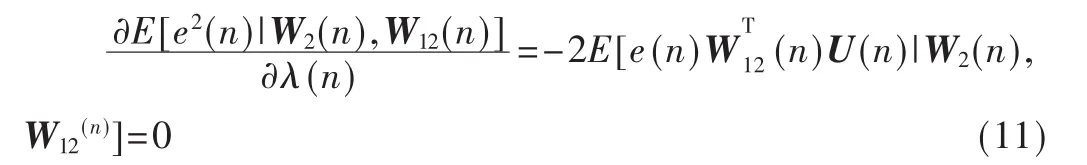
由式(7)及式(11)，可得用随机梯度搜索算法估计最佳组合参数λo(n)的迭代表达式为:

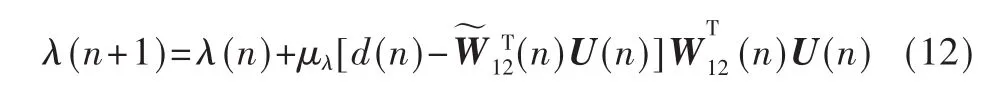
式(12)是组合参数λ(n)的一阶随机时变递归表达式。若 μλ＜1时，式(12)较稳定，但是跟踪子滤波器的性能较差；若 μλ＞1时，系统的跟踪性能较好，但是容易导致式(12)的初始阶段调整的不稳定。因此这里采用类似于NLMS算法形式的功率归一化方案调整参数 μλ，使 μλ在初始阶段小于1，以保持系统的稳定性；在过渡阶段及稳态阶段使μλ大于1，以保证系统对子滤波器具有较好的跟踪性能。令:

式中，φ为参数，ε是很小的正常数，p(n)是信号y1(n)-y2(n)的低通滤波功率估计值，且:

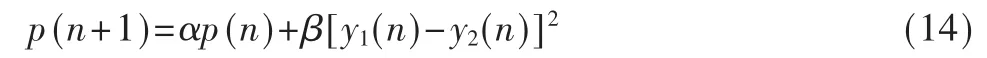
式中，α 和 β为遗忘因子，0＜α,β＜1，通常选取 α 为接近1的值，以便 μλ(n)与组合参数 λ(n)有很小的相关性。 因此式(12)可写为:

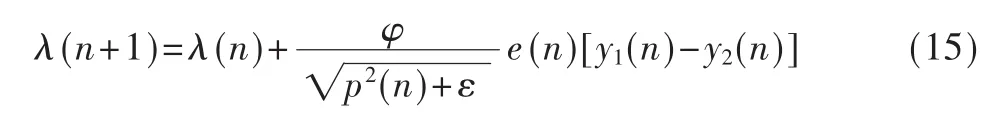
3 仿真分析

假设未知系统为7阶FIR滤波器模型，自适应滤波器的阶次与未知模型阶次相同,并且每次仿真均采用100次蒙特卡洛循环,假设Wo(n)=[0.01，0.03，0.12,0.17,0.11,0.08,0.02],δ=0.2,W1(0)=0,W2(0)=0,α=0.99,β=0.01,φ=3×10-3,ε=0.8×10-3。 系统输入信号为均值为 0，方差为1的高斯白噪声信号。这里采用均方偏差MSD(Mean Square Deviation)表征仿射组合算法的性能。

图2给出了迭代函数μ(n)曲线。图3给出了仿射组合滤波算法组合参数λ(n)曲线。图3中虚线表示由式(9)得出的最佳组合参数λo(n)的曲线，实线表示采用式(15)得到的曲线。图3表明，本文所提出的组合参数λ(n)的曲线和最优组合参数λ(n)的曲线几乎一致，在稳态时，组合参数的值小于零。

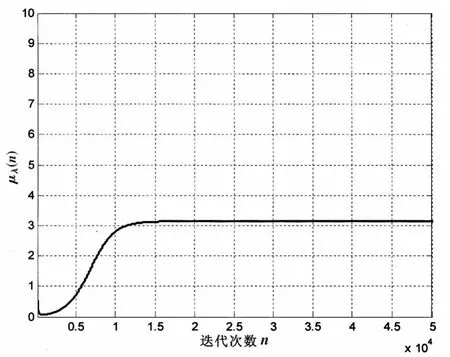
图 2迭代函数μλ曲线

图 3采用式(15)得出的组合参数 λ(n)曲线

图4展示了在理想情况下仿射组合自适应滤波算法的均方偏差性能曲线。图4中收敛较快的曲线是滤波器1的收敛曲线，收敛较慢的曲线是滤波器2的收敛曲线，由于 μ1＞μ2，滤波器 1的收敛速度比滤波器 2的收敛速度快。虚线表示根据理论推导所得出的理想组合算法的均方误差曲线。

图5和图6展示了采用式(15)作为组合参数得出的仿射组合滤波算法稳态偏差性能曲线。两个组成滤波器的步长是固定的，图5中的滤波器1的步长 μ1=0.1，滤波器 2的步长 μ2=0.02。图 6中的 μ1=0.1,μ2=0.03。从图5和图6可以看出，组合后的均方偏差MSDc随着滤波器1和滤波器2的均方偏差变化而变化。在初始阶段，组合滤波器的性能曲线跟随滤波器1的性能曲线；在过渡阶段，组合滤波器的性能曲线逐渐由滤波器1过渡到滤波器2；稳态阶段，组合滤波器的性能曲线跟随滤波器2的性能曲线，改变组成滤波算法的步长值，组合后的算法性能曲线仍然具有良好的跟踪性能。

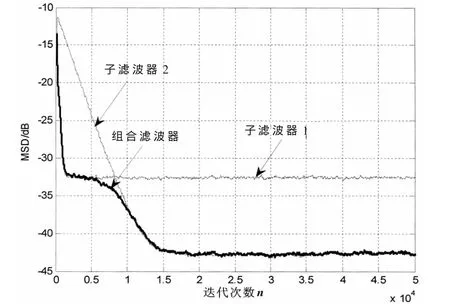
图5 仿射组合自适应滤波算法的MSD性能曲线(a)

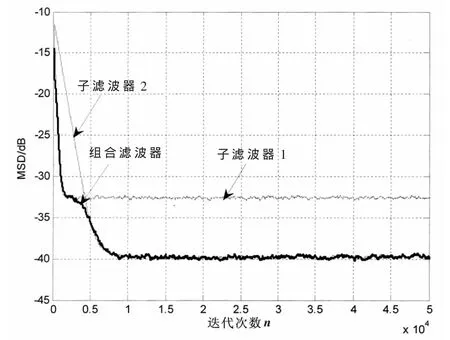
图6 仿射组合自适应滤波算法的MSD性能曲线(b)

仿射组合自适应滤波算法是凸组合算法的推广，仿射组合自适应滤波算法的组合参数λ(n)不受区间[0,1]的限制。在仿射组合算法中，每个子滤波器对未知信道产生独立的估计，因此存在一个最佳仿射组合系数使稳态偏差最小。本文对两个自适应滤波器组成的仿射组合自适应滤波算法的性能进行了分析研究，提出了一个可实现的组合参数λ(n)的更新公式，并得出了相应的仿真结果。仿真结果表明，本文提出的组合参数更新公式与最佳组合参数更新公式一致，采用该组合参数的仿射组合算法可以实现自适应算法快的收敛速度和低的稳态偏差，对信号处理领域研究具有一定的参考价值。

[1]张爱民，王星全.自适应阵列智能天线抗干扰性能研究[J].电子技术应用,2012,38(1):94-96.

[2]于霞，刘建昌，李鸿儒.一种变步长凸组合自适应滤波器及其均方性能分析[J].电子学报，2010,38(2):480-484.

[3]芮国胜，苗俊，张洋,等.基于凸组合的同步长最大均方权值偏差自适应滤波算法[J].通信学报，2012,33(3):28-34.

[4]SILVA M T M,ARENAS G J.A soft-switching blind equalization scheme via convex combination of adaptive filters[J].IEEE Transactions on Signal Processing,2013,61(5):1171-1182.

[5]NASCIMENTO V H,de LAMARE R C.A low-complexity strategyfor speeding up the convergence of convex combinations ofadaptive filters[C].IEEE International Conference on Acoustics,Speech and Signal Processing.Kyoto,2012:3553-3556.

[6]SANG-WOOK S,JEONGKYU L,KYEONG-PYO L,et al.Subband adaptive convex combination of two NLMS based filters for sparse impulse response systems[C].IEEE Statistical Signal Processing Workshop(SSP),Ann Arbor,2012:201-204.

[7]RAJIB L D,BIJIT K D,MRITYUNJOY C.Improve the per Formance of the LMS algorithm via cooperative learning[C].National Conference Communication(NCC),New Delhi,2013:1-5.

[8]KALEEM A M,TAMBOLI A I.An affine combination of two time varying LMS adaptive filters[C].International Conference on Communication,Information&Computing Technology(ICCICT),Mumbai,India,2012:1-4.

[9]BERSHAD N J,BERMUDEZ J C M,TOURNERET J Y.An affine combination of two LMS adaptive filters-Transient mean-square analysis[J].IEEE Transactions on Signal Processing,2008,56(5):1853-1864.