基于磁控电抗器无功规划研究

叶华,赵川,田翠华

(1.云南电力调度控制中心,昆明 65011；2.武汉大学电气工程学院,武汉 430072)

基于磁控电抗器无功规划研究

叶华1,赵川1,田翠华2

(1.云南电力调度控制中心,昆明 65011；2.武汉大学电气工程学院,武汉 430072)

传统的无功规划研究都是基于分组投切电容器这种补偿方式来考虑的,该补偿方式补偿容量不连续,受限制于投切次数,不可实时动作补偿。提出一种基于MCR型SVC的无功规划思想,首先以最小负荷方式下网损最优模型确定单组容量配置和MCR容量下限,然后从经济性出发以净收益最大模型来确定各补偿点总容量配置,两种建模方法相结合最终确定无功配置方案。

磁控电抗器；无功规划

1 前言

随着电力需求不断增加,系统经常运行在重负荷条件下,无功分布不合理导致的电压质量问题和网损较大问题变得越来越严重。电力系统无功规划对保证电压质量、降低电网损耗、实现电网的安全经济运行具有重要的意义。无功规划需具体考虑到无功补偿设备。目前,分组投切电容器组这种补偿方式成本相对较低,但补偿容量不连续,不可实时动作补偿。现有基于相控电抗器(TCR)和磁控电抗器 (Magnetically Controlled Reactor,MCR)的无功补偿装置容量连续可调,但TCR的技性能及经济性均不如MCR[1-6]。

系统的有功损耗最小是无功规划从经济性的角度出发的经典模型。文献 [7]以系统的有功网损最小为目标函数,提出了考虑电源无功优化时电力系统无功最优补偿的数学模型,该模型结果显示能降低网损,提高经济效益。文献 [8]以无功注入总成本最小为目标,文献 [9]以年费用最小为目标函数,将优化问题分解为投资主问题与运行子问题,为无功规划提供了新的思路。文献 [10]采用年电能损失费用与折合为等年值的新增无功补偿设备的投资费用之和最小为目标,用最大负荷损耗时间来协调统一,使得模型更符合实际情况。文献 [11]以全天内电能损耗最小为目标,可以避免对全年负荷预测的不准确性对规划的影响。文献 [12]以补偿后的净收益最大为目标函数,对投资的收益最大化提出了明确直观的模型。以电力市场环境为背景,文献 [12-15]考虑到无功功率的发电和运行成本,采用有功和无功的发电成本最小化作为目标。

目前基于MCR进行无功规划研究的文献极少,本文基于磁控电抗器 (MCR)进行无功规划探索研究,首先以最小负荷方式下网损最优模型确定单组容量配置和MCR容量下限,然后从经济性出发以净收益最大模型来确定各补偿点总容量配置,两种建模方法相结合最终确定无功配置方案。

2 网损最优模型

在最小负荷方式下,单组容量的求解并不涉及总投资,因此采用网损最优模型,目标函数如下：

约束条件包括等式约束条件和不等式约束条件,分别表示如下：

节点有功功率约束：

节点无功功率约束：

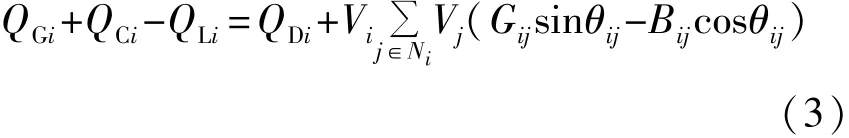
发电机节点电压约束：

VGimin≤VGi≤VGimax,i∈NG(4)

负荷节点电压约束：

VLimin≤VLi≤VLimax,i∈NLD(5)

发电机节点无功约束：

QGimin≤QGi≤QGimax,i∈NG(6)

变压器分接头位置变化范围约束：

KTimax≤KTi≤KTimax,i∈NT(7)

新增无功补偿可装设容量的约束：

QCimin≤QCi≤QCimax,i∈NC(8)

QLimin≤QLi≤QLimax,i∈NL(9)

式中,

PL：系统有功网损；

Vi：节点的电压；

PGI、PGi：节点处发电机的有功功率、无功功率；

QGimax、QGimin：节点处发电机的无功出力上、下限；

PDi、QDi：节 i点处负荷的有功功率、无功功率；

QCimin、QCimax：节i点处待新增电容器最小、最大的补偿容量；

QLimin、QLimax：节i点处待新增磁控电抗器最小、最大的补偿容量；

Gij、Bij和θij：节 i点和 j之间的电导、电纳和相角差；

NB：参与损耗统计的支路；

NT：有载调压变压器支路集；

Ni：与节点i相连的节点集；

NG、NLD：系统中发电机所在节点集、负荷节点集；

NC、NL：待新增无功补偿并联电容器、磁控电抗器节点集。

需要注意的是：该模型中,负荷参数均为最小负荷方式下的参数。其求解结果中,QCi作为待补偿点并联电容单组补偿容量,记为Q△Ci；QLi作为待补偿点 MCR容量,记为 Q△Li,用下式表示为：

QLi=Q△Li,i∈NL(10)

原则上,为实现无功补偿容量连续可调,需要在上述确定的分组投切电容器组节点处 (即处)配置的MCR容量QLi不应小于并联电容单组补偿容量,表示为：

QLi≥Q△Ci,i∈NC(11)

3 净收益最大模型

3.1 网损费用计算

数学模型中的网损费用取决于于系统的网损和电价等因素,其中网损的计算通常折算成最大负荷和最大负荷损耗时间进行计算在最大负荷方式下,子小时的电能损失恰好等于全年的电能损失,则即为最大负荷损耗时间,表示如下：

子=W/PLmax=(PLmax·tmax+PLnor·tnor+PLmin· tmin)/PLmax(12)

全年的电能损失费用可表示为：

FL=KD×PLmax×子 (13)

其中,PLmax、PLnor和PLmin分别为最大、 一般和最小负荷方式下的网损,tmax、tnor和tmin分别为一年中最大、一般和最小负荷方式的运行小时数, KD为系统电价。

3.2 投资费用计算

新增无功补偿设备的投资费用包含两部分费用：补偿装置设备成本投资费用、用于补偿装置维护和运行等的固定年费用。

补偿装置设备成本投资费用表示如下：

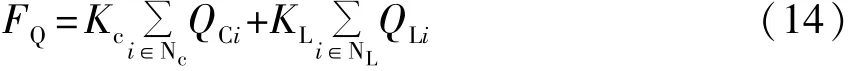
式中,Qci和QLi分别表示对应节点i处电容器和磁控电抗器安装容量,若该点不补偿,则均为零；KC和KL表示对应单位容量的容性、感性无功补偿设备的价格；NC和NL分别表示可新增容性、感性补偿节点集。

补偿装置的经济寿命年限为：m

用于补偿装置维护和运行等的固定年费用：

FQnan=A(15)

考虑到资金的时间价值,这里引入现值、等年值的概念。现值表示将不同时刻的资金折合到当前时刻的等效资金,等年值表示将资金换算为按期等额支付的等效资金。

装设无功补偿装置会在其使用寿命年限产生内一直产生经济效益,可以将前期无功补偿设备的一次性投资FQ转化为经济寿命年限内每年的固定比例投资,即转化为等年值表示。设转化为等年值表示后每年用于设备成本投资费用为x,在补偿装置的经济寿命年限内每年投资x折合到当前时刻的等效资金即为 FQ,设贴现率为 r,则有：

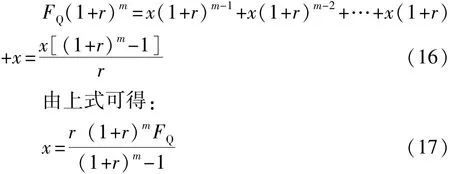
3.3 净收益最大模型的建立

在最大负荷方式下,求得网损费用和无功补偿装置投资费用后,即可得出网损下降带来的经济效益与折合后的投资费用之间的净收益,即无功规划的总收益：

以净收益最大化为目标,则目标函数表示为：

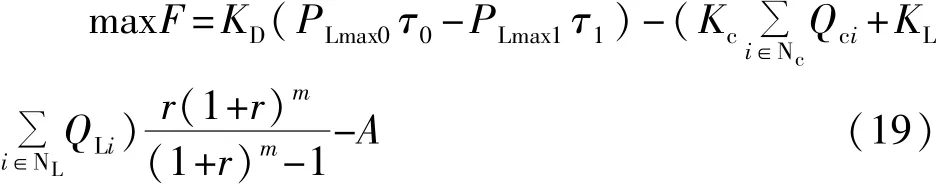
其中,PLmax0和 PLmax1根据补偿前后的最大负荷方式由下式确定：

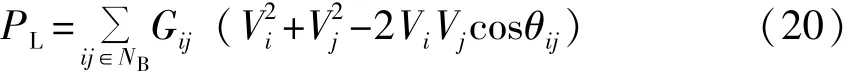
观察目标函数式 (19),其中PLmax0由最大方式下经潮流计算可以确定,在目标函数中是常数,因此KDPLmax0τ0为常数,所以净收益最大化的目标函数也可以等效表示为补偿后的网损费用与折合后不考虑固定费用的投资费用之和最小,即：

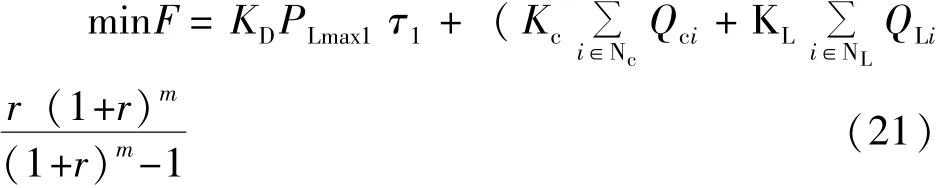
模型的约束条件与网损最优的约束条件有部分差异,在经济性分析时,在节点Nc处配置了并联电容器,相应约束条件应修改为：

Q△Ci≤QCi≤QCimax,i∈Nc(22)还需要考虑在并联电容器组的节点配置了MCR的情况,增加一个约束条件：

Q△ci≤QLi≤QCimax,i∈Nc(23)

对于无功过剩的节点NL,装设了容量连续可调的MCR,容量由式 (10)确定,在净收益最大模型中,不作为总容量变量求解,只作为已有无功补偿装置,则其容量约束表示为：

0≤QLi≤Q△Li,i∈NL(24)

其它约束条件由式 (2) ～ (7)确定。

上述网损最优模型和净收益最大模型的求解是一个典型的连续量和离散量混合的多变量、非线性的优化问题,在本质上可以用同一个优化数学模型来表示,只是目标函数和约束范围有些许差异。目前,用于求解该类优化问题的算法主要分为基于导数的数学规划常规方法和人工智能优化方法两大类求解方法。常规方法包括线性规划、非线性规划、混合整数规划法等几种[16-25]；人工智能方法则主要有遗传算法[26-31]、模拟退火算法[27-28]、人工神经网络法、Tabu搜索方法、差异进化算法[28-29]、 粒子群算法等[32-36]。考虑各方法的优缺点,本文采用改进的预测-校正内点法进行求解。

4 算例分析

选择IEEE 30节点系统进行分析,该系统有6台发电机,节点1作为平衡节点；系统中其他节点为PQ节点；有载调压变压器支路为6-9、6-10、4-12、27-28；可投切电容器组节点有2个。

4.1 选择补偿点

通过选择无功补偿主导节点提供三种无功补偿节点选择方案,即：

方案一：12、19、26、30四个节点；

方案二：12、17、19、21、30五个节点；

方案三：12、17、19、21、26、30六个节点。

4.2 电容器单组容量和MCR容量下限

取IEEE 30节点系统负荷水平的0.5倍为最小负荷方式,分别计算基于三种无功补偿点选择方案的网损和未进行无功规划补偿的网损,参见表1。

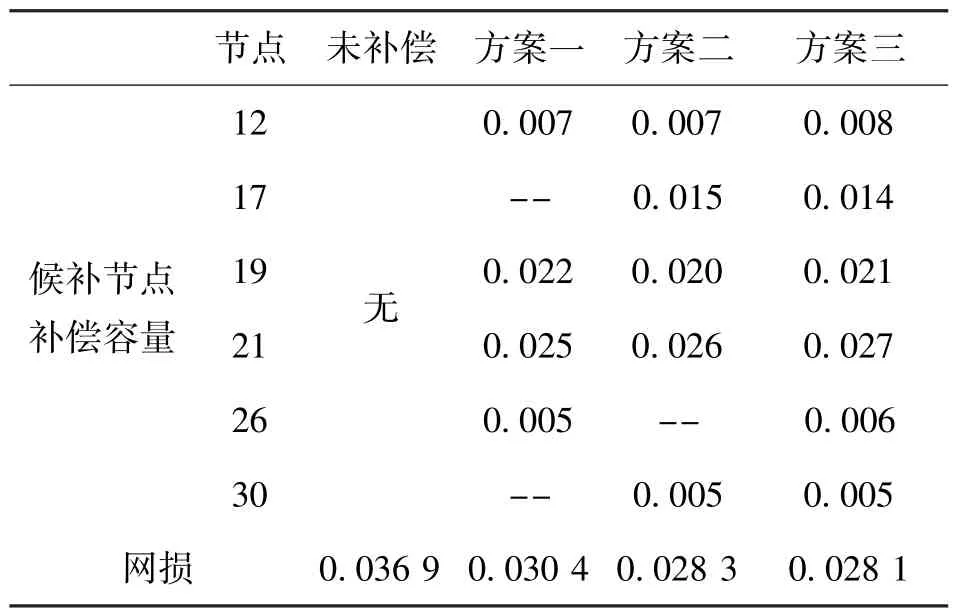
表1 各方案最小负荷方式下的优化结果 (p.u.)

从表1可知,比较方案一、方案二和方案三,补偿节点越多,系统网损也越小。随着补偿节点增多,网损虽有所下降,但幅度越来越小,因此,从经济性方面考虑时,并非补偿点选得越多越好。

表1给出了在最小负荷方式下候补无功补偿点相应的容量,即容性无功功率的容量,若采用电容器组分组投切方式进行无功补偿时,可以参考该容量作为单组容量。本文基于磁控电抗器无功规划,目的就是在进行无功补偿时能够提供从0开始连续可调的无功功率补偿,因此,配置相应的MCR容量一般以不低于单组无功补偿电容器组容量为原则,本文MCR容量配置的下限参照单组电容器组容量来确定,见表2。

表2 MCR容量配置下限

4.3 电容器组数和MCR容量

要确定电容器组数和MCR容量,即总的容量配置,通过求解净收益最大模型来实现。系统基准功率为100 MVA,最大负荷方式取IEEE 30节点系统负荷水平的1.5倍,最大负荷方式、一般负荷方式、最小负荷方式运行小时数分别为2 000小时、4 760小时、2 000小时。系统电价为0.55元/kWh,电容器价格为8万元/Mvar,MCR价格为10万元/Mvar,所有设备的使用年限为20年,贴现率取2.5%。

首先计算三种负荷方式下的损耗和最大负荷损耗时间,计算结果见表3。

表3 各方式下的损耗和最大负荷损耗时间

以年总费用为目标,考虑变压器变比的离散性,运用改进预测-校正内点法,求解方案一、方案二和方案三对应的候补节点容量配置。其中MCR容量配置均取表5-4所示的容量下限,这也是比价符合实际的。因为在最小负荷方式下,由于优化了发电机节点电压,没有其他节点因为无功过剩、节点电压过高,因此不需要配置感性无功。所以MCR的配置在该系统中只是为了与投切电容器组合形成容量连续可调的无功补偿装置。其容量配置超过下限并不能增大容性无功补偿上限,反而会降低经济性,因此从经济性方面优化后,MCR容量配置定为表2所述的容量下限。

为了对比分析基于磁控电抗器的无功规划的经济性,在最大负荷方式下,优化计算得到总费用最低的投切电容器规划方案,分别将其与方案一、方案二和方案三所对应的MCR型SVC优化结果进行比较。所选三种补偿方案均产生较大的经济效益。其中方案二和方案三分别补偿了五个和六个节点,其中21号节点补偿容量较大,降损作用优于方案一,因此其年收益要高于方案一。方案三较方案二增加了在节点26补偿0.006×2Mvar的容量,在该节点补偿后网损较方案二略有下降,从系统结构图可以看出,与节点26相连的节点25无负荷,但是其附近的节点24和节点30均装有无功补偿装置,因此节点26本身可以通过节点24和节点30的无功补偿装置进行一定的无功补偿,所以增加节点26进行无功补偿网损降低不显著,但是等值年固定投资费用却高于方案二,导致年收益非常接近。

5 结束语

对于每一种补偿点选择方案,使用MCR型SVC进行补偿所产生的年收益均大于同方案使用投切电容器组来补偿。基于磁控电抗器的无功规划可以作为选择无功补偿方式在经济性方面的一个参考,使用MCR型SVC进行无功补偿的经济效益高于投切电容器组补偿方式。

[1]陈柏超,陈维贤.特高压可控电抗器及其大幅度限压问题[J].高电压技术,1995(2)：11-14.

[2]田翠华,陈柏超.磁控电抗器在750 kV系统中的应用 [J].电工技术学报,2005(1)：31-37.

[3]田翠华,陈柏超.可控电抗器在西北750 kV系统中的应用[J].高电压技术,2005(3).

[4]陈柏超,田翠华.电磁式特高压统一潮流控制器 [J].高电压技术,2006(12)：96-98.

[5]余梦泽,陈柏超,曹志煌,等.110 kV并联可控电抗器及其应用 [J].电力系统自动化,2008(3)：87-91.

[6]陈柏超.新型可控饱和电抗器理论及应用 (第1版)[M].武汉：武汉水利电力大学出版社,1999.

[7]杨毅刚,吴振球,周竑.考虑电源无功优化时电力系统的无功最优补偿 [J].中国电机工程学报,1991(S1).

[8]Granville S.Optimal reactive dispatch through interior point methods[J].IEEE Transactions on Power Systems.1994,9(1)：136-146.

[9]付瑾诚,肖国泉,舒隽.基于线性规划的 Benders分解法在无功规划中的应用 [J].电网技术,1998(11)：32-35.

[10]李林川,王建勇,陈礼义,等.电力系统无功补偿优化规划[J].中国电机工程学报.1999(2).

[11]摄伟,刘健,周艳.考虑时段优化的地区电网无功电压优化控制 [J].电力系统自动化,2009(4)：31-35.

[12]赵俊光,王主丁,张宗益,等.基于节点补偿容量动态上限的配电网无功规划优化混合算法 [J].电力系统自动化, 2009(23)：69-74.

[13]戴彦,倪以信,文福拴,等.电力市场下的无功电价研究[J].电力系统自动化,2000(5)：9-14.

[14]黄志刚,李林川,杨理,等.电力市场环境下的无功优化模型及其求解方法 [J].中国电机工程学报,2003(12)：82-86.

[15]于辉,赵冬梅.单边开放电力市场下的无功电价研究 [J] .电网技术,2004(14)：62-67.

[16]Momoh J A,El-Hawary M E,Adapa R.Review of selected optimal power flow literature to 1993.Part I：Nonlinear and quadratic programming approaches[J].IEEE Transactions on Power Systems,1999,14(1)：96-104.

[17]Sun D I,Ashley B,Brewer B,et al.OPTIMAL POWER FLOW BY NEWTON APPROACH.[J].IEEE transactions on power apparatus and systems,1984,PAS-103(10)：2864-2880.

[18]寸巧萍.电力系统无功优化算法综述 [J].电气开关, 2007(5)：16-20.

[19]罗铸.电力系统无功和电压的优化调节 [J].电力系统自动化,1988(1)：9-15.

[20]沈如刚.电力系统无功功率综合优化——二次规划法 [J] .中国电机工程学报,1986(5)：42-50.

[21]姚奕荣,张连生,田蔚文.混合整数规划的精确罚函数 (英文)[J].运筹学学报,2002(4)：1-7.

[22]孟志青,胡奇英,杨晓琪.一种求解整数规划与混合整数规划非线性罚函数方法 [J].控制与决策,2002(3)：310 -314.

[23]倪明放,徐南荣.混合整数线性规划的初始可行解 [J].东南大学学报,1992(6)：121-126.

[24]李乃湖.计及整型控制变量的电压一无功功率优化 [J].电力系统自动化,1994(12).

[25]范宏,韦化.基于扰动KKT条件的原始-对偶内点法和分支定界法的最优潮流研究 [J].电力自动化设备,2004(5)：5-9.

[26]向铁元,周青山,李富鹏,等.小生境遗传算法在无功优化中的应用研究 [J].中国电机工程学报,2005(17)：48 -51.

[27]范征.混合智能优化算法在电力系统无功优化中的应用研究 [D].山东大学,2008.

[28]陈奇.电压无功优化算法的比较研究 [D].浙江大学,2008.

[29]Kazemi A,Shayanfar H A,Aghaei J,et al.A new method for optimal reactive power pricing considering power losses and voltage profile[J].WSEAS Transactions on Circuits and Systems, 2005,4(9)：1166-1171.

[30]Li F,Pilgrim J D,Dabeedin C,et al.Genetic algorithms for optimal reactive power compensation on the national grid system [J].IEEE Transactions on Power Systems,2005,20(1)：493-500.

[31]Subbaraj P,Rajnarayanan P N.Optimal reactive power dispatch using self-adaptive real coded genetic algorithm[J].Electric Power Systems Research,2009,79(2)：374-381.

[32]陈蕊,夏安邦,马玉龙.电力系统无功优化算法综述 [J].东北电力技术,2006(6)：38-41.

[33]曹立霞.大型互联电力系统分布式并行无功优化的研究[D].山东大学,2005.

[34]张庭场,耿光飞.基于改进粒子群算法的中压配电网无功优化 [J].电网技术,2012,02：158-162.

[35]赵冬梅,邱辰,张旭.地区电网可视化实用无功优化与规划系统的设计 [J].电力系统保护与控制,2013,03：123-127.

[36]汪超.基于云混沌粒子群算法的配电网无功规划优化[D].上海交通大学,2011.

The Exploratory Research of Reactive Power Planning Based on Magnetically Controlled Reactor

YE Hua1,ZHAO Chuan1,TIAN Cuihua2

(1.Yunnan Power Dispatching Control Center,Kunming,650011；2.School of Electrical Engineering Wuhan University,Wuhan,430072)

Traditional reactive power planning studies are based on switched capacitors.Compensation capacity of the compensation is not continuous and can’t make real-time motion compensation subjecting to limited switching frequency.This paper proposes a reactive power planning ideas based on MCR-type SVC.First,this paper create minimum-loss model under minimum load mode.It can calculate the optimal capacity of single unit capacitor and capacity limit of MCR.Then this paper create maximum net income model economically.It can get the total capacity allocation of reactive power compensation.So we can get optimal Reactive Power Planning program by combining both methods finally.

magnetically controlled reactor；reactive power planning

TM73

B

1006-7345(2014)02-0007-05

2013-11-11

叶华 (1987),男,工程师,主要从事电网调度自动化系统高级应用功能开发工作 (e-mail)yehua_whu@qq.com。