基于聚类蚁群算法的动态无功优化

周鑫，许守东，段晓，顾瑛

(1.云南电网公司电力研究院，昆明 650217；2.国网南阳供电公司，河南 南阳 473000)

基于聚类蚁群算法的动态无功优化

周鑫1，许守东1，段晓2，顾瑛2

(1.云南电网公司电力研究院，昆明 650217；2.国网南阳供电公司，河南 南阳 473000)

针对动态无功优化中需要限制电容器开关和有载分接开关 (OLTC)分接头等离散控制设备动作次数要求，首先，提出离散控制设备无需动作时间概念，该方法统一考虑全天系统负荷变动情况，在保证离散控制设备动作效率基础上使全天动作次数满足要求。另外，将聚类方法与蚁群算法相融合提出聚类蚁群算法，该方法能够根据系统的变化，随时调整路径上的信息素更新浓度。最后，根据引出的路径多样性，可以防止因信息素的过度积累使算法早熟、减少算法搜索次数的优点，提出多时段间路径多样性的概念，以达到降低控制设备的动作次数。对IEEE 14节点和IEEE 30节点系统进行计算，结果验证了方法的可行性、正确性和有效性。

动态无功优化；无需动作时间；聚类蚁群算法；路径多样性

0 前言

电力系统动态无功优化是一个大规模非线性多时段的混合整数规划问题。实际中负荷随时间变化，这就要求控制设备应实时调节以满足系统运行的需要；而考虑控制设备动作次数的限制则进一步加强了它们之间在空间上和时间上的关联，使问题更复杂。所以如何有效地安排控制设备的调节是电力系统动态无功优化的重要问题之一。

相关研究人员针对如何控制离散控制设备动作次数问题进行许多研究。文献 [1]根据负荷曲线变化的剧烈程度将其分为满足约束条件的负荷段，从而把问题转化为静态优化问题，但其要求所有控制设备在相同时间动作。文献 [2-3]通过设定各目标权重的方法，分别将全天电容器组投切次数和OLTC分接头动作次数最少引入到目标函数中。这样，把问题转化为在保证控制设备动作次数最少和满足相关约束的条件下，使系统满足有功网损最小等目标要求的动态无功优化问题。文献 [4]提出动态无功优化调度中控制设备调节代价的数学模型，将控制设备的使用寿命转化为开关动作次数，并根据设备的投资费用与总动作次数之间的关系来确定每次开关调节代价。文献 [5-6]提出采用离散惩罚机制的非线性原对偶内点法求解动态无功优化问题。该方法能够较好地解决变量离散化和控制设备动作次数限制之间的配合问题。文献 [7]在开关日动作次数约束的基础上，同时将分接头档位的相邻时段动作次数作为约束条件，使模型更具实际意义。

动态无功优化问题是一个大规模非线性混合整数规划问题，本文提出离散控制设备无需动作时间概念，限制离散控制设备全天动作次数。同时将层次聚类法和蚁群算法相融合提出聚类蚁群算法和引入路径多样性概念，保证算法能够根据系统变化，调整信息素的更新浓度，以得到更佳的优化结果。

1 动态无功优化的数学模型

本文采用文献 [7]动态无功优化模型。

式中：XCt为t时段的连续控制变量，包括发电机电压幅值VGt；XDt为t时段的离散控制变量，包括并联电容器组的无功补偿容量QCt和OLTC分接头变比TAPt；XSt为t时段的状态变量，包括负荷节点的电压 VDt和发电机的无功注入量 QGt；Cm，t为第m个电容器开关t时段的状态，1为闭合，0为断开；⊕ 为异或运算符；Tl，t为第 l个OLTC的分接头t时段的档位值；Mm为第m个电容器开关的日允许动作最大动作次数；Kl为第l个OLTC分接头的日允许最大动作次数。kl为OLTC分接头的相邻时段最大动作次数。文中认为分接头每调节一档或电容器每投 (切)一次即动作一次。

2 离散控制设备无需动作时间

电力系统动态无功优化主要是根据各时段负荷水平调节控制设备的状态，使系统的全天电能损耗达到最小。但考虑到电容器开关和OLTC分接头等离散控制变量的使用寿命，必需对它们的全天动作次数进行限制。由于不同时段间控制设备的调节效率，与该时段负荷变化率幅度相关。所以在优化前通过分析全天负荷率曲线的变化，本文提出离散控制设备无需动作时间概念。在优化过程中，若某离散控制设备在无需动作时间段内调节过，则之后优化时系统有功网损在未达到某设定精度前不再对该设备进行调节，以达到减少该控制设备的动作次数的目的。

式中：FT-t为T-t时段的负荷率差值；Ta表示T时段对应的无需动作时间；A为对变压器和电容器分别通过仿真实验使其动作次数能够尽量接近全天动作次数限制得到的常数。

3 动态无功优化聚类蚁群算法

蚁群算法是一种随机搜索优化算法，已在电力系统中得到运用[8]，本文借用该算法求解动态无功优化问题。

3.1 初始信息素的形成

文中在形成各时段信息素前，均对每个控制设备进行一次试调节，加强控制作用明显的控制设备所对应路径上的信息素浓度，同时在优化时保证全部蚂蚁第一次均选择到最有效的控制设备。

式中：Pi为T时段第一次调节控制设备i得到的有功网损；N为控制设备个数；τ'iT(0)为控制设备i对应路径上的初始信息素。

3.2 聚类方法与蚁群算法的融合

为保证蚁群的信息素更新能反映系统变化，本文将层次聚类法与蚁群算法相融合。控制设备每次调节后，通过聚类方法分析寻找该时段新的补偿点位置，并与系统补偿点进行对比分析，以确定各路径信息素的更新浓度，具体方法如下：、

3.2.1 蚂蚁选择电容器为动作设备

通过聚类分析选出新的补偿点，若电容器对应的补偿点属于新补偿点集合，则修正有功网损变为原来E倍，反之不变化，如式 (11)所示。

式中：ΔPkim为蚂蚁m第k次调节控制设备i后的系统有功网损；ΔP'kim为蚂蚁m第k次控制设备i调节后的修正有功网损；Dc为补偿点的位置；E为小于1的常数。

3.2.2 蚂蚁选择OLTC或可控发电机为调节设备

通过聚类分析该条件下得到m个新补偿点，并判断m个补偿点中与初始补偿点位置不一致点的数目。位置不一致补偿点的个数越多，说明初始补偿点为新补偿点的个数越少。因此，蚂蚁对应的有功网损变化量越少，如式 (12)所示。

式中：n1为安装电容器节点的个数；n2为聚类分析得到的与初始补偿点位置不一致补偿点的个数。由式 (12)可见，若全部补偿点位置一致，则n2为0，此时ΔP'(k)im为原来对应有功网损的E倍，反n2等于n1，ΔP'kim为原来对应有功网损。

3.2.3 聚类蚁群算法信息素更新规则

式中：τiT(k)、Δτ'iT(k)分别为在T时段第k次搜索 (后)控制变量i的信息素和变化量；τiT(k+1)为蚂蚁第k次搜索后控制变量i的信息素；SC为控制设备集合；ΔP'k'i为在对控制设备i调节后有功网损的平均值；Mi为对控制设备i进行调节的蚂蚁数。

式 (14)表示每次搜索后信息素的修正量，从该式可看出，某控制设备对应路径上信息素浓度的修正量，与该控制设备调节后的有功网损成反比的关系，调节后系统有功网损越小，则其对应的路径上的信息素浓度越强。

3.2.4 蚁群算法连续控制变量搜索策略

文中对离散控制变量采用与文献 [9]相同的搜索策略和状态转移概率规则。同时选定补偿节点的灵敏度、流过OLTC末端的无功电流和发电机无功不平衡量分别作为电容器、OLTC和发电机的启发式因子，启发式因子均取负值。

动态无功优化模型中，没有考虑对连续控制变量发电机的调节次数进行限制，但对发电机机端电压的调整，将对系统全天电能损耗造成明显的影响。所以本文设定蚁群在进行选择时将优先选择到发动机，直到对其调节后系统有功损耗不再下降，则将对应的发电机放入禁忌表中，该时段内则不再对其搜索。

4 蚁群算法多样性

4.1 路径多样性对信息素的影响

蚂蚁在寻优过程中，主要是依靠 “正反馈”原理寻找最优解。在优化初期使蚁群能够快速向最优解靠近。但单纯依靠该原理进行动态无功优化寻优将会产生2点不足。

1)根据蚁群算法的 “正反馈”原理，某些控制设备对应路径上的信息素将会被不断强化，导致蚁群选择这些路径的概率不断加强，最终蚂蚁只对少数控制设备的路径进行搜索，使算法陷入早熟状态。

2)由于蚁群算法本质上均属于随机搜索方法，若某控制设备调整效果较差，但其路径上信息素浓度较高，蚁群反复对其调整，增加蚁群的搜索次数。

因此本文借用遗传算法中种群多样性思想[10]，提出蚁群算法的路径多样性概念，对式(14)聚类蚁群算法信息素修正量进行改进。

式中：Zih为控制变量i在第h次调节的动作次数；k为蚂蚁搜索次数；fi表示控制变量i的多样性系数；ΔτiTk()分别为在T时段第k次搜索(后)控制变量i的信息素变化量；C为常数；B为常数。

从式 (17)第二项可看出路径多样性系数对信息素的影响程度，随着搜索次数增加而不断加强。这样既保证算法在搜索初期快速向全局最优解靠拢，而在搜索后期保持算法选择不同路径的能力，改善算法的局部搜索能力，抑制算法早熟现象，并减少蚁群算法的搜索次数。

4.2 多时段路径多样性对信息素的影响

在电力系统动态无功优化中，若蚁群在不同时段反复选择相同控制设备调节，可能使该控制设备动作次数超出全天动作次数限制，借鉴路径多样性的思想，本文提出多时段路径多样性的概念。如果某控制设备在之前时段动作次数较多，则减少对应路径上的初始信息素浓度，反之增加，如式 (18)：

式中：T为当前时段；Dit为控制设备i在t时段的动作次数，N为控制设备个数。τiT(0)为改进后的初始信息素。

文中提出的动态无功优化聚类蚁群算法流程如图1所示。

图1 算法流程图

1)进行初始潮流计算，确定初始待补偿点；

2)根据负荷曲线，确定无需动作时间值；

3)判断是否24个时段全部计算完；如果计算完输出结果；如果没有转到4)；

4)确定无需动作的设备；

5)根据信息素计算蚂蚁的转移概率，并选择下一状态；

6)进行无功调节，并根据潮流结果进行聚类；

7)判断是否满足约束条件；如果满足转到3)；否则转到5)；

5 算例分析

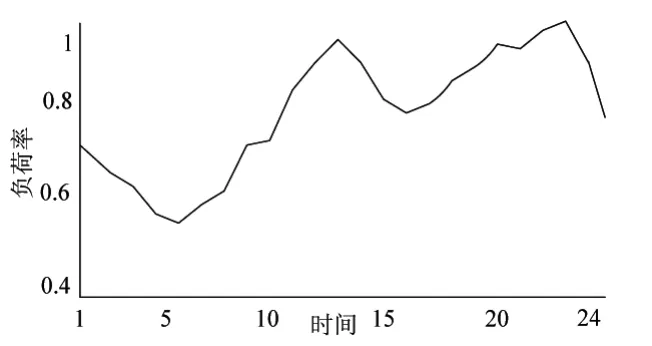
图2 系统负荷率曲线

文中在MATLAB环境下编制程序。对IEEE 14、30节点系统计算时，其补偿点、补偿容量、可控发电机均与文献 [7，11]一致；优化参数设置如下：OLTC分接头全天最大允许动作次数和单个时段允许动作次数分别为Kl=10、kl=3；单组电容器全天最大次数Mm=4；蚁群算法参数取为：ρ=0.5，B=100，a=1，b=10，E=0.5。负荷率曲线如图2所示。

5.1 算法有效性分析和参数选取

5.1.1 路径多样性对信息素的影响

1)参数E的选取

图3给出在考虑多时段信息素和系统多样性影响条件下，参数E从0.3～1调整，系统电能损耗的变化曲线。从图3可看出，系统全天电能损耗值随参数E的调整呈V字形曲线变化。参数E从0.3～0.5变化时，系统的全天电能损耗不断减小；由0.5～1调整时，电能损耗则不断增加。

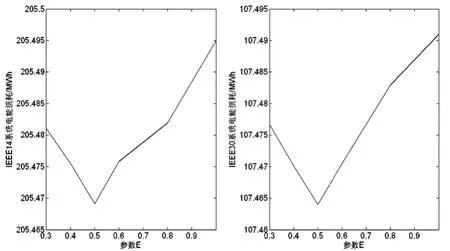
图3 调节参数E电能损耗优化曲线

通过分析，当E＞0.5时，使有功网损的修正幅度减小，减弱聚类算法对蚁群寻优的影响能力；反之，当E＜0.5时，则增加有功网损的修正幅度，从而增大聚类算法对蚁群寻优的影响。当E =0.5时，能够在现有条件下，最大程度发挥聚类蚁群算法的寻优能力。因此，通过将仿真参数E选定为0.5。

2)聚类蚁群算法有效性

表1中方法一、方法二分别表示对常规蚁群算法、不考虑多样性影响的聚类蚁群算法优化计算.

表1 聚类蚁群算法有效性分析

从表1可看出，蚁群算法和聚类蚁群算法的电能损耗分别为206.885 6 MW·h、205.967 5 MW·h，聚类蚁群算法与蚁群算法相比的优化后电能损耗下降0.918 1 MW·h。由于聚类蚁群算法在每次调节之后均对各控制设备的有效性进行分析，再对各路径上信息素浓度进行更新，使蚁群搜索更加有针对性，有效地减低了系统的全天电能损耗。

5.1.2 蚁群算法路径多样性参数选取

1)参数C的选取

文中在考虑聚类影响的条件下，绘制参数C从0～2调整时系统全天电能损耗的变化曲线。

从图4中可以看出，C从0～1.2变化时，系统的电能损耗逐渐减少；从1.2～2变化时，则系统电能损耗增大；当C=1.2时，系统全天电能损耗值最小。通过分析，当C值较大时，蚁群受路径多样性系数影响较大，减弱蚁群搜索到控制设备所对应路径上的信息素浓度，无法使算法收敛于最优解；当C较小时，蚁群搜索后期受到路径多样性系数影响较小，蚁群容易搜索到相同的路径，使蚂蚁搜索后期陷入局部最优解。因此，本文将C选定为1.2。

图4 调节参数C电能损耗优化曲线

2)路径的多样性参数的分析

方法一、方法二分别为考虑或不考虑路径多样性系数影响的两种条件下优化，计算结果如下：

表2 路径多样性有效性分析

从表2可看出，考虑路径多样性系数影响时，对IEEE14、30两个标准系统优化时搜索次数分别为19、24次，而未考虑该影响时搜索次数分别为27、31次，说明对信息素更新时，如果考虑路径多样性的影响能够减少算法的搜索次数。

3)多时段路径多样性有效性分析

方法一、方法二分别表示在考虑和未考虑多时段路径多样性系数条件下，对两个标准系统20次优化后结果。其中参数C=1.2、E=0.5。

表3 多时段路径多样性有效性分析

表3列出20次优化中电能损耗最接近平均值的结果，由该表可看出，若考虑和不考虑多时段路径多样性时，IEEE14节点系统电容器的投切次数分别为42、51次，OLTC动作次数分别为24、27次。考虑多时段间路径多样性系数时，离散控制变量的动作次数较小。IEEE30结果与IEEE14系统相似。

从图5可看出，考虑多时段控制设备动作的影响时，IEEE14节点系统20次优化时电容器动作次数比未考虑该影响时要少5次以上，而OLTC分接头在第4、12两次优化时不小于未考虑该影响时的值。进一步说明考虑多时段路径多样性对能够减少离散控制设备动作次数的有效性。

图5 20次优化离散控制设备动作次数

通过以上3个方面对蚁群算法信息素更新规则的修改，分别起到降低系统电能损耗、减少蚂蚁的搜索次数和离散控制设备的动作次数的目的，表明对信息素更新规则修改的正确性。

5.2 优化结果分析

文中对IEEE14系统，分别在四种情况下优化计算。情况一、二为在聚类蚁群算法条件下分别计算考虑无需动作时间条件和不考虑该条件的优化结果；情况三、四为在非聚类蚁群算法条件下考虑无需动作时间条件和不考虑该条件的优化结果。

表4、5分别列出对情况1～情况4进行20次优化后电能损耗和最优解对应的离散控制设备动作次数。情况5、6分别为文献 [7、11]优化结果。

从表4可以看出，情况1、2全天电能损耗最优解分别为205.468 7、205.462 8MWh，比情况3、4的电能损耗205.475 7、205.473 4 MWh分别要小0.007 0、0.010 6 MWh，小于表1中只考虑聚类蚁群算法时相差0.918 1 MWh，聚类蚁群算法在考虑多样性影响的条件下，系统全天电能损耗变化相对并不明显，但聚类蚁群算法仍能够进一步增强算法的寻优能力。另外从表中可以看出，情况1、2全天电能损耗最优解优化结果小于情况5、6条件下的电能损耗 205.47、209.52 MW h，说明将聚类方法与蚁群算法相融合的有效性。

表4 IEEE14系统电能损耗优化结果

表5 IEEE14系统离散控制设备动作次数

从表5可看出，情况1、3在优化过程中考虑全天无需动作时间条件，它们OLTC分接头的全天最大动作次数分别为8、10次，满足OLTC全天动作次数不超过10次的限制条件[12]；而情况2、4没有计及该条件，它们OLTC分接头的全天最大动作次数则分别为13、12次。说明考虑全天无需动作时间条件，能够更有效地分配控制设备的动作次数。在情况6条件下，由于其限制离散控制设备最大动作次数为2次，因此其离散控制设备动作次数最少，但电能损耗相对较大。

6 结束语

1)根据系统负荷率变化，提出无需动作时段约束条件，使电容器和OLTC分接头等离散控制变量满足全天动作次数的要求，以保证它们的使用寿命。

2)提出聚类蚁群算法。蚂蚁每次对某控制变量调节后，运用层次聚类法分析系统当前状态。通过融合使信息素的更新方向与系统状态变化一致，保证了蚁群算法的全局寻优能力。

3)引出路径多样性概念，使算法跳出局部最优解的能力增强，减少蚁群搜索次数。提出多时段路径多样性，以减少控制设备全天动作次数。

[1] 邓佑满，张伯明，田田.虚拟负荷法及其在配电网络动态优化中的应用 [J].中国电机工程学报，1996，16(7)：241-244.

[2] Lu Feng-Chang，Hsu Yuan-Yih.Fuzzy Dynamic Programming Approach to Reactive Power/voltage control in a distribution substation[J].IEEE Trans on Power Systems，1997，12 (2)：681-688.

[3] Liang Ruey-Hsun，Wang Yung-Shuen.Fuzzy-Based Reactive Power and Voltage Control in a Distribution System[J]. IEEE Trans on Power delivery，2003，18(2)：610-618.

[4] Zhang Yong-jun，Zhen Ren.Optimal Reactive Power Dispatch Considering Costs of Adjusting the Control Devices[J].IEEE Trans on Power Systems，2005，20(3)：1349-1356.

[5] M.B.Liu，Claudio A.Canizares，W.Huang.Reactive Power and Voltage Control in Distribution Systems with Limited Switching operations[J].IEEE Trans on Power Systems，2009，24(2)：889-899.

[6] 刘明波，朱春明，钱康龄，等.计及控制设备动作次数约束的动态无功优化算法 [J].中国电机工程学报，2004，24 (3)：34-40.

[7] 颜伟，田甜，张海兵.考虑相邻时段投切次数约束的动态无功优化启发式策略 [J].电力系统自动化，2008，32 (10)：71-75.

[8] 阮仁俊，何冰，孔德诗，等.锦标赛蚁群算法在无功优化中的应用研究 [J].电力系统保护与控制，2010，38(12)：80-85.

[9] 王韶，周鑫.基于层次聚类法和蚁群算法的配电网无功优化 [J].电网技术，2011，35(8)：161-167.

[10] 崔逊学.多目标进化算法及其应用 (第一版)[M].北京：国防工业出版社，2006：121-123.

[11] 程彬，刘芳，颜伟，等.动态无功优化的混合智能算法[J].重庆大学学报，2007，30(1)：22-27.

[12] 许有方.华中电网500 kV枢纽变电站的有载调压变压器和静止无功补偿器 [J].电网技术，2003，27(6)：68 -70.

Dynamic Reactive Power Optimization Based on Ant Colony Clustering Algorithm

ZHOU Xin1，XU Shoudong1，DUAN Xiao2，GU Ying2
(1.Yunnan Electric Power Research Institute，Kunming 650217；2.State Grid Nanyang Electric Power Company，Nanyang，Henan 473000)

The conception of unnecessarily action time(UAT)is proposed，which unification considered the distribution changes of system’s load rate，to make sure the movement number of times of equipment meet the request.Cluster ant colony optimization algorithm is proposed，which the cluster algorithm and ant colony optimization algorithm(ACOA)are united.According to systematic change，this method cans adjustment the information of the paths.And the conception of Path diversity is proposed，which can prevent excessive accumulation of pheromones and decrease algorithm searches for number of times.The feasibility，validity and effectiveness of the algorithm are verified by the results of IEEE 14 bus and IEEE 30 bus distribution system.

dynamic reactive power optimization；unnecessarily action time；cluster ant colony optimization algorithm；path diversity

TM76

B

1006-7345(2014)05-0040-07

2014-01-26

周鑫 (1984)，男，硕士，助理工程师，云南电力试验研究院，主要从事励磁、保护研究工作 (e-mail)zhouxin8421＠126.com。

许守东 (1979)，男，硕士，高级工程师，云南电力研究院，主要从事保护及自动化研究工作 (e-mail)741698897＠qq.com。