基于NSGA-II的多目标设备动态布局方法

黄君政，李爱平，雷 明

（同济大学 机械与能源工程学院，上海 201804）

全球制造业竞争日益激烈，一个高效的生产系统对于增强企业的竞争力至关重要，其中车间设备布局（Facility Layout，FL）是制造系统设计的重要内容.合理的设备布局可以提高生产效率，降低生产成本，缩短产品周期.研究表明，大约20%～50%的加工费用于物料运输，而合理的设备布局至少能节约10%～30%的物流运输费用［1］.

近年来市场需求的最大特点就是多样化，即需求的动态性及其导致的生产计划的动态性.一旦客户需求发生变化，车间内部不变的静态设备布局（Static Facility Layout，SFL）往往难以符合新的生产计划.当制造系统需要发生变化且未来产品需求可预测时，需要制定基于一个时间段的设备布局方案，即由每个时期一个布局方案组成一系列的设备布局方案，这就产生了动态设备布局问题（Dynamic Facility Layout Problem，DFLP）.ROSENBLATT［2］于1986年首先提出DFLP的模型和最优解，此后又有大量学者对其进行了研究.

目前，对动态设备布局问题的研究大多按离散情况建立模型，主要研究如何将n个不可分割的等面积设备合理有效地安排在n个位置上，通常采用二次分配问题（Quadratic Assignment Problem，QAP）进行描述.但此方法有一定局限性，例如，在实际生产中设备的面积与设备间的间隙通常不同，车间中可安放设备的位置有一部分无法预先确定.近年来大量学者对更符合实际情况的设备布局连续模型进行了研究，并取得了很好的效果.连续模型是将车间看成连续的平面，确定不等面积设备的精确位置.但连续模型目前大多用于静态设备布局问题，在动态设备布局问题上的应用较少.

布局问题的优化目标主要集中在减少距离、时间或成本.随着布局的深入研究，发现单一目标并不能很好地实现整体效益，因此越来越多学者开始研究多目标的布局问题.动态车间布局优化目标有定量目标和定性目标，包括物料搬运成本最小［3］、布局重组成本最小和车间面积利用率最大［4］等.多目标优化方法主要有多目标单一化法和基于Pareto的寻优法两种［5］.前者具有系数难以确定，容易出现早熟的缺点，而基于Pareto寻优的方法直接在多目标空间内寻优，不需要将多个目标进行转化，得到一组Pareto解集.在基于Pareto寻优的多目标优化算法中，DEB［6］在2002年提出的带精英策略的非支配排序遗传算法是一种有效的算法，已被国内外广泛用来求解多目标优化问题.

基于以上分析，本文针对车间布局问题的动态性和多目标性的需求，选取了物流及重布局费用、非物流关系和面积利用率3个优化目标，建立了多计划期的车间内不等面积设备的连续模型，并利用NSGA-II对其求解，得到Pareto解集，获得车间整个生产计划期内最优的一系列设备布局方案集，以供决策者优中选优.

1 设备动态布局多目标优化模型

动态设备布局问题是在未来r个生产计划期可预测的前提下进行布局规划的，根据各子计划期工序间物流矩阵等约束条件的变化，调整各期设备布局方案，针对选取的物流及重布局费用、非物流关系和面积利用率3个目标进行优化.

1.1 问题描述

对于具有r个确定计划期的动态布局问题，每一期均可看作静态设备布局问题，在布局时做出如下假设：

（1）布局车间和各设备均为矩形结构，车间大小和设备尺寸均已知，忽略其细节形状.

（2）各设备分行排列，平行于车间水平边（x轴）放置，且设备之间水平间距要求已知.

车间设备布局图如图1所示.多行连续型设备布局问题的数学模型的相关参数及各参数间的关系如图1所示.图1中，mi，mj分别为设备i、设备j，li，lj分别为设备i、设备j的长度；wi，wj分别为设备i、设备j的宽度；hij分别为设备i、设备j之间的水平最小间距要求；mo，lo，wo分别为第1行设备及其长度、宽度；v为设备行间距；v0为第1行设备到车间下边界的距离.x（t）i，x（t）j分别为在子周期t内设备i、设备j的中心点的x轴坐标；y（t）i，y（t）j分别为在子周期t内设备i、设备j的中心点的y 轴坐标；x（t）0，y（t）0分别为在子周期t内第一行设备的x，y轴坐标.

（3）子周期间设备重置移动距离为设备中心的折线距离，子周期t与t＋1间设备i的移动距离如图2所示.

图1 车间设备布局图Fig.1 Workshop facilities layout

图2 子周期之间设备移动的矩形关系Fig.2 Moment relations of facilities between son-perids

1.2 优化目标及数学模型

本文将优化目标分为费用目标和非费用目标.费用目标包括物流费用、布局重置费用；非费用目标包括非物流关系、面积利用率.具体分析如下：

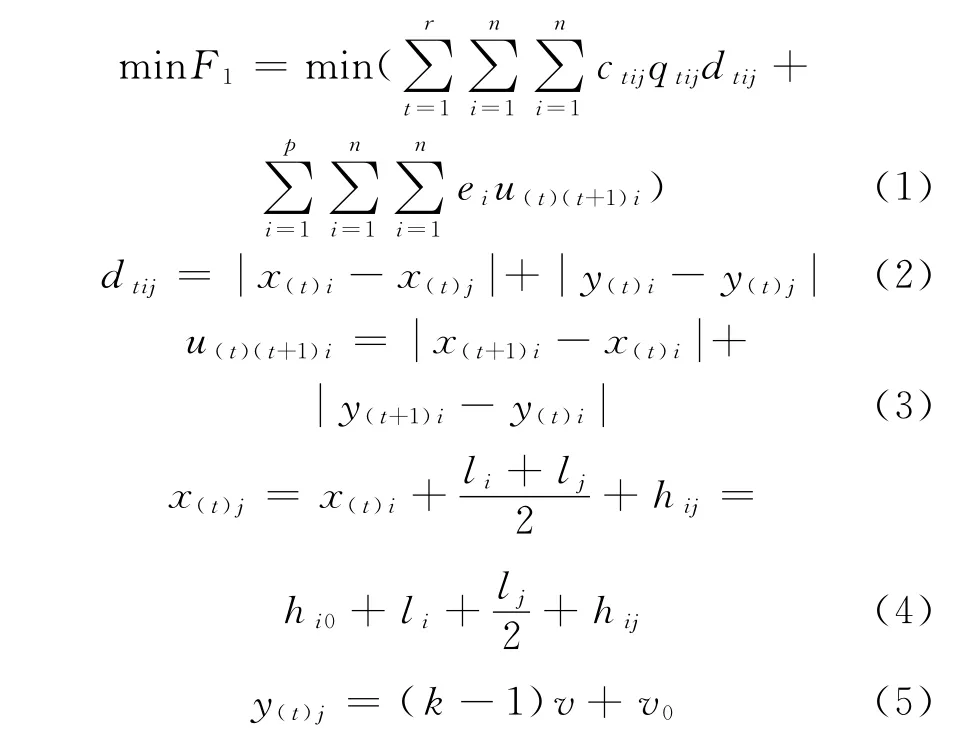
（1）物流及重布局费用最小化.其中物流及重布局费用是整个计划期中物料运输费用和相邻计划期之间的重布局费用之和.具有r个计划期，需对n台设备进行布局的DFLP问题的物流及重布局费用如式（1）—（5）所示.式中：F1为所有计划期总费用；r为计划期总数；n为车间内需进行布置的设备数量；ctij为自计划期t内设备i与设备j之间的单位物料单位距离的搬运费用；qtij为在子计划期t内设备i和设备j之间物料搬运频率；dtij为在子计划期t内设备i和设备j之间的物流搬运距离，即设备中心点之间的折线距离；ei为从设备i每单位距离的移动费用；u（t）（t＋1）i为在子计划期t与（t＋1）之间设备i距离移动的距离.hi0为设备i与车间边界的水平最小间距要求；子计划期为t时，位于第k行的第1个设备i，其相邻的设备j所摆放的坐标由式（4）和式（5）计算.子周期t和t＋1间设备i移动的矩形距离，模型的参数和参考线见图2.

（2）非物流关系最大化.根据LEE K［7］等人研究提出的非物流关系表达方法，针对多计划期进行修改，本文模型的非物流关系可表达为

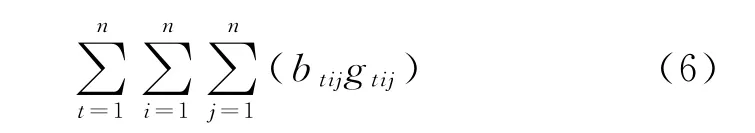
式中：gtij为设备之间的非物流密切度值，如表1所示；btij是布局方案中设备之间的密切度关联因子，它由资源间的实际物流距离dij和最大可能距离dmax决定，如表2所示.

非物流关系的值越大，表明非物流关系越密切，为方便利用NSGA-II编程解决多目标布局问题，非物流关系目标函数F2如式（7）所示.

表1 设备关系密切度分类Tab.1 Facilities relations classfication

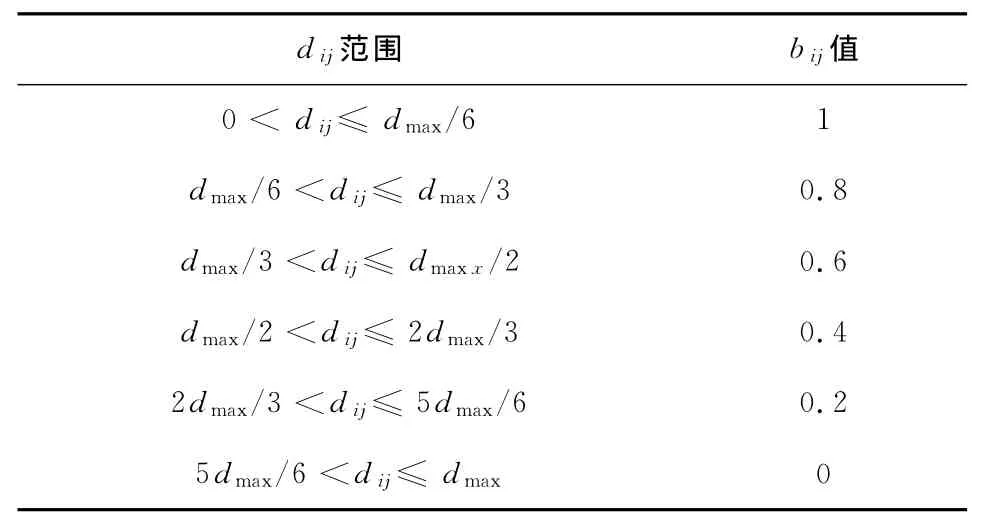
表2 密切度关联因子Tab.2 Factors of facilities relations

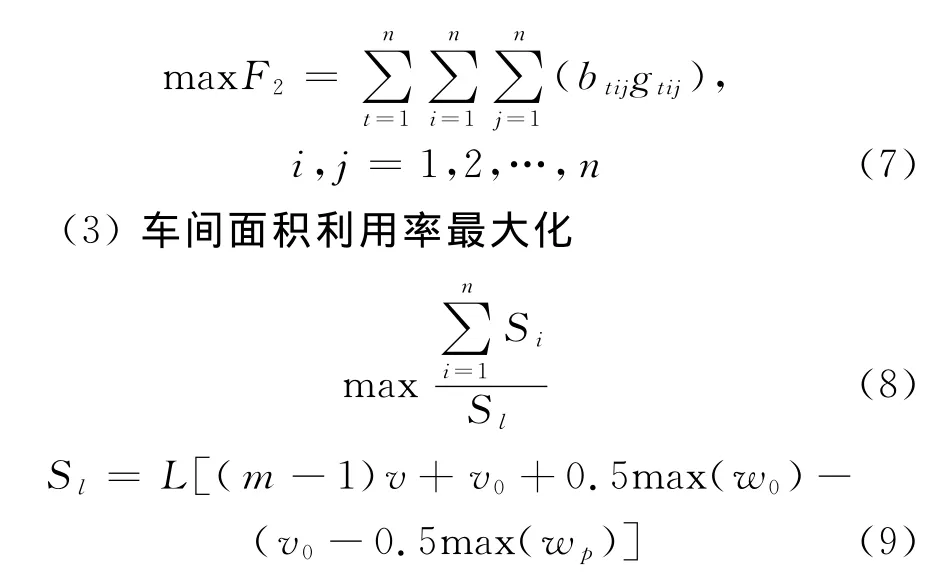
式中：Si为设备i的占地面积；Sl为由布局方案包络矩形的总面积；L为车间的长度；m 为设备布局的总行数；w0为最后一行上的设备的宽度，wp为第一行上的设备的宽度.又因Si为设备i的占地面积，Si之和为常数，故目标函数F3车间面积利用率最大化也可以表示为

2 优化算法设计

2.1 NSGA-II算法

本文采用DEB［6］提出的NSGA-II算法求解已建立的优化模型，NSGA-II算法过程如图3所示.

步骤1 t＝0，初始化种群P0，种群规模为N，对P0进行非支配排序（rank）及拥挤度（distance）计算.

图3 NSGA－Ⅱ算法流程图Fig.3 Flow chart of NSGA-Ⅱ

步骤2 根据P0中个体的非支配排序值及拥挤度大小进行选择操作，经过交叉及变异后产生规模为N的子种群Q0.

进行步骤3至步骤7的迭代，直至t＝maxgen，maxgen为最大迭代次数.

步骤3 合并Pt和Qt，形成规模为2 N的种群Rt.

步骤4 对Rt进行非支配排序，得到k个非支配解集F1，F2，…，Fk，其中F1为最优非支配集，F2为次优非支配集，依次类推.

步骤5 从F1开始依次取基因个体直至总数超过N个，假设此时的非支配解集为Fi.

步骤6 由于F1，F2，…，Fi中的个体数量之和大于N，则对Fi中的个体进行拥挤度计算.选择Fi中较好的个体和F1至Fi－1中的全部个体一起组成规模为N的新种群Pt＋1.

步骤7 对新种群Pt＋1进行选择，交叉及变异，形成Qt＋1，返回步骤3.

如此反复迭代直至达到最大迭代次数，即可得到优化结果.

根据车间设备动态布局多目标优化模型的特点，本文设计了NSGA-II算法的染色体编码、交叉、变异及罚函数，具体分析如下：

（1）染色体编码

染色体编码表达选用解决连续参数优化问题普遍适用的实数编码方式，在此处选用设备编号.将一个布局或方案描述为一个二维矩阵，每列代表单个自计划期内的布局方案，列数地表所需布局的设备数量.某具有r个自计划期，需布置n台设备的车间设备动态布局的染色m 应该表达为一个n×r的矩阵：

采用动态分行技术来对各设备进行布局设计，若在同一行内的各设备长度及其设备相互间距之和超过了布局车间的长度，则该行最后一台设备自动进入下一行.

（2）交叉

用部分映射交叉（Partial Mapped Crossover，PMC）方法处理设备排列序列的交叉操作.PMC方法为随机选取两个交叉点，两个交叉点之间的部分逐个交叉.用算数交叉的方法处理净间距序列.

（3）变异

交叉运算已从全局的角度搜索到接近最优的编码结构故仅对设备净间距序列进行变异操作，使染色体从局部角度逼近最优.，根据变异概率pm，随机选择染色体中的某个净间距进行变异，变异后的净间距仍在［Δmin，Δmax］之间.

（4）罚函数

由于采用自动换行策略，在x方向上不会产生重叠的不合理解.只需保证在y方向上最后一行的设备放置在车间尺寸范围内即可，P为y方向超出车间区域的惩罚项，如式（15）所示.wi为最后一行上设备的宽度，H为车间的宽度，T为正的大数惩罚项.如式（12）所示.

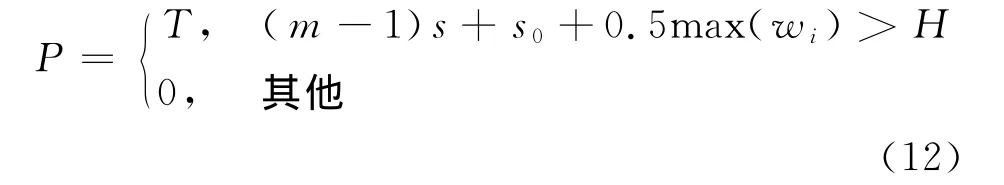
对于每个染色体，在利用NSGA-II进行非支配排序时，目标1和目标3的值加上P，目标2的值减去P.因目标1和目标3以最小值为优化目标，目标2以最大值为优化目标，故不合格的染色体会因目标值1和目标值3太大或目标值2太小而被淘汰.

3 实例研究

3.1 实例描述

某柴油发动机厂拟新建一缸体加工车间，该车间长×宽＝14m×12m，需对12台加工设备进行布局，设备尺寸如表3所示.设备之间的距离矩阵为Hij（式12），设备行间距v＝2.5m；第1行设备距车间边界距离v0＝1.0m；各设备与车间左右边界距离相同，分别是［11.21.51.11.21.11.21.31.41.31.21.5］；本文考虑该车间有3个计划期的情况，生产计划分别为：第1期生产A产品4300件B产品1000件、C产品2400件；第2期生产A产品1600件、B产品0件、C产品5500件；第3期生产A产品200件、B产品5800件、C产品500件.根据该企业实际情况，并分析各加工设备间的物流量和非物流关系，可得各计划期内各设备间的物流强度汇总如表4所示.设备间搬运费用矩阵为Cij（式13），非物流关系密切度为Gij（式14），重布局时，各个设备单位距离的移动成本矩阵 Mi为：［1.71.61.81.42.21.61.81.61.91.72.11.6］.

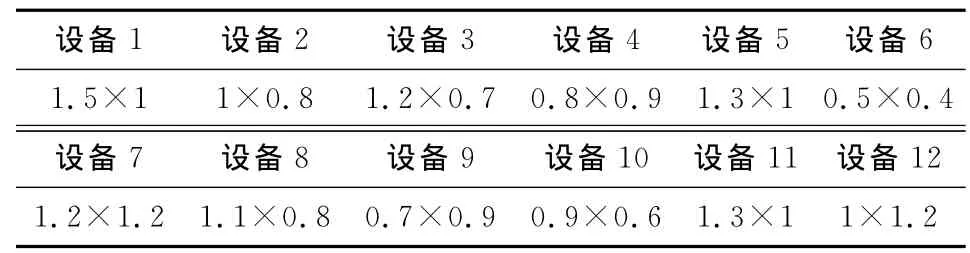
表3 设备尺寸 单位（m×m）Tab.3 Dimensions of facilities

表4 设备间物流强度汇总Tab.4 Logistics intensity between facilities

优化过程中遗传算法的参数如下：种群数量N＝100；最大遗传代数MAXGEN为100；交叉概率因子pc＝0.7；变异概率算子pm＝0.2；惩罚函数P中的常数值T＝500.以式（1），（7），（10）作为优化目标，运用MATLAB编程，对此3×12实例问题进行优化计算，所得到的Pareto解集如表5所示.其中方案f的目标1最优，方案a的目标2最优，方案d的目标3最优.不存在某个染色体能使得3个目标同时达到最优.

表5 Pareto解集Tab.5 Pareto optimal set

3个目标的平均值和最小值随遗传代数的进化过程图如图4，5，6所示.

图4 目标1的进化过程Fig.4 Evolution process objective 1

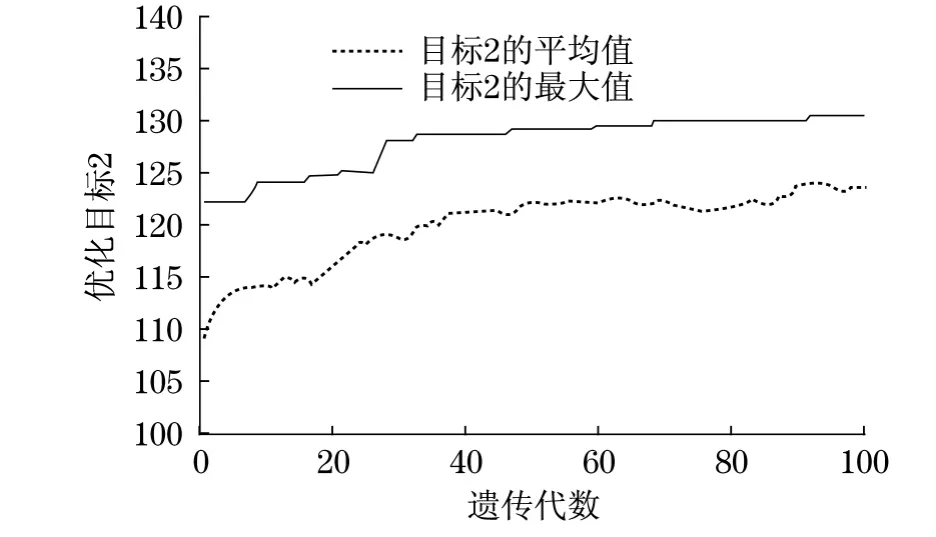
图5 目标2的进化过程Fig.5 Evolution process objective 2

图6 目标3的进化过程Fig.6 Evolution process objective 3

利用NSGA-II算法，可保证目标函数1，3的平均值和最小值，随遗传代数的增加，均保持总体下降的趋势，目标函数2的平均值和最大值随遗传代数的增加，保持总体上升的趋势.充分说明了NSGA-II算法可使多个目标同时优化.图6中，从目标3的平均值进化曲线中可发现当遗传代数为40代至100代时，目标3的平均值出现了较大的波动，这也表明了NSGA-II在寻求多目标函数全局的最优解时，会偶尔以目标3的增大作为代价.

4 结语

本文研究了在企业产品需求可预测的情况下，具有多个产品计划期的设备动态布局问题的连续模型，根据多个优化目标，采用NSGA-II算法求解优化模型，克服了传统加权法求解多目标问题的缺点.通过生物进化原理，不断进化得到优秀个体集（Pareto解集）以供决策者优化抉择.案例分析验证了模型与算法的可行有效，为实际企业多目标的动态布局问题提供了一个行之有效的方法.

［1］BRAGLIA M，ZANONI S，ZAVANELLA L.Layout design in dynamic environments：strategies and quantitative indices［J］.International Journal of Production Research，2003，41（5）：995－1016.

［2］ROSENBLATT M J.The dynamics of plant layout［J］.Management Science，1986，32（1）：76－86.

［3］AMIR S.A genetic algorithm with the heuristic procedure to solve the multi-line layout problem ［J］.Computers ＆Industrial Engineering，2012，62（4）：1055－1064.

［4］余世根，鲁建厦.基于GA固定约束条件下多目标车间设备布局问题研究［J］.浙江工业大学学报，2010，38（4）：401－405.YU Shigen，LU Jiansha.Research on multiple facilities layout problem based on GA fixed constraints［J］.Journal of Zhejiang University of Technology，2010，38（4）：401－405.

［5］玄光男，程瑞伟.遗传算法与工程优化［M］.北京：清华大学出版社，2003.XUAN Guangnan，CHENG Ruiwei.Genetic algorithm and angineering optimization［M］.Beijing：Tsinghua University Press，2003.

［6］DEB K.A fast and elitist multi objective genetic algorithm：NSGA-II［J］.IEEE Transaction on Evolutionary Computation，2002，6（2）：180－197.

［7］LEE K，ROH M，JEONG H.An improved genetic algorithm for multi-floor facility layout problems having inner structure walls and passages［J］.Computer ＆Operation Reseach，2005，32（4）：879－899.