控制力矩陀螺驱动的空间机器人轨迹跟踪控制
2014-03-16贾英宏徐世杰
贾英宏 赵 楠 徐世杰
(北京航空航天大学 宇航学院,北京 100191)
控制力矩陀螺驱动的空间机器人轨迹跟踪控制
贾英宏 赵 楠 徐世杰
(北京航空航天大学 宇航学院,北京 100191)
提出一种新的空间机器人设计概念,并研究其轨迹跟踪控制问题.系统中的各机械臂以自由球铰连接,在机器人平台和每节机械臂上均安装有一组控制力矩陀螺(CMGs,Control Moment Gyroscopes)作为控制力矩执行机构.采用改进的罗格里得斯参数(MRPs,Modified Rodrigues Parameters)描述平台和各节机械臂的姿态,利用Kane方程建立了系统的动力学模型.在此基础上,用逆动力学方法设计了系统的轨迹跟踪控制律,用以实现卫星平台的位置/姿态和机械臂末端作用器位置的轨迹跟踪控制.采用带有零运动的CMGs操纵律以使CMGs准确输出力矩并回避构型奇异.基于两关节机械臂系统和金字塔构型CMGs的数值仿真结果验证了所设计的控制律和操纵律的有效性,以及自由球铰连接方式在提高末端作用器运动自由度和降低系统动力学耦合方面的优越性.
空间机器人;控制力矩陀螺;球铰;轨迹跟踪控制;Kane方程
空间机器人在在轨服务中具有广阔的应用前景,其轨迹跟踪控制问题也一直是航天领域的热点问题[1].然而,目前工程上已应用的空间机器人均采用关节力矩驱动的方式,大多数理论研究也采用此类驱动方式.利用关节力矩驱动时,关节处的作用力矩/反作用力矩特性使得系统的动力学耦合显著,进而增大了各运动体精确轨迹跟踪控制的难度[2].
为降低或消除系统的此类动力学耦合,国外有学者提出了“无反作用执行机构(reactionless actuator)”的概念,即机械臂连接采用自由铰接方式,在各机械臂上安装角动量交换装置(飞轮或CMGs,Control Moment Gyroscopes)作为执行机构.由于机械臂铰接处无需施加控制力矩,因而关节处不存在直接的作用力矩与反作用力矩.这一设计概念最早由文献[3]提出,方案中机械臂以单自由度自由柱铰连接,每节机械臂上安装有一个反作用飞轮作为力矩执行机构.文献[4-5]中,首先将CMGs应用于单自由度柱铰连接的刚性机械臂系统,指出使用飞轮和CMGs减小了机械臂对平台的干扰力矩,并且CMGs相对飞轮具有显著的功耗优势.之后,Carpenter设计了由两只V字构型CMGs驱动的三柱铰关节机械臂系统,作为高精度高灵敏度空间望远镜的基座[6],并初步研究了该系统的能量最优控制问题[7-8].此后,文献[2,9-10]对V字构型CMGs驱动的自由柱铰关节系统进一步分析了不同运动情况下系统的功耗和动力学耦合程度问题.
以上研究为空间机器人的设计提供了新的思路.然而,在上述研究中,各机械臂仍然以柱铰连接,每个关节只有一个转动自由度,且CMGs仅限于两只陀螺构成的V字构型.本文对无反作用执行机构概念进行进一步扩展,提出基于自由球铰连接的设计概念,因而可用更少的关节提供更多的运动自由度.此外,不限定CMGs的具体构型,因而研究具有更广的适用范围.
针对所提出的设计概念,本文建立了适用于任意关节数系统的动力学模型,并研究了其轨迹跟踪控制问题.研究结果表明,两关节系统即可在平台位置/姿态稳定控制的条件下实现末端作用器三维位置轨迹跟踪,且平台姿态稳定控制力矩明显小于关节驱动系统,验证了自由球铰连接方式在提高机械臂运动自由度以及降低系统动力学耦合方面的优越性,同时也验证了所设计的系统控制律的有效性.
1 系统概念描述
本文所提出的空间机器人设计概念如图1所示.
系统由刚性平台和n节刚性机械臂构成,各机械臂之间以及机械臂与平台之间均以自由球铰连接.平台内部以及各机械臂上均安装有一组数量不少于3的CMGs,作为力矩执行机构.为描述方便,平台记为B0,各节机械臂由内而外依次记为 B1,B2,…,Bn.后续研究中对系统作如下合理假设[11]:
1)各CMG绕其框架轴转动时,CMG本身的质心位置不变,即运动体 Bi(i=0,1,…,n)相对其任一固连坐标系的静矩为常值;
2)各CMG绕其框架转动时,CMG转动对其安装运动体转动惯量的影响为小量,可以忽略,即运动体 Bi(i=0,1,2,…,n)相对其上任一固连坐标系的惯量矩阵为常值.

图1 系统设计概念示意图
此外,假定CMG框架伺服机构具有理想性能,因而研究系统级的动力学模型时研究对象为由平台和各节机械臂构成的多体系统,无需考虑CMG自身的动力学特性.在广义惯性力建模时每组CMGs视为相应的运动体的一部分,由假设条件可知,每一运动体均具有常值静矩和惯量.
2 系统运动学与动力学方程
为描述由平台和机械臂构成的系统运动,建立如图2所示的如下坐标系:
1)惯性坐标系FI(Oxyz),原点O可位于惯性空间任意一点,各坐标轴固连于惯性空间;
2)平台本体坐标系F0(o0-x0y0z0),原点o0可位于平台中任意一点,各轴与平台本体固连;
3)机械臂Bi体坐标系Fi(oi-xiyizi),原点oi位于Bi与其内接体的铰接点处,各轴与Bi固连.

图2 系统坐标系与位置矢量
将坐标系 F*(*=I,0,1,…,n)的各坐标轴单位矢量记为矢阵形式,其中和分别为坐标系F*三轴方向的单位矢量.利用矢阵的定义,任一三维向量xv可以表示为
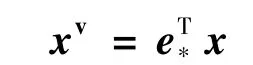
式中x∈R3×1为xv在坐标系F*中的分量列阵.
以 σi=[σi1σi2σi3]T表示Fi相对惯性系FI的 MRPs(Modified Rodrigues Parameters),则 σi与ωi存在如下的运动学关系[12]:

式中

其中,右上标“×”表示列阵的叉乘反对称阵;En为n×n的单位阵.
选取系统的广义速度列阵为

广义坐标列阵为
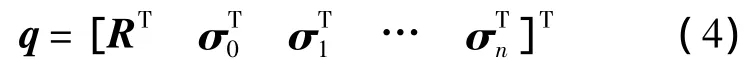
则广义速度与广义位移的运动学关系为

式中
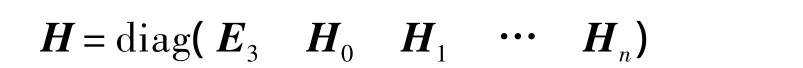
运动体Bi(i=0,1,…,n)的质量参考点速度矢量以及运动体Bi的角速度矢量可写为

式中,Gi∈R3×(3n+6)为运动体Bi的偏速度矩阵;Wi∈R3×(3n+6)为运动体Bi的偏角速度矩阵.对求时间导数,可得Bi的质量参考点的加速度矢量为

根据矩阵形式的Kane方程[13],系统的广义惯性力可写为
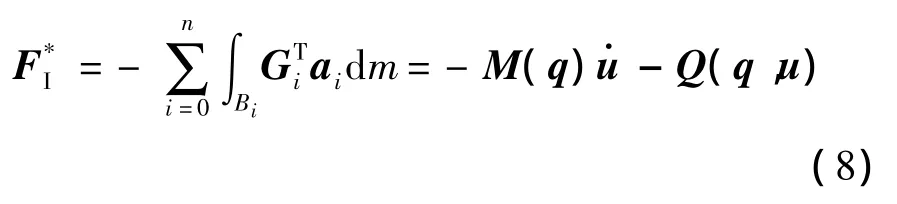



第2项为Bi的角速度引起的力矩输出项,记为

根据Kane方程,系统动力学方程为

将式(8)~式(10)代入式(13),系统动力学方程可整理为如下形式:

式中

其中

式(14)和式(5)共同构成了系统的运动方程.
3 系统控制律设计
为实现末端作用器的位置轨迹跟踪控制,同时考虑平台的位置/姿态控制,定义系统输出为

式中Rt为末端作用器在惯性空间中的位置.记为二阶可微的系统期望输出轨迹,为轨迹跟踪误差,则轨迹跟踪控制律设计目的可描述为
对式(15)求导可得

式中J∈R9×(3n+6)为雅可比矩阵.将式(5)代入式(14),经变换可得

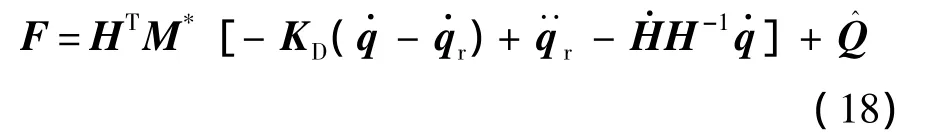
式中KD为正定阵,为可选控制参数;为的参考轨迹,取为
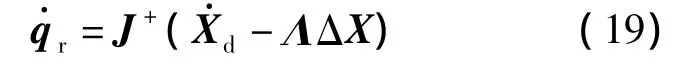
式中,J+=JT(JJT)-1;Λ为正定阵,为控制参数.
需要指出的是,在式(19)中已假定n≥2,即关节数不少于2.尽管理论上单关节球铰连接也可实现机械臂末端的三维轨迹跟踪(此时,式(19)的J+改为J-1,即q·的参考轨迹仅具有唯一解),但其可达轨迹仅限定为以球铰为圆心的球面,不具一般性,因此一般情况下球铰连接系统也至少需要两个关节.
为验证控制律的稳定性,将式(18)代入式(17),并在方程两端同时乘以(M*)-1可得

由 KD的正定性可知有.由式(16)和式(19)有,因而有由于 Λ为正定阵,因此有和,系统是渐近稳定的.
若系统中某输出(如平台位置/姿态)的期望轨迹设定为常值,则控制律使得系统的该输出收敛于期望值,即进行稳定控制.
4 CMGs操纵律
假定陀螺群i中的陀螺数量ni>3,为有效回避构型奇异,操纵律采用如下带有零运动的广义逆操纵律[14]:

式中
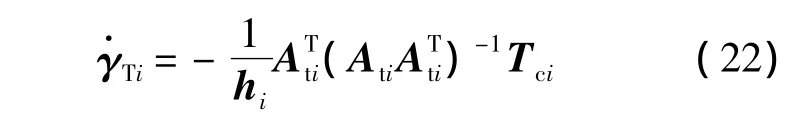
用以输出指令控制力矩,而

为零运动,用以回避奇异.式中λi为正的标量参数,)为陀螺群i的构型奇异度量.
5 数值仿真
数值仿真中所取的模型为如图3a所示的两关节模型.平台为边长为1.5m的立方体,机械臂B1和B2长度均为1.5m.坐标系F0原点位于立方体几何中心,各轴分别与立方体棱线平行.各臂的体坐标系z轴与臂杆的轴线方向一致.当F0与各臂体坐标系各轴指向一致时,系统构型如图3a所示.平台和各机械臂上均安装有4只CMG构成的金字塔构型力矩陀螺群,金字塔顶轴沿各体坐标系的z轴方向,每只CMG框架轴与塔顶轴夹角为 β =53.1°,如图3b 所示.
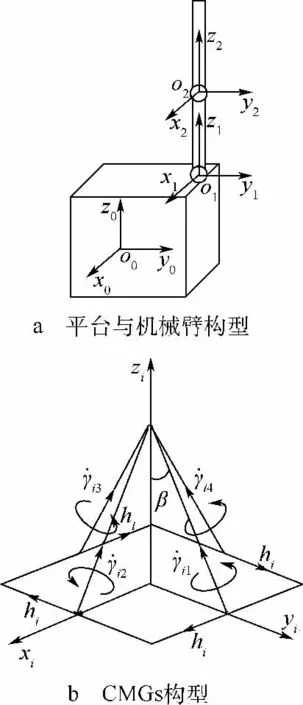
图3 仿真系统构型示意图
系统的质量特性参数如表1所示,其中各运动体的静矩和惯量均相对于其体坐标系定义.

表1 系统质量特性参数
系统中各安装点位置参数为

末端作用器位置参考点取为B2的端点,即
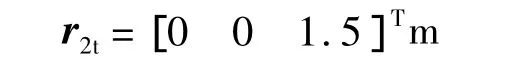
系统各广义速度初始值均取为零;各广义坐标初始值如表2所示.
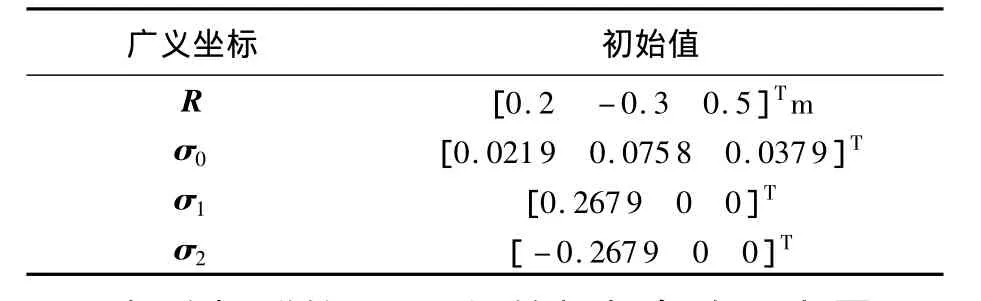
表2 系统广义坐标初始值
各陀螺群的CMG初始框架角均取为零,图3b所示即为CMGs框架角为零的初始状态.各陀螺群的CMG转子角动量为

平台的位置/姿态期望输出轨迹取为

即希望平台位置/姿态保持稳定控制.末端作用器的期望位置轨迹取为

其中

期望位置轨迹为一个圆心位于[z0y0z0],半径为r的圆轨迹.系统的控制参数取为
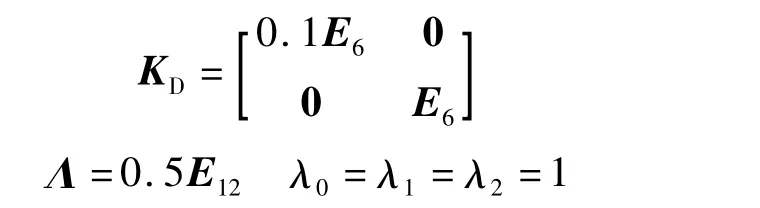
图4给出了系统位置跟踪误差ΔX以及速度跟踪误差Δ˙X的仿真结果,二者均在有限时间内收敛,且保持为零,验证了控制律的稳定性.图5给出了平台指令控制力FI0以及平台与各机械臂的指令控制力矩Tc0.由于机械臂末端作用器需要持续跟踪期望轨迹,因此平台姿态稳定后其指令控制力矩Tc0并不为零.平台指令控制力FI0虽然是大小连续可变的推力,但可通过脉宽调制的方法由推力器实现.

图4 系统跟踪误差
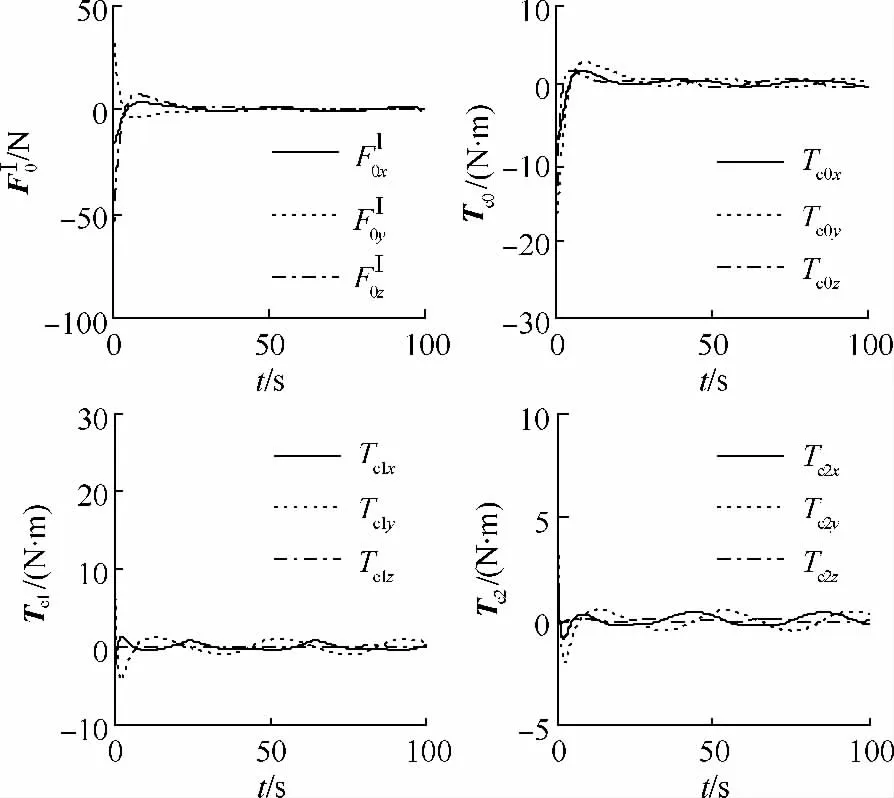
图5 系统指令控制力/力矩
仿真结果还表明,无论CMGs的操纵律中是否加入零运动,CMGs均能准确输出指令力矩,但CMGs的构型奇异度量不同.
图6给出了各组CMGs的构型奇异度量值.可见零运动可以有效增大奇异度量值,使CMGs远离构型奇异.
图7为系统在惯性空间中不同时刻的位置与构型状态.
图7中圆形轨迹为末端作用器期望轨迹,轨迹上的点为当前时刻末端作用器的期望位置.由所示运动过程可见,在平台本体位置/姿态稳定控制的同时,末端作用器逐渐接近期望位置.在30 s时系统控制已基本稳定,平台控制到了期望的零位置/零姿态状态,末端作用器也到达期望位置并跟踪期望轨迹.若利用传统的单自由度柱铰连接方式,则实现上述控制任务至少需要3个关节,因而球铰连接方式可有效减少关节数.
为验证CMG驱动系统相比关节驱动系统在降低动力学耦合方面的优越性,将两类系统进行了对比仿真,考察机械臂运动对平台的姿态干扰.仿真中平台初始位置/姿态均取为零,机械臂仍跟踪前述的位置轨迹,平台位置/姿态不控(即在控制律中将平台当前的位置/姿态作为其期望的位置/姿态).
图8给出了CMG驱动系统与关节驱动系统在控制过程中的σ0值,可见在相同的机械臂跟踪运动下,CMG驱动系统的平台姿态偏差明显小于关节驱动系统,验证了CMG驱动系统可以有效减小反作用力矩,降低系统动力学耦合.

图6 各组CMGs的构型奇异度量

图7 不同时刻系统位置与构型状态
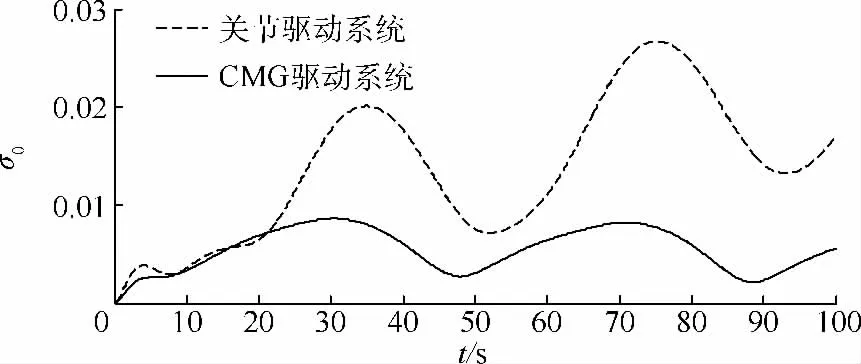
图8 CMG驱动与关节驱动系统的姿态偏差对比
6 结 束 语
为减小空间机器人系统的动力学耦合,同时利用较少的关节为机械臂提供更多的运动自由度,本文提出了一种CMG驱动的自由球铰连接空间机器人的设计概念.针对球铰关节具有3个旋转自由度且存在大范围旋转运动的特点,放弃传统的关节角的角位移描述方式,采用MRPs描述机械臂以及平台的姿态,并利用Kane方程建立了系统的动力学模型.在此基础上以平台位置/姿态和机械臂末端作用器位置为系统输出,利用逆动力学方法设计了轨迹跟踪控制器.采用带有零运动的CMGs操纵律来实现指令力矩和回避构型奇异.数值仿真结果验证了系统在提高机械臂运动自由度和降低系统动力学耦合方面的优越性,以及所设计的控制律和操纵律的有效性.
References)
[1] Xu W F,Liang B,Xu Y S.Survey of modeling,planning,and ground verification of space robotic systems[J].Acta Astronautica,2011,68(11/12):1629 -1649
[2] Brown D,Peck M A.Energetics of control moment gyroscopes as joint actuators[J].Journal of Guidance,Control and Dynamics,2009,32(6):1871 -1883
[3] Osuka K,Yoshida K,Ono T.New design concept of space manipulator-a proposal of torque-unit manipulator[C]//Proceedings of the33rd Conference on Decision and Control.Lake Buena Vista,FL:IEEE,1994:1823 -1825
[4] Peck M A,Paluszek M A,Thomas S J,et al.Control-moment gyroscopes for joint actuation:a new paradigm in space robotics[C]//1st Space Exploration Conference:Continuing the Voyage of Discovery.Orlando,FL:American Institute of Aeronautics and Astronautics Inc,2005:204 -233
[5] Peck M A.Low-power,high-agility space robotics[C]//AIAA Guidance,Navigation,and Control Conference 2005.San Francisco,CA:American Institute of Aeronautics and Astronautics Inc,2005:3759 -3770
[6] Carpenter M D,Peck M A.Dynamics of a high-agility,low-power coelostat telescope[C]//AIAA Guidance,Navigation,and Control Conference 2006.Keystone,CO:American Institute of Aeronautics and Astronautics Inc,2006:4175 -4191
[7] Carpenter M D,Peck M A.Minimum-power robotic maneuvering using control-moment gyroscopes[C]//AIAA Guidance,Navigation,and Control Conference 2007.Hilton Head,SC:American Institute of Aeronautics and Astronautics Inc,2007:210 -222
[8] Carpenter M D.Power-optimal steering of a space robotic system driven by control-moment gyroscopes[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Honolulu,HI:A-merican Institute of Aeronautics and Astronautics Inc,2008:7270-1-7270-15
[9] Brown D,Peck M A.Scissored-pair control-moment gyros:amechanical constraint saves power[J].Journal of Guidance,Control and Dynamics,2008,31(6):1823 -1826
[10] Carpenter M D,Peck M A.Reducing base reactions with gyroscopic actuation of space robotic systems[J].IEEE Transactions on Robotics,2009,25(6):1262 -1270
[11] Yoon H,Tsiotras P.Adaptive spacecraftattitude tracking control with actuator uncertainties[C]//AIAA Guidance,Navigation,and Control Conference 2005.San Francisco,CA:American Institute of Aeronautics and Astronautics Inc,2005:5311 -5322
[12]宿敬亚,张瑞峰,蔡开元.基于MRP的全局稳定的PID刚体姿态控制[J].航空学报,2011,32(4):710-719 Su Jingya,Zhang Ruifeng,Cai Kaiyuan.Globally stabilization PID attitude control of rigid body based on MRP[J].Acta Aeronautica et Astronautica Sinica,2011,32(4):710 -719(in Chinese)
[13] Banerjee A K,Kane T R.Largemotion dynamics of a spacecraft with a closed-loop,articulated,flexible appendage[C]//25th AIAA Structures,Structural Dynamics and Materials Conference.Palm Springs,CA:American Institute of Aeronautics and Astronautics Inc,1984:1 -37
[14]汤亮,贾英宏,徐世杰.使用单框架控制力矩陀螺的空间站姿态控制系统建模与仿真[J].宇航学报,2003,24(2):126-131 Tang Liang,Jia Yinghong,Xu Shijie.Modeling and simulation of attitude control for space station with SGCMG system[J].Journal of Astronautics,2003,24(2):126 -131(in Chinese)
Trajectory tracking control of space robot actuated by control moment gyroscopes
Jia Yinghong Zhao Nan Xu Shijie
(School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
A new design concept of space robotic system was proposed,as well as a trajectory tracking control approach.Unlike traditional manipulator arms,the space robot employs free ball joints as manipulator link connections.A group of control moment gyroscopes(CMGs),serving as torque actuators,was mounted on each link and the base.The modified Rodrigues parameters(MRPs)were employed to describe the attitude of the base and the links,and the equations of motion were derived by using Kane’s equations.To accomplish trajectory tracking control of both the base position/attitude and the end effector position,a control law was designed using the inverse dynamics method.A steering law with null motion was adopted for each group of CMGs to achieve simultaneous desired torque output and singularity configuration avoidance.The simulation results based on a two-joint space robot system with pyramid-configuration CMGs demonstrate the effectiveness of the proposed control law and steering law,as well as the ball joint advantage in increasing the degrees of freedom of the end effector and decreasing the system dynamical coupling.
space robot;control moment gyro;ball joint;trajectory tracking control;Kane’s equation
TP 242
A
1001-5965(2014)03-0285-07
2013-05-14;网络出版时间:2013-09-30 16:17;
10.13700/j.bh.1001-5965.2013.0259
www.cnki.net/kcms/detail/11.2625.V.20130930.1617.003.html
国家自然科学基金资助项目(11272027)
贾英宏(1976-),男,河北阳原人,副教授,jia_yingh@163.com.
