一种鲁棒的RSSI测距定位算法

程炳华,严筱永

(1.金陵科技学院计算机工程学院,江苏 南京 211169;2.金陵科技学院智能科学与控制工程学院，江苏 南京 211169)

无线传感器网络(Wireless Sensor Network,WSN)是一门集通信、微电子和传感器技术为一体的技术,具有广泛的应用领域,常常被应用在军事、医疗卫生、远程监控、抢险救灾等领域[1]。对于大多数应用,知道传感器节点的位置至关重要。有关研究表明传感器节点为用户所提供监测部署区域上下文相关信息,与位置信息有关占80%以上[2]。“低耗自主”[3]一直是WSN的基本特征,因此在全部节点加装GPS实现位置估计显然行不通,此外GPS仅适用于室外无遮挡条件下,因而在实际应用中,仅在部分节点上安装GPS,对于其他节点而言,其位置则需通过一定的算法估计出来。

目前,节点自定位算法常被分为基于测距和无须测距的定位算法两大类[4]。无须测距的定位算法相对简单,它利用路由跳数、网络连通性等信息进行定位,然而,其精度受网络拓扑以及信标节点密度等因素影响,因而误差也普遍较大。基于测距定位方法精度较高,但其精度受制于节点间的测量精度。最为常见的测距技术有RSSI、TOA、TDOA和AOA。RSSI测量数据可以在节点之间的每次数据交流中获取,并且不占有额外的带宽和能量,硬件花费相对简单和便宜[5]。这使得使用RSSI测量数据进行定位成为研究热点。然而基于RSSI测距的定位算法易受环境影响,定位精度不高,因此如何规避环境影响,提高定位精度是一个比较有意义的问题。

基于测距的定位算法一般分为两步,即:测距阶段和计算坐标阶段[5]。由于传感器节点常常部署在复杂环境中,且受到硬件老化、恶意攻击、电力不足、恶劣环境等因素的影响,使得在测距阶段获取的信号中含有较多误差,若不对这些误差采取有效抑制和处理,有时能产生±50%的测距误差[6],从而严重影响定位结果;此外信标节点分布[7]也会在一定程度上影响最终的坐标估计,使得计算坐标阶段估计不稳定。通过分析基于RSSI的定位技术存在的问题,提出一种新的鲁棒定位算法(robust location estimation,RLE),算法分别针对定位过程中的两个阶段,最大程度地减少误差和计算不稳定的影响,提高定位精度。

1 主要相关工作

1.1 测距阶段相关工作

在无线测距中,常用对数正态阴影模型作为节点间的距离测量方法[8]。其公式如下:

(1)

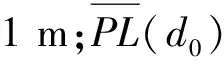
在实际应用中,RSSI信号总受到很多不稳定因素的干扰,在获得测距数据中不仅包含数量较多、幅度较小的测距误差(随机噪声),而且还包含少量幅度较大的测距误差(奇异点或粗差),在文献[9]中实验验证了RSSI这些干扰的存在。

随机噪声可以通过多次测量获取的均值来提高数据的精确度;而粗差则不能简单用统计均值的方法来消除其对精度的影响,因而对于最终的位置估计影响也最大。Huber[10]曾用含不同数量的粗差数据进行统计分析,当1 000个数据包含2个粗差时,足以使均值估计方法不可用。鉴于此,有关研究人员[11]借鉴概率论里的3 Sigma,通过选取高概率发生区的RSSI 值,然后再取其几何均值,这样处理是假设RSSI数值符合正态分布且假设粗差出现的比例不高的情况下,而实际环境下的RSSI数值并不符合正太分布,且出现的频率高于3 Sigma所假设的比例,因此定位估计使用此方法效果并不理想。Li[12]等研究人员利用中位数与最小二乘相结合的LMS估计对未知节点进行估计,LMS估计具有较高的鲁棒性和容错能力,这是因为中位数是拉普拉斯分布的极大似然估计,在理论上LMS可以抵抗含有50%的粗差的干扰。然而实际上包含粗差RSSI信号数据并不一定是执行错误所致,可能是固有的信号数据变异的结果,简单地剔除它们,有可能会导致重要的隐藏信息丢失,当然对待包含粗差的信号数据也不应当与正常数据一样对待,较为合理的做法是根据它们出现的分布概率,分别赋予相应权值以减少异常数据的影响。本文受到中位数抗噪思想的启发,结合实际情况,在测距阶段利用一种基于统计中值的加权测距方法,即在两节点之间通信交流一段时间,并获取一定数量RSSI数据后,在信号序列中,找到RSSI信号强度的中值,再对信号序列中每一信号强度都以此中值为基础计算其权值,最后让各个信号与相应权值相乘再求和,作为两节点之间的RSSI信号值并输出,然后再利用数正态阴影模型将其转化为相应的距离。

1.2 计算阶段相关工作

从理论上来讲,不属区域内信标节点越多,节点估计越精确。但事实上信标节点之间的几何分布以及信标节点与未知节点之间形成几何结构会很大程度上影响未知节点定位结果。如图1所示,未知节点U和信标节点B1、B2、B3的距离已知,由于3个信标节点近似在一条直线上,也就是说3点近似共线,那么未知节点U的估计位置就可能是U或者U′,此时无法确定U的实际位置。研究显示用于定位的3个信标节点组成的三角形完全共线时,仅仅简单地利用最小二乘法将导致最大的位置误差,可达200%[13]。

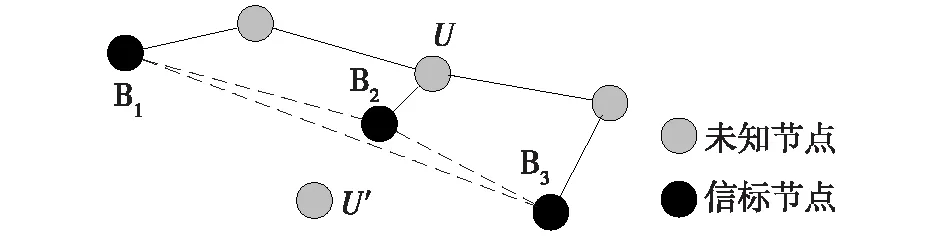
图1 信标节点近似共线Fig.1 Collinearity of beacon nodes

最小二乘法是一种无偏估计方法,具有局部最优的特点。目前,理论和实际工程中克服共线性影响的方法多样,研究人员提出了多种诊断方法和补救措施,其中最为常用且简单的方法是岭回归方法(Ridge Regression,RR)。岭回归由A.E.Hoerl[14]提出,通过引入偏移量k(又称为岭参数),以牺牲估计的无偏性换取估计方差的大幅减小,最终达到提高估计精度和稳定性的目的。对于估计模型ATAx=Ab,在引入岭参数k后,得到新的估计模型(ATA+kI)x=ATb。由于岭参数的引入使得位置估计不在是无偏的,但却解决了共线问题,使得估计值方差变小,同时使得估计变得稳定。岭回归方法简单易行,在一定程度克服了多重共线对估计值的影响,因而被广泛应用于工程实践中。岭回归方法的关键是如何选取合适的岭参数,岭参数的选择可以通过交叉检验获得,但其计算量较大,考虑到一般‖ATA‖<0.01为病态矩阵,因此本文设定k=0.01。

本文受此启发,在计算阶段引入岭回归方法,用它代替原先最小二乘法估计节点坐标方法。改进方法通过消除少部分有害信息以达到多重共线性,提高计算的稳定性,达到提高定位精度的目的。

2 RLE算法过程

针对测距和计算坐标阶段的不同性质的误差,分别采用一种基于统计中值的加权测距方法和RR方法改进了RSSI测距,进而提高了定位的精度。

J.W.Tukey[15]在1960年提出了一种接近实际的分布模型,其被称为污染分布,可表示为

f=(1-α)fg+αfo

(2)

其中,主体部分分布fg为正态分布,fo是干扰部分分布;α是污染率,表示污染部分所占比例。主体部分占据数据的主要部分,干扰部分是次要部分。对于正态分布,利用均值方法即可有效消除其误差;而对于干扰部分的分布,著名的鲁棒估计学者Huber[10]指出,许多干扰分布模式接近拉普拉斯分布,对于拉普拉斯分布,其极大似然估计是中位数,它是抗差能力最强的一种参数估计。受此启发,采用基于中位数加权的RLE算法,其具体过程如下。

1) 每个信标节点周期性的通过可控泛洪广播自身位置,在其有效通信半径内的未知节点收到该位置信息,在通信一段时间后,相应的未知节点得到相应信标节点RSSI信号序列。

2) 在每个RSSI信号序列中找到相应的中值Med_RSSI，可定义为:在获取的某个RSSI信号序列RSSI1,RSSI2…RSSIn中,先按数值大小排序,则信号序列的中值表示为

(3)

3) 式求信号序列中各个RSSI信号强度值在序列中相对应的权值。假设每个信号序列中有n个RSSI信号强度值,首先求每个RSSI信号值与中值的方差di;为了防止某些与中值相近的含粗差的信号的影响,在算法中加一阈值Thre,若方差大于阈值,则权值由方差决定;若方差小于阈值,则由阈值决定。每个序列中各个RSSI 信号的权值可按下式计算:

(4)

其中Thre可由下式表示:

(5)

其中,RSSIi为序列内第i个RSSI信号值。可以看出,RSSIi和Med_RSSI相差越大,相对应的加权系数越小,而Thre随着RSSIi和Med_RSSI方差而变化。

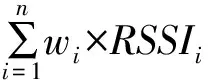
5) 式中未知节点在其通信半径内收到3个以上信标节点信号,则可以构造下列公式:

(6)

其中,(x1,y1),(x2,y2),…,(xn,yn)为信标节点坐标;(x,y)为未知节点。上述方程组可以转化为Ax=b的形式,其中：

(7)

当ATA可逆时,方程可以用最小二乘法求得未知节点估计坐标:

(8)

在实际部署时,用于估计位置的信标节点常出现共线或者近似共线现象,这时|ATA|=0或|ATA|≈0,即矩阵出现多重共线性现象,算法运用岭回归方法,则未知位置节点坐标

(9)

3 算法性能模拟与性能分析

节点定位的精度、功耗、适用环境与规模、信标节点比例、网络拓扑结构适应性、自适应和容错性等通常是评价定位方法常用的技术标准[11]。本文所提出的RLE算法主要针对定位过程信标节点位置关系和噪声对定位精度的影响,因此定位精度和信标节点比例是分析、评价的重点,因此,文中用方均根误差(Root Mean Square error,RMS) 这个具体性能参数指标考量算法的精度。RMS定义如文献[4]中所述。

仿真实验还需要配置另外一些参数,如:节点的通信半径,信标节点比例,粗差比例等。试验首先通过设置不同的信标节点比例比较改进RSSI算法与不考虑共线问题的RSSI定位算法。仿真实验假设节点分布在120*120区域,在此区域中随机部署200个节点,节点的通信半径设置为50,使用公式(1)作为RSSI信号值与距离关系的公式。同时为了降低随即部署场景中节点分布随机性对实验结果的影响,每种实验都进行了50次仿真,每次试验里节点都将重新随机分布在实验区域,统计每次的实验结果,并取均值作为评价依据。本文从两组实验对改进的RSSI进行考量,首先是假设信标节点一定,考量RMS随粗差比例变化,通过实验可以考察改进算法抗躁性是否鲁棒;其次是假设粗差比例一定,考量RMS随信标节点个数的增加的变化,信标节点个数出现越多共线的机会越大,通过实验可以考察出改进算法是否稳定。

实验1:设定信标节点从10开始逐渐增加到20,粗差比例为9%。由于噪声和信标节点拓扑质量等原因使得均值算法的RMS数值曲线呈上下起伏状,可以看出其定位效果较差且不稳定;利用3sigma方法去除了部分的粗差影响,但是仅去除了部分粗差,且3sigma方法并没消除共线的影响,因此从图2(a)看出RMS数值曲线同样呈上下起伏状,有时因为拓扑质量极差3sigma的RMS甚至比均值算法的RMS还高;而RLE算法通过对定位数据重新构造,将有用信息与噪声、共线信息重新排队,通过设定一定的阈值去除共线信息,使得RLE算法的RMS曲线随着信标节点增加而减小,且RLE算法的RMS都比相应的其他两种算法RMS低不少,其中RLE算法的平均RMS数值比3sigma方法低了约8.7%;而比均值方法低了约40.2%。

实验2:统计学家长期研究发现粗差存在的比例为1%～10%[10]。因此设定粗差设定为1%～10%,同时设定信标节点数为16。从图2(b)中看出均值算法和3sigma方法随粗差比例增长其两者RMS曲线急剧增大,且当有信标节点共线时3sigma的RMS数值可能大于均值算法,可以看出这两种算法对粗差很敏感且算法很不稳定;而RLE算法的RMS值相对较为低,RMS曲线缓慢增长,可以看出RLE算法对粗差不敏感且算法较为稳定。从图3可以看出,RLE算法的平均RMS数值比3 sigma方法低了约4.7%;而比均值方法低了约33.7%。

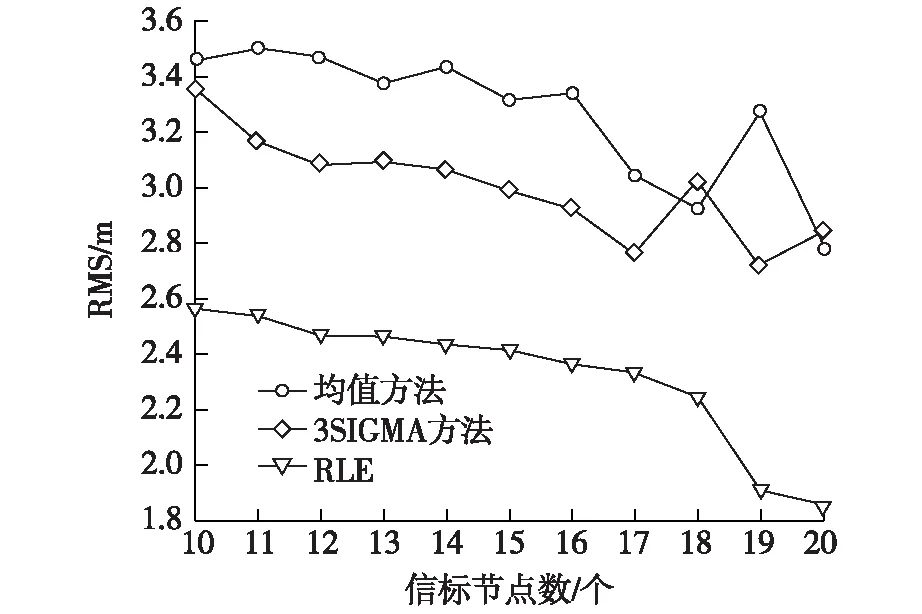
(a)随信标点数量变化的方均根误差

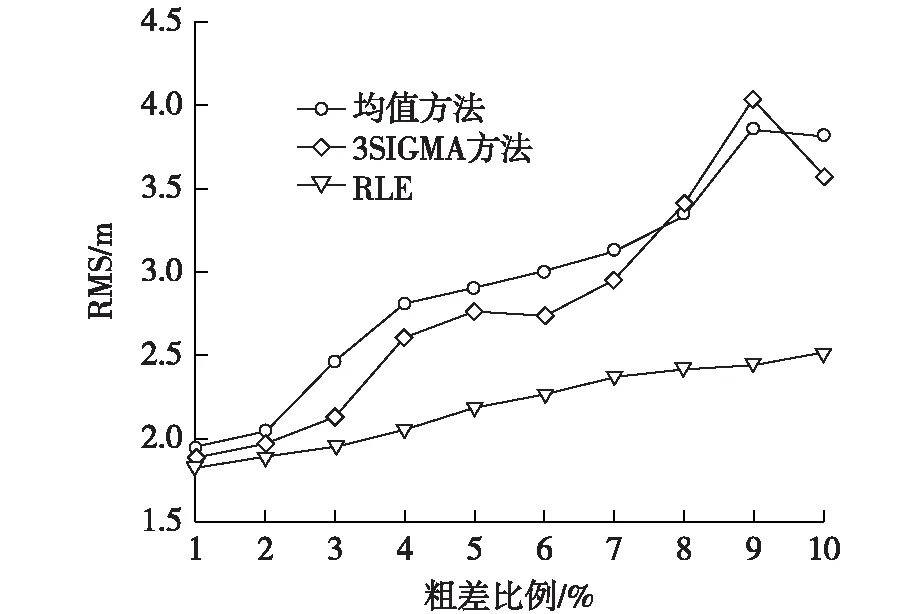
(b) 随粗差比例变化的方均根误差

4 结 论

文中针对RSSI定位算法的定位精度受到多种测距误差和信标节点拓扑影响这一现象,在其定位过程中首先利用统计中值的加权测距方法消除部署环境中测距信号误差的影响,而后在此基础上用基于岭回归回归方法消除共线所造成影响。RLE算法从实验结果来看较原先的估计方法更稳定,精度更高。同时也可以看出,本文所提的算法思想不仅仅在基于RSSI测距的位置估计算法中可以适用,也可以在其他的测距定位的算法中使用,作为其提高精度和稳定性的优化策略。

[1] Zheng J,Jamalipour A.Wireless Sensor Networks:A Networking Perspective[M].Hoboken:A John & Sons,Inc,2009

[2] 周艳.智能空间中定位参考点的优化选择及误差分析[D].沈阳:东北大学,2009

[3] 倪明选,李明禄,薛广涛.无线传感器的基础理论及关键技术研究[C].北京：清华大学出版社,2008,384-413

[4] 窦如林,阎浩,严筱永.基于偏最小二乘的无线传感网络多跳定位算法[J].金陵科技学院学报,2014,30(3):19-25

[5] Mao G,Fidan B.Localization Algorithms and Strategies for Wireless Sensor Networks:Monitoring and Surveillance Techniques for Target Tracking[M].New York:Information Science Reference,2009

[6] Liu Y,Yang Z.Location,Localization,and Localizability Location-awareness Technology for Wireless Networks[M].New York:Springer,2011

[7] 严筱永,钱焕延,高德民,等.一种基于多重共线性的三维DV-Hop定位算法[J].计算机科学,2011,38(5):37-40

[8] 孙佩刚,海赵,罗玎玎,等.智能空间中 RSSI 定位问题研究[J].电子学报,2007,35(7):1240-1245

[9] 赵方,马严,罗海勇,等.基于顽健估计的室内节点定位算法[J].通信学报,2008,29(11):113-120

[10] Huber P J,Ronchetti E M.Robust Statistics[M].2nd ed.New York:Wiley,2009

[11] Zhang C,Zhou X,Gao C,et al.On Improving the Precision of Localization with Gross Error Removal[C].28th International Conference on Distributed Computing Systems Workshops,2008:144-149

[12] Li X,Hua B,Shang Y,et al.A Robust Localization Algorithm in Wireless Sensor Networks[J].Frontiers of Computer Science in China,2008,2(4):438-450

[13] Tian S,Zhang X,Wang X,et al.A Selective Anchor Node Localization Algorithm for Wireless Sensor Networks[C].ICCIT Proceedings of the 2007 International Conference on Convergence Information Technology,2007:358-362

[14] Ae H.Application of Ridge Analysis to Regression Problems[J].Chemical Engineering Progress,1962,58:54-59

[15] J W Tukey.A Survey of Sampling from Contaiminated Distributions[M].California:Stanford University Press,1960