一类带有时间平均的随机偏微分方程
2014-03-15王丙均袁明霞
王丙均,袁明霞
(1.金陵科技学院公共基础课部,江苏 南京 211169; 2.南京大学金陵学院基础部,江苏 南京 210089)
尽管有效市场假说说明所有可以用到的信息都反映在股票当前时刻的价格中,以前的股票价格的各种波动不会带来什么信息,然而股票的一些统计信息,确实可以反映股票的一些行为。Kloeden and Lorenz[1]研究了如下的随机微分方程
d(x(t))=f(t,x(t),Ex(t),Ex2(t))dt+g((t,x(t),Ex(t),Ex2(t))dW(t)。
即方程的解的不仅仅依赖于自身而且依赖于其期望和二阶矩,见文献[2—3]。但是期望和二阶矩这些数字特征不容易得到。所以这些年来,带有时间平均的随机微分方程在金融模型中的应用吸引了越来越多的关注,因为时间平均非常易于得到,实用性很强。这类问题的一些研究成果可以在文献[4-10]找到。例如文献[10]研究了带有时间平均的随机微分方程
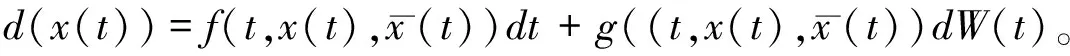

1 预备知识
令(U,‖‖U),(H,‖‖)分别为可分的希尔伯特空间;L2(U,H)为所有的从U到H的Hilbert-Schmidt 算子构成的空间;W(t),t≥0为定义在概率空间(Ω,F,P)上的一个U值柱形布朗运动;Ft,t≥0为(Ω,F,P)上自然域流。记为 ‖‖L2:=‖‖L2(U,H),‖‖:=‖‖H。
带有时间平均的无穷维随机偏微分方程

(1)
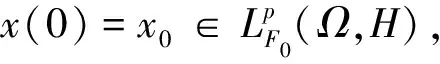
‖S(t)‖≤M
(2)
引理1[11]假设 φ(t),t≥0为一个 L2(U,H)值可料过程,则对与任意的p≥2,存在常数 C(p,T)>0,使得
2 温和解的存在性和唯一性
为了证明温和解的存在唯一性,做出如下假设,形式上和传统的李普希兹条件和线性增长条件类似。
(H1)(李普希兹条件) 存在一个正的常数k使得对于所有的x,x1,y,y1∈H和t∈[0,T],有
‖f(t,x,y)-f(t,x1,y1)‖∨‖g(t,x,y)-g(t,x1,y1)‖L2≤k(‖x-x1‖+‖y-y1‖)
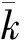
定义H值的过程x(t),t∈[0,T] 称为是(1)的温和解,若其对每个t∈[0,T],满足


(3)

证明首先,假设x(t)是方程(1)的一个温和解,初值为x(0)=x0。来证明(3)的正确性。
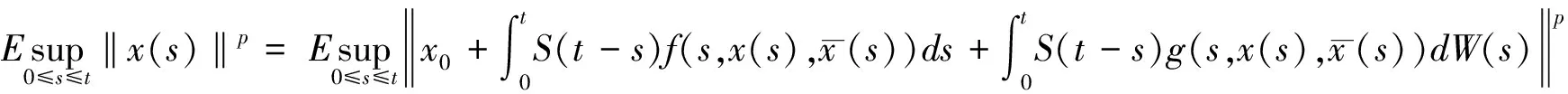
利用引理1,Holder不等式,(H2),Jensen不等式 和(2),有
利用Gronwall’s 不等式,得

接下来,将证明方程的温和解的存在性和唯一性。
定义一个空间Π,其上的范数记为‖‖Π,

(4)
其中α>0。可以验证Π是一个Banach空间(见[10])。注意到由(4),可以得到
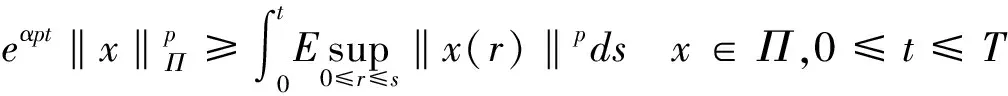
(5)
对x∈Π定义算子
要证明方程(1)的温和解的存在唯一性等价于寻找算子Ψ在Banach空间Π中的不动点。
令x(t)∈Π,和(3)的证明类似,有

利用(5)得
所以Ψ:Π→Π。
接下来将证明Ψ:Π→Π是一个压缩算子。令x,y∈Π,由引理1,Holder 不等式,(H1),Jensen 不等式和(5),有
其中b=(4T)p-1Mpkp+4p-1MpkpC(p,T)。
则
其中
显然,ρ(α)>0和 ρ(∞)=0,选取 α充分的大,使得 ρ(α)∈(0,1),则可以得到
‖Ψx-Ψy‖Π≤ρ(α)‖x-y‖Π
这说明Ψ:Π→Π是一个压缩映射,由Banach不动点定理,存在唯一的x(t)∈Π,使得Ψx(t)=x(t),t∈[0,T],这就是方程(1)的温和解。
3 结 语
本文在Yin和Wu工作的基础上[10],将有限维空间中带有时间平均的随机微分方程,推广到无穷维空间中,且为随机偏微分方程。在参数满足一定的条件下,证明了温和解的存在唯一性。
[1] Kloeden P E,Lorenz P.Stochastic Differential Equations with Nonlocal Sample Dependence[J].Bol Soc Esp Mat Apl,2010,51:99-108
[2] Scheinkman J,Lebaron B.Nonlinear Dynamics and Stock Returns[J].J Bus,1989(62):311-337
[3] Akgiray A.Conditional Heteroscedasticity in Time Serious of Stock Returns:Evidence and Forecasts[J].J Bus,1989,62:55-80
[4] Ficak B.Point Delay Methods Applied to the Investigation of Stability for a Class of Distributed Delay Systems[J].Systems Control Lett,2007,56:223-229
[5] Golec J,Sathananthan S.Sample Path Approximation for Stochastic Integro-differential Equations[J].Stoch Anal Appl,1999(17):579-588
[6] Golec J,Sathananthan S.Strong Approximation of Stochastic Integro-differential Equations[J].Dyn Contin Discrete Impuls Syst Ser B Appl Algorithms,2001(8):139-151
[7] Mao X.Exponential Stability of Stochastic Differential Equations Marces Dekker[M].New York:[s.n.],1994
[8] Mao X.Stability of Tochastic Integro-differential Equations[J].Stoch Anal Appl,2000,18:1005-1007
[9] Rathinasamy A,Balachandran K.Mean-square Stability of Milstein Methods for Liner Hybrid Stochastic Delay Integro-differential Equations[J].Nonlinear Anal.Hybrid Syst,2008(2):1256-1263
[10] Rongcheng Yin,Fuke Wu,Shigeng Hu.A Class of Stochastic Differential Equations with the Time Average[J].Acta Math Sin English Series,2014(30):525-538
[11] G Da Prato,J Zabczyk.Stochastic Equations in Infinite Dimensions[M].UK:Cambridge University Press,1992
