离散多智能体系统的分布式编队跟踪控制

林 涛，韩娜妮，刘仰魁



离散多智能体系统的分布式编队跟踪控制

*林 涛，韩娜妮，刘仰魁

（陇东学院电气工程学院，甘肃，庆阳 745000）

本文研究了离散多智能体系统在固定有向拓扑中的分布式编队控制，同时假设此系统跟踪时变参考状态。首先，针对一阶系统设计了控制协议，给出了系统稳定时协议参数需满足的充要条件，结果表明，跟踪误差的上限正比于采样周期。其次，针对二阶系统，考虑了速度一致性，其编队控制协议可用同样的方法研究。最后通过仿真，结果证明了所设计协议的有效性。

多智能体系统；分布式编队控制；一致性协议；离散；参考智能体

分布式编队控制作为多智能体协作控制的一个重要方面，在实际生活中有着极为广泛应用，并且得到许多研究成果。文献[1]~文献[5]对智能体系统都做了深入研究，但都是针对连续的多智能体系统，实际中的系统大都是离散系统。相对于集中式控制策略，分布式控制策略可靠性高并且简单。本文在现有文献的基础上，研究了离散多智能体系统在固定拓扑中的leader-following编队控制问题，并且假设多智能体跟踪时变参考状态。在所设计的协议作用下，二阶多智能体系统所要求的编队同时能够保持速度一致性，且能以固定误差跟踪时变参考状态。仿真结果表明我们设计的协议有效，所得出的结论对实际中的多智能体系统的编队跟踪控制问题具有一定的应用价值。

1 系统描述

我们考虑一个由个follower agents和一个leader agent组成的网络，leader agent标注为+1。这时，这个智能体网络就可以用一个加权有向图来描述。

设个followers智能体一阶和二阶动态方程分别为：

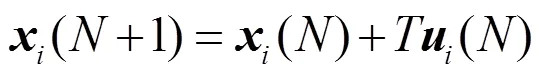
和

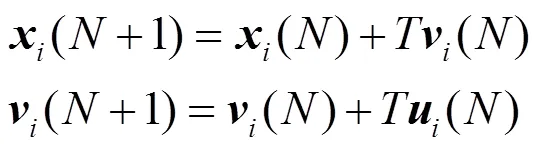
已有的关于智能体编队控制的研究成果基本都是基于以上的两个模型。其中的二阶模型中，我们加入了速度一致项，使得模型更加完善，更贴近实际情况。

设Leader智能体对应的模型为：

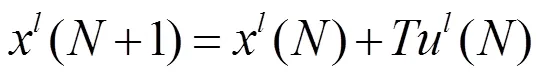
和

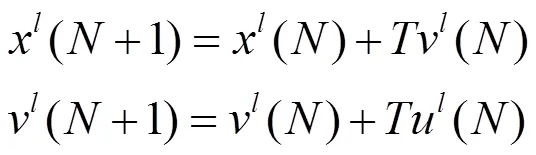
2 基于一阶、二阶模型的编队控制

2.1 基于一阶模型的编队控制

针对系统(1)，设计如下控制协议

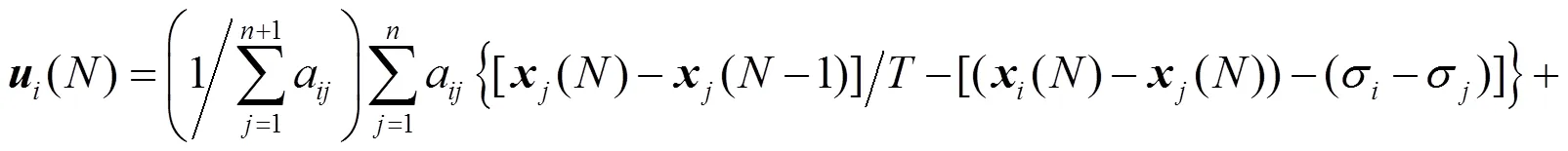
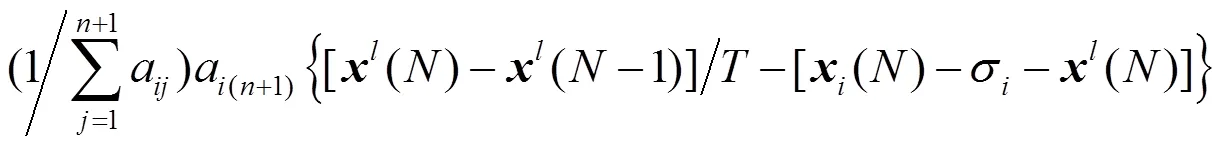
则协议(5)可写为：

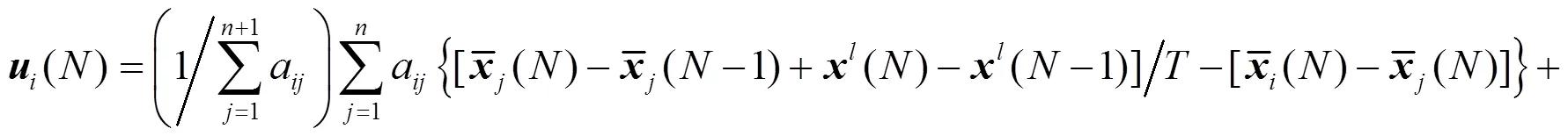
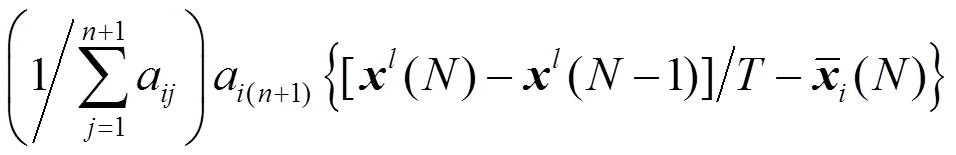
联立式(1)，(3)，(6)和(7)式，可得到下面的跟踪误差方程：

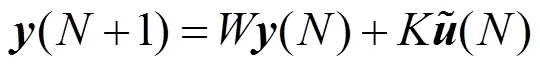
式中，

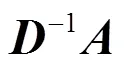
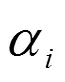
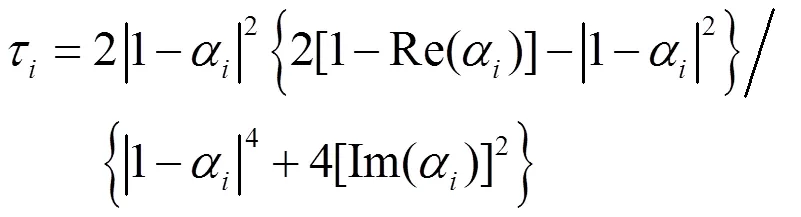
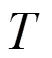
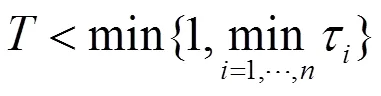
则的所有特征值都在单位圆内。

证明：由引理1和引理2，可得误差系统(9)稳定。并从式(9)可得到

上式中用到

由文献[5]，可直接得到

引理1与引理2的具体证明见文献[6]。基于文献[6]，本文研究了一阶离散多智能体系统分布式编队跟踪控制，并在一致性研究基础上加入相对位置的信息，使其更加符合实际环境的需求。

2.2 基于二阶模型的编队控制

针对系统(2)，我们设计如下控制协议：

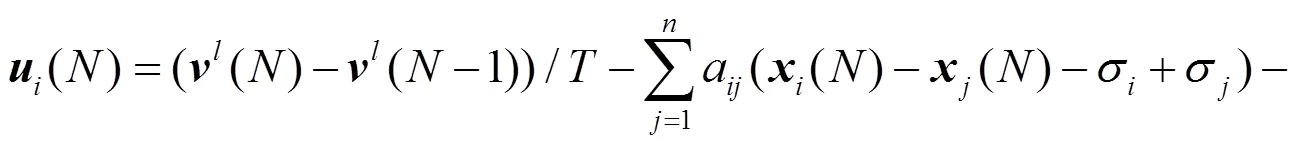
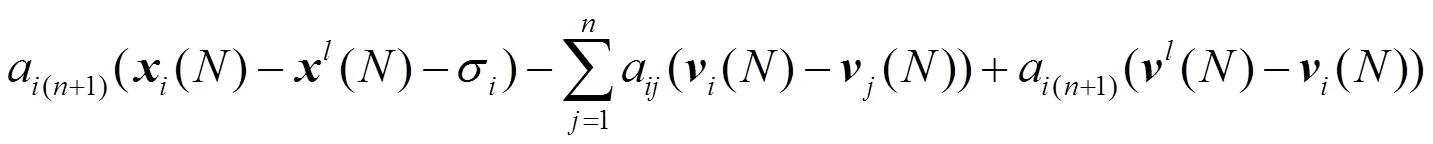
则协议(3)可以写为

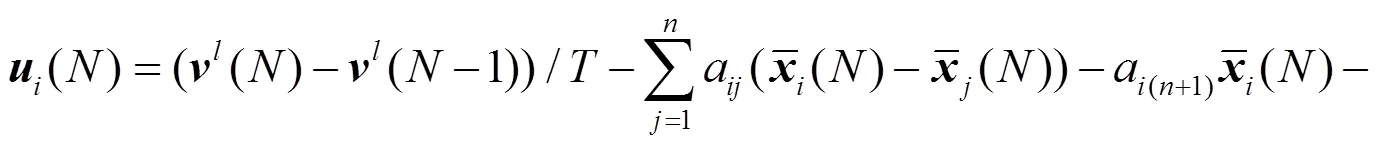
联立 (2)，(4)，(12)和(13) 式，可得到如下误差动态系统方程：

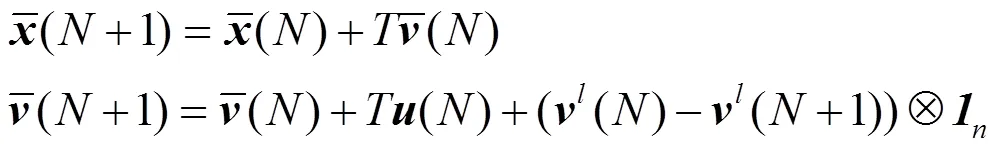
将(13) 式代入(14) 式，可得

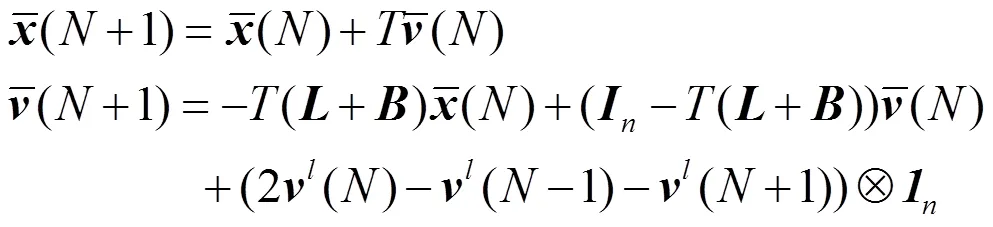
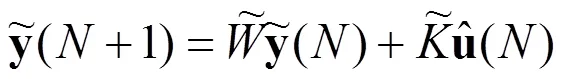
式中

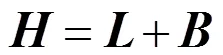
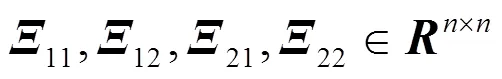
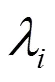
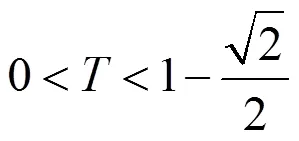
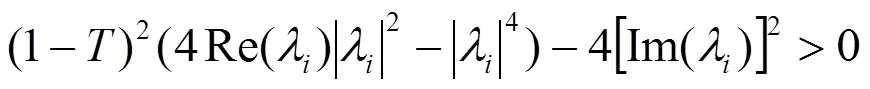
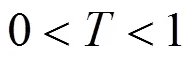
则矩阵的所有特征根都在单位圆内。

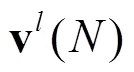
证明：由引理5，可知误差系统(16)稳定，且从 (16)式可得

网络的拓扑结构对系统的性能有着重要的影响，定理１、定理2给出了当网络拓扑在满足给定条件时，若对采样周期加以限制，则所设计的协议就能达到控制目标。

3　仿真研究

3.1　一阶系统的仿真及结果分析

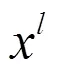
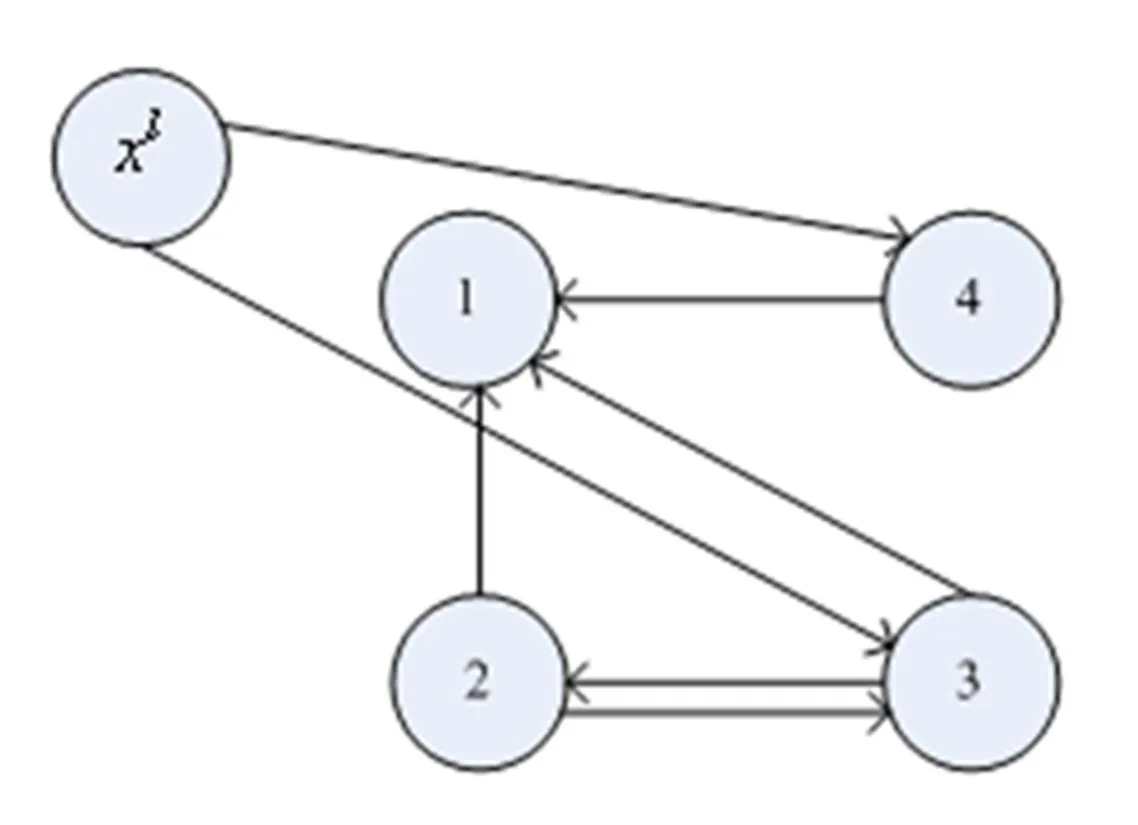
图1　多智能体网络拓扑结构

Fig. 1 The interaction topology of multi-agent systems network

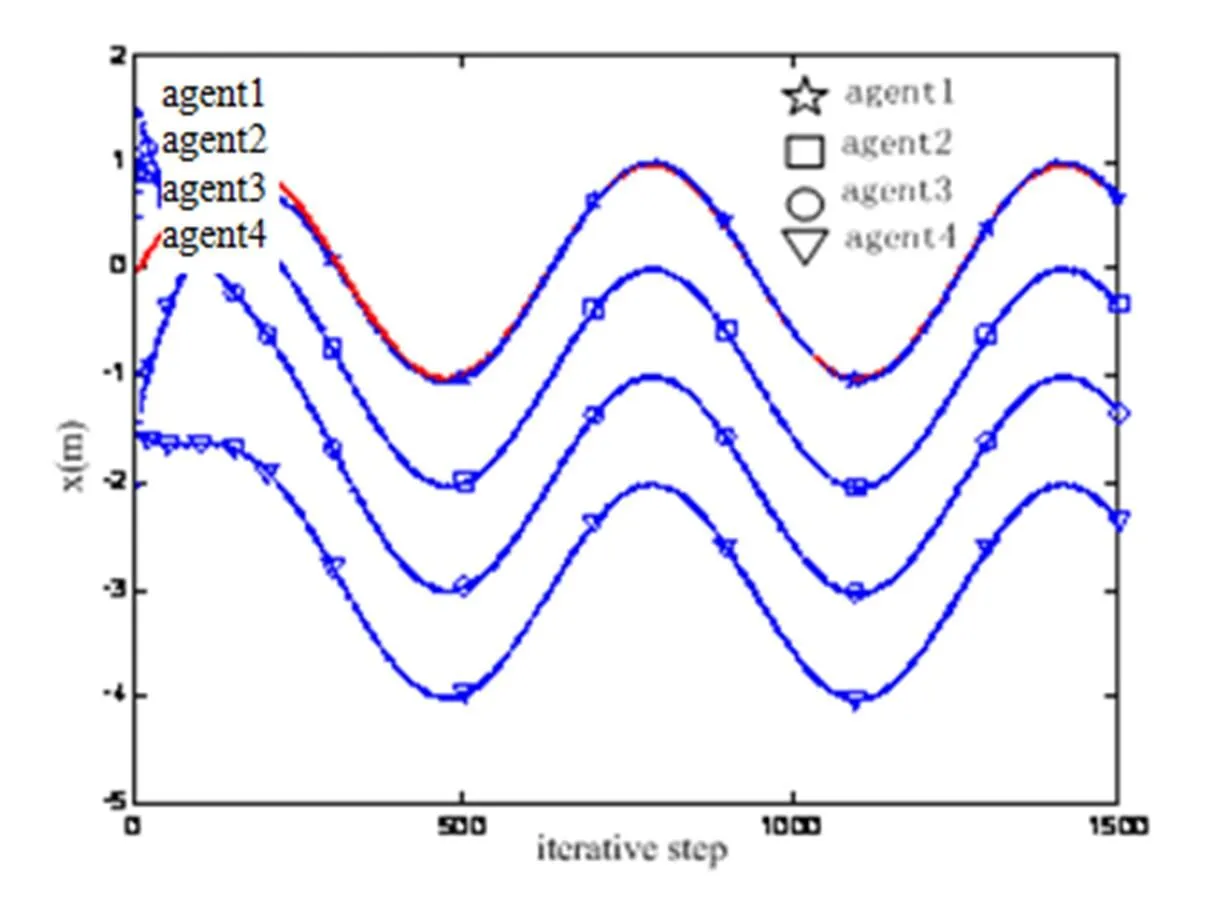
图2　时系统(1)的位置轨迹

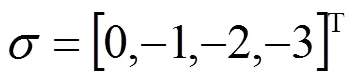
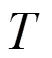
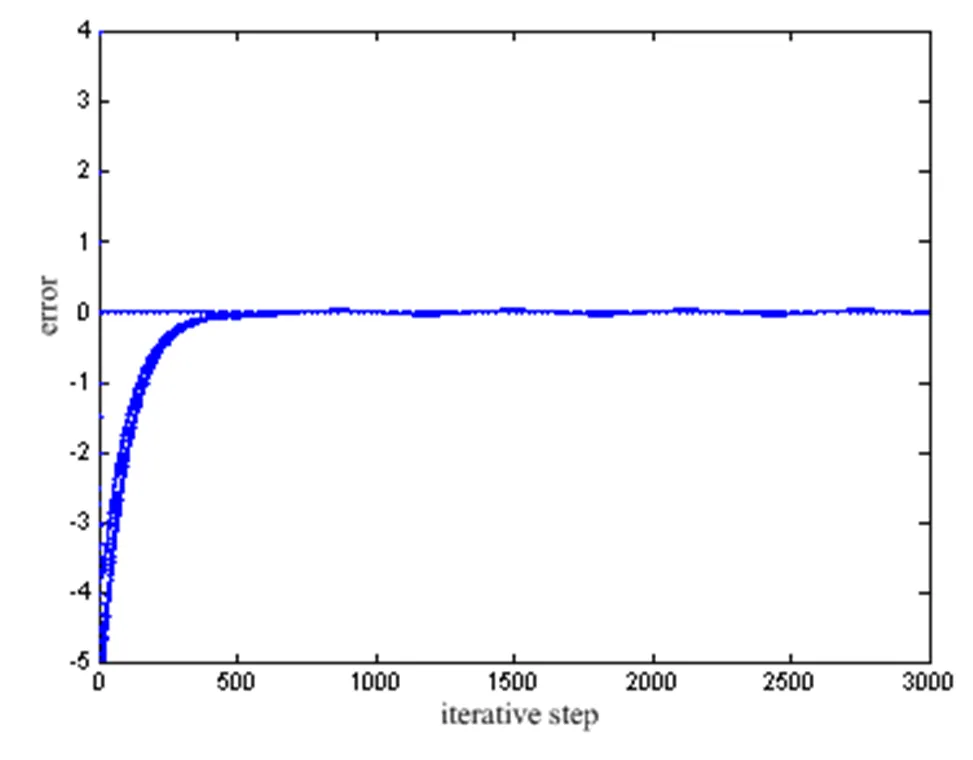
图3 T=0.01s时误差系统(9)的状态轨迹

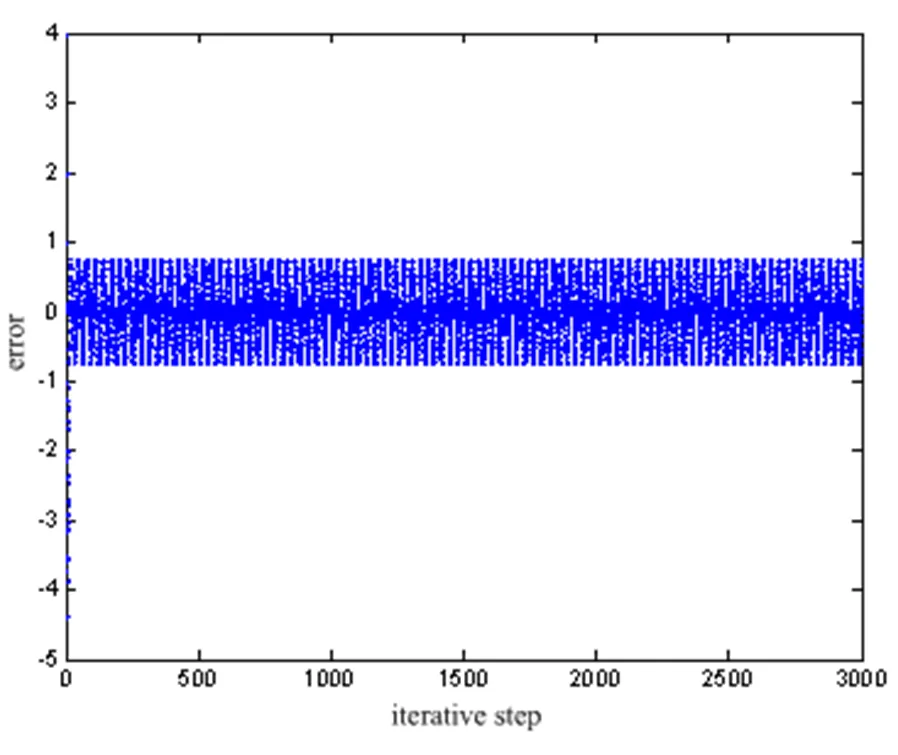
图4 T=0.2s时误差系统(9)的状态轨迹

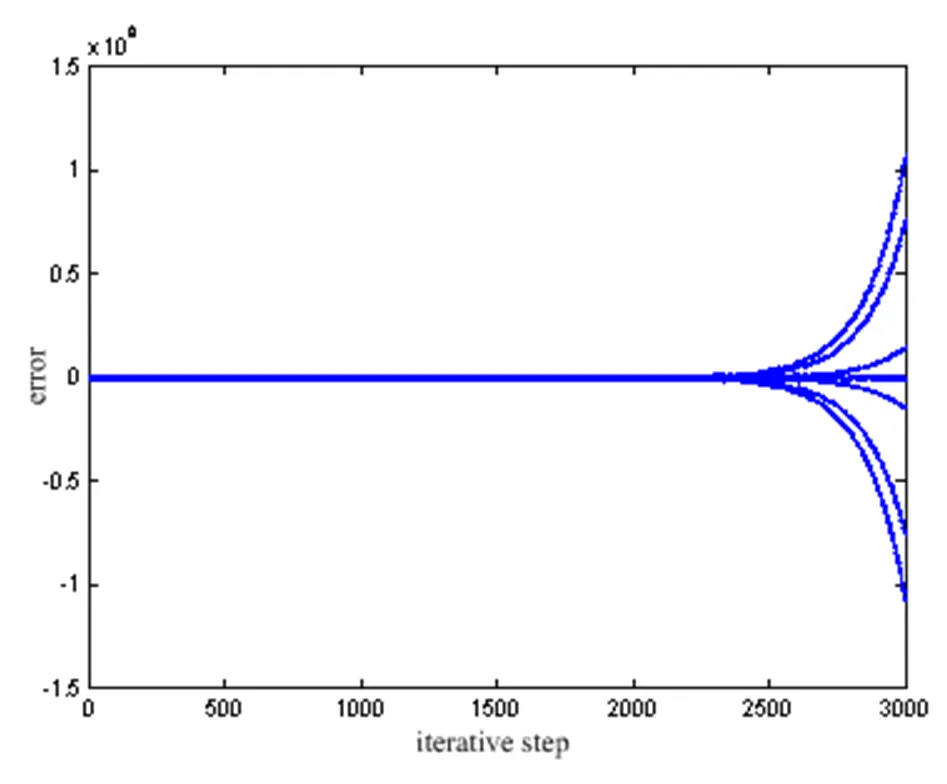
图5 T=0.35s时误差系统(9)的状态轨迹

3.2 二阶系统的仿真及结果

考虑一个leader和4个followers智能体所构成的网络，其拓扑结构如图6所示，由图可知从leader到任一followers都有一条有向路径。

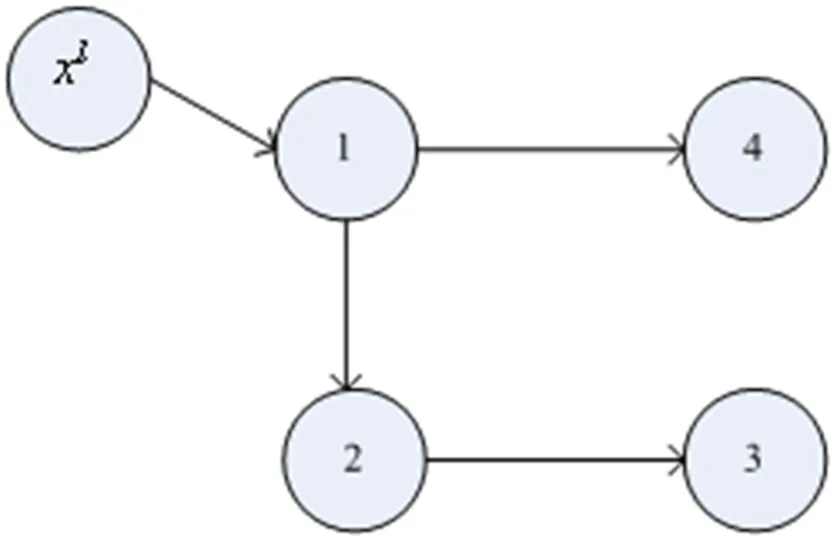
图6　多智能体网络拓扑图

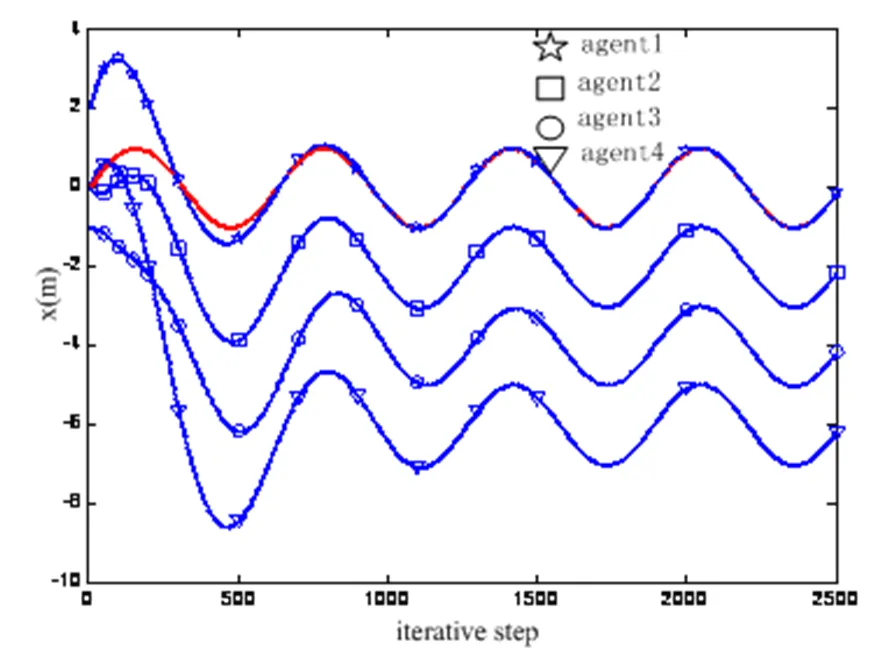
图7　时系统(2)的位置轨迹

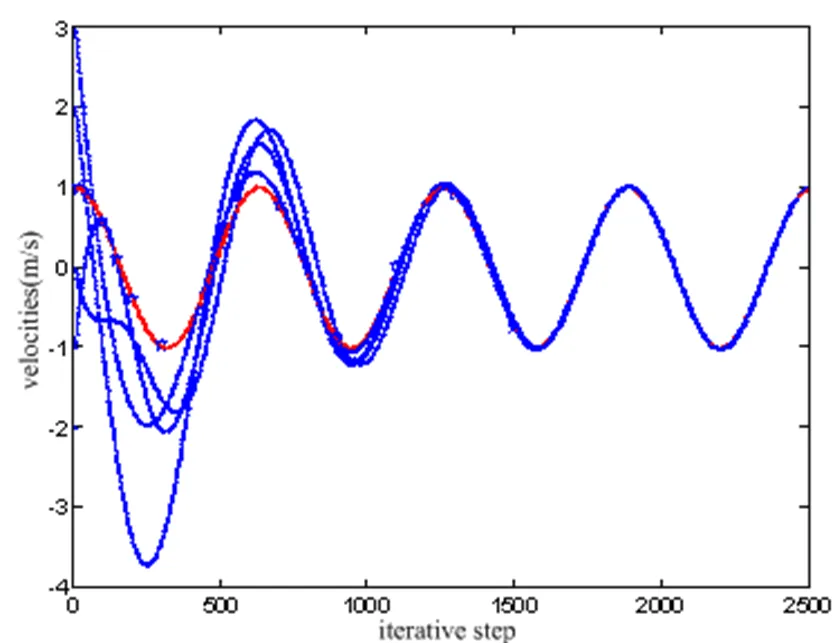
图8　时系统(2)的速度轨迹

图8为系统(2)的速度轨迹。由图可以看出，4个followers的速度逐渐趋于一致，leader的速度曲线用加星号线来表示，且4个followers智能体始终保持预期的编队。

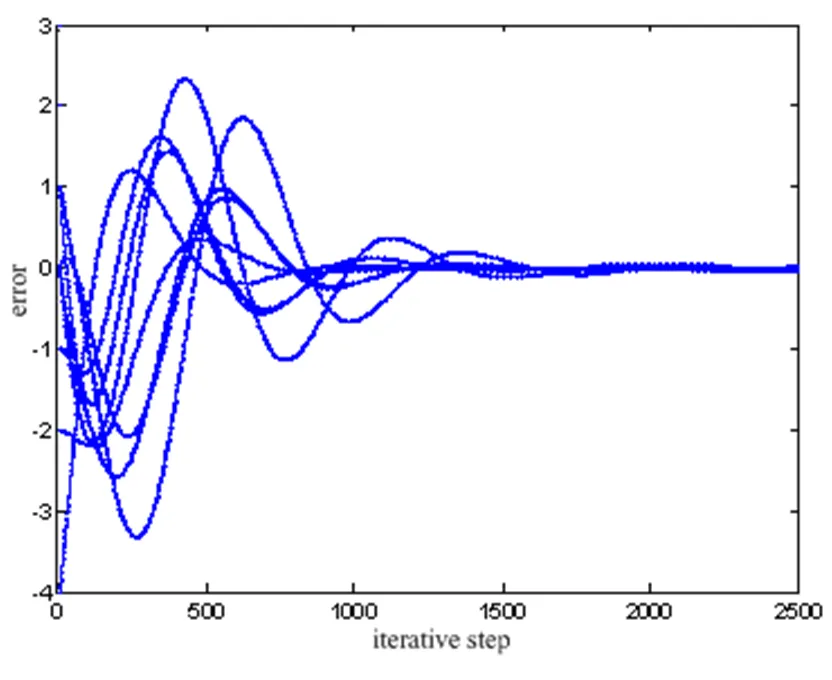
图9　T=0.01s时系统(16)的误差状态轨迹

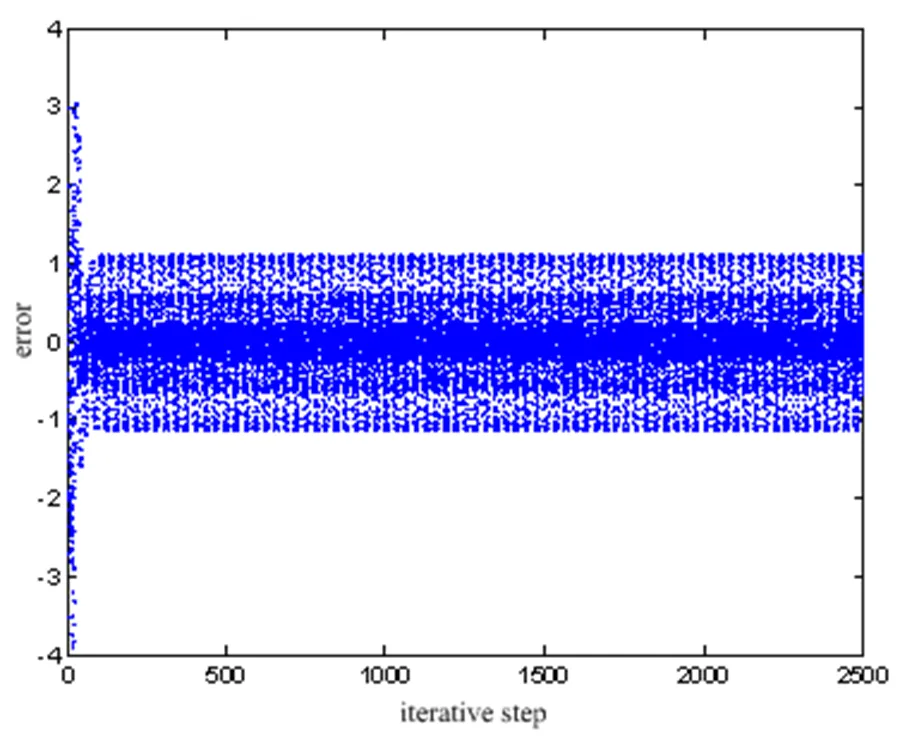
图10　T=0.2s时系统(16)的误差状态轨迹

图9和图10为采样周期分别为0.01s、0.2s时系统(８)的误差状态轨迹。从图可知，跟踪误差与采样周期成正比。

4 结束语

在实际生活中离散系统的应用极为广泛，所以对离散系统编队跟踪问题的研究有着重要的现实意义。本文针对一阶和二阶离散多智能体系统，设计出编队控制的协议，使followers智能体能组成期望的编队，并迅速跟踪leader 运行轨迹。给出了所设计的协议有效时采样周期必须满足的充要条件，并且指出跟踪误差正比与采样周期。仿真结果表明，所设计的协议有效、对现实生活的智能体控制问题具有重要的意义。

[1] Liang Y, Lee H H. Decentralized formation control and obstacle avoidance for multiplerobots with nonholonomic constraints[C]. Proceedings of the 2006 American Control Conference, 2006: 5596-5601.

[2] Bazoula A, Djouadi M S, Maaref H. Formation Control of Multi-Robots via Fuzzy Logic Technique [C]. Proceedings of ICCCC, 2008:179-184.

[3] Hou Z G, Cheng L, Tan M. Decentralized Robust Adaptive Control for the Multiagent System Consensus Problem Using Neural Networks[J]. IEEE transactions on systems, 2009(39): 636-647.

[4] Ren W. Multi-vehicle consensus with a time-varying reference state. Systems and control letters, 2007:474-483.

[5] Cao Y C, Ren W, Yan L. Distributed discrete-time coordinated tracking with a time-varying reference state and limited communication[J]. Automatica, 2009(45): 1299-1305.

[6] Gu D B, Hu H S. Distributed network-based formation control[J].International Journal of Systems Science, 2009(40): 539-552.

[7] Cao Y C, Ren W, Li Y. Distributed Discrete-time Coordinated Tracking with A Time-varying Reference State and Limited Communication[J]. Automatica, 2009, 45(5):1299-1305.

The Distributed Formation Tracking Control of the Discrete Multi-agent System

*LIN Tao，HAN Na-ni，LIU Yang-kui

(Electrical Engineering College, Longdong University, Qingyang, Gansu 745000,China)

We investigate the distributed formation for discrete-time multi-agent systems with a time-varying reference state in fixed directed communication topology. The multi-agent systems modeled as first-order and second-order equations are both considered. Firstly, the protocol for the first-order system is proposed, under which the agents can be able to track the time-varying reference state while maintaining the desired formation. We give a sufficient and necessary condition that the sampling period satisfies to ensure the stability. Furthermore, we study the quantitative bound of the tracking error. It is shown that the ultimate bound of the tracking error is proportional to the sampling period. The multi-agent system described as second-order equations is developed by using the same way and the velocity consensus is concerned as well. Finally, the simulation results illustrate the effectiveness of the designed protocols.

multi-agents systems; distributed formation control; consensus protocol; discrete-time; reference agent

1674-8085(2014)01-0060-06

TP273

A

10.3969/j.issn.1674-8085.2014.01.013

2013-06-25；

2013-10-12

陇东学院青年科技创新项目(XYZK1009)

*林 涛(1978-)，男，甘肃庆阳人，讲师，硕士，主要从事智能控制理论及应用研究(E-mail:lintao8888231@sohu.com);

韩娜妮(1986-)，女，甘肃庆阳人，讲师，硕士，主要从事多智能体系统的分布式编队控制研究(E-mail：253182145@qq.com);

刘仰魁(1953-)，男，甘肃庆阳人，教授，主要从事电力电子技术研究(E-mail:gs-lyk@163.com).