BP神经网络模型预测高速铁路路基沉降的适用性分析

王杜江

(中铁第一勘察设计院地路处，陕西西安710043)

人工神经网络通过模拟人的大脑神经处理信息的方式实现信息并行处理和非线性转换，具有很好的自学习能力。Back Propagation(BP)网络是目前应用频率最高的神经网络，体现了神经网络中最精华、最完美的内容［1］。地基沉降受多种因素的影响，其变化的规律很难用一个数学显式来表示。人工神经网络视传统的函数自变量和因变量为输入和输出，将传统的函数关系式转化为高维的非线性映射，可以将影响地基沉降的众多因素用数学显式来表达，在处理非线性问题上具有独特的优越性。而对于高速铁路路基沉降量级小、数据波动大的特点，其适用性也有待探索和研究。本文以武广高速铁路乐昌段19个路基断面的沉降数据为研究对象，利用Matlab软件建立BP神经网络预测模型，计算原始模型和改进模型的预测误差，对两种模型的适用性进行评价。

1 传统BP网络模型的适用性

1.1 基于Matlab的BP神经网络模型建立

1.1.1 输入输出参数的确定

影响路基沉降的因素很多，对这些因素的考虑决定了预测的精度。确定影响因素时应该抓主要因素，精简次要因素。根据工程经验，影响路基沉降的主要因素有地基参数(软土厚度、土层压缩模量等)、路堤填土参数(填土高度、密实度等)、地基处理方式、时间因素(填筑工期、静置时间)。根据武广客运专线DK1943～DK1945段路基的实际工况及工程特点，本文选择软土厚度、地基处理方式、地基土压缩模量、路堤填土高度、施工工期、铺轨前沉降量六个参数作为模型的输入，输出数据位路基的最终沉降量。

1.1.2 模型结构

经过分析研究和大量试算，确定BP神经网络模型为3层结构:

(1)输入层元素个数为输入参数的个数，即n=6。(2)输出层元素个数为输出参数的个数，即m=1。

(3)隐含层节点数以经验为依据，结合实例数据进行试算确定。一般有两种经验公式用于确定隐含层的神经元个数，如式(1)和式(2):

或

式中:n1为隐含层神经元个数;n为输入层神经元个数;m为输出层神经元个数;a为1～10之间的常数。

BP神经网络结构图见图1。

图1 BP神经网络结构图

1.1.3 网络训练及检验

由于BP网络输入点物理量各不相同，数值相差较大，在计算过程中可能出现“大数吃小数”的情况，而且当网络输入和目标矢量的取值在［－1，1］时，trainbr函数可以达到最好的工作效果。为了加快网络收敛速度，在使用样本数据前，对数据要进行归一化处理。为了克服经典BP算法收敛速度慢、易遇到局部极小点而难于收敛等缺点，本文采用自适应学习速率的动量BP改进算法。通过设定训练次数和训练误差来控制训练效果，当训练次数超过设定值或训练误差小于设定值时，网络自动停止训练。网络训练完成后，就可以训练样本进行预测。BP网络参数见表1，网络预测模型图见图2。

图2 神经网络预测模型

表1 BP网络的参数

1.2 BP神经网络模型的预测效果

采用以上建立的BP神经网络模型对19个断面的沉降进行预测，预测方法:将每个断面恒载期的沉降数据作为训练样本，预留最后三个数据为校验数据，计算所建模型的相关系数和相对误差。结果如表2所示:

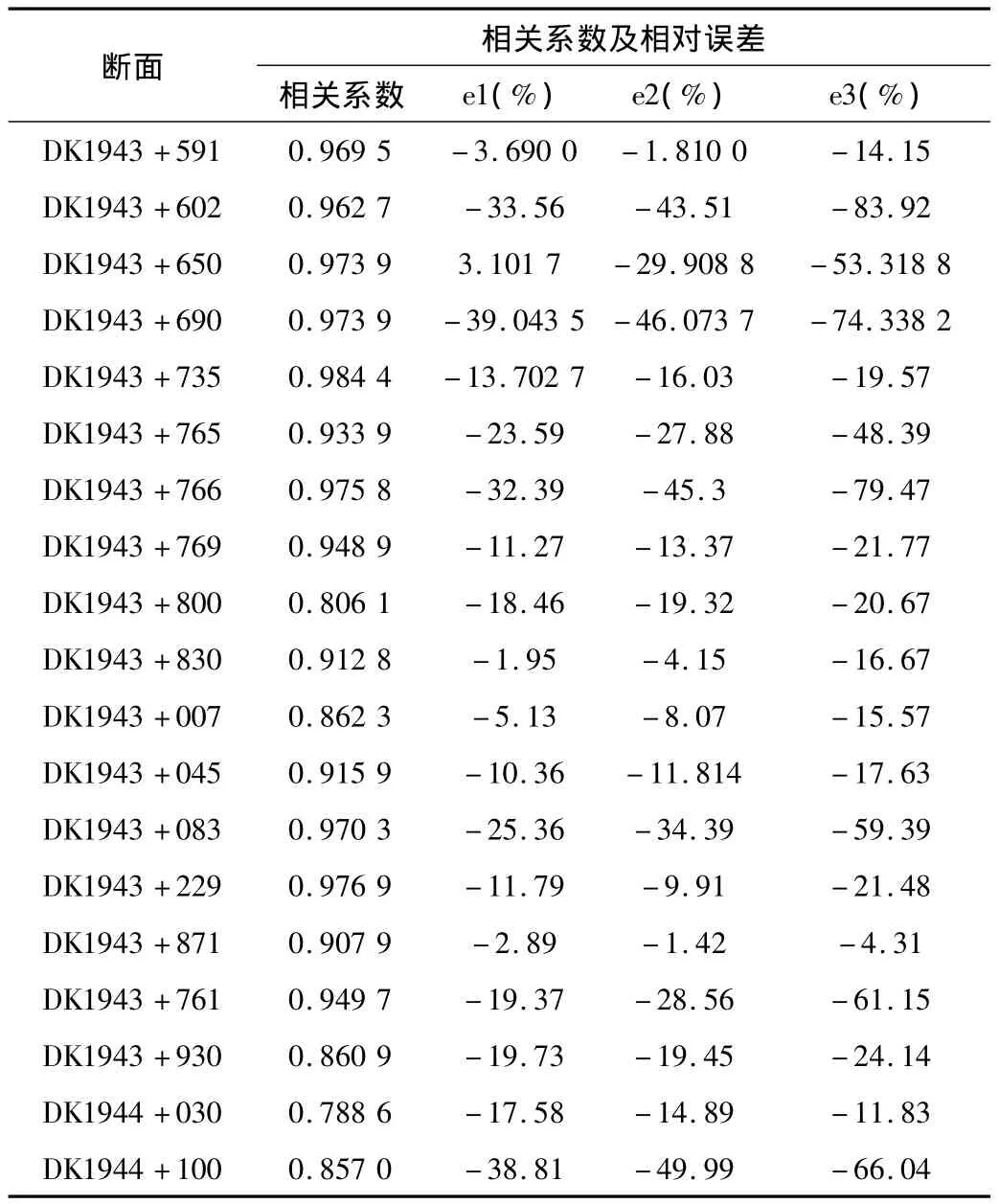
表2 BP神经网络预测效果

由以上结果可知:BP神经网络模型的预测误差大，不满足《客运专线无砟轨道铺设条件评估技术指南》对预测模型“相关系数不小于0.92，预测误差在5%以内”的要求。高速铁路的实测数据波动大、沉降量级小，受影响因素多，可见将BP神经网络直接应用于路基沉降预测并不适用，需要对其模型结构及算法进行改进。

2 模型的改进及其预测效果

BP神经网络的是基于梯度法原理的误差逆传播模型，其收敛速度慢、容易产生局部最优等缺点难以避免。对BP网络的工程应用中，一般都根据经验来选择的网络结构，如隐含层大都选为1层，隐含节点数也由经验公式确定。但对于隐含层与隐含节点的最优匹配关系、输入输出节点数目与隐含层数的匹配关系还不明确，有待做优化尝试。本文将从算法和结构两个方面对BP神经网络进行改进，并采用后验差对拟合结果进行检验。

2.1 隐含层数及隐含节点数的优化

研究表明，BP神经网络的隐含层数一般取1就可以满足需要，最多取2;隐含层的节点数太多或太少都不利于网络的学习，根据文献［2］的研究成果，隐含层的节点数在4～9之间比较合适［2］。现利用前面19个断面的沉降监测数据，分别建立隐含层个数为1和2的网络模型，利用Matlab编程计算，并对网络的训练效果进行对比，结果见表3。

表3 不同隐含层数网络训练效果对比

由训练结果可知，隐含层数为2的BP网络能在较少的训练次数内达到更高的精度，训练效果明显优于隐含层数为1的网络模型。

2.2 GA－BP模型的建立

遗传算法(genetic algorithm，GA)力求充分模仿生物自然进化过程的随机性全局性的特点，是一种具有高度并行和自适应搜索能力的计算方法，具有强大的全局寻优能力［3－6］。用GA算法对BP网络的初始权值进行优化，可以实现两种算法的优势互补。用GA算法改进BP神经网络的步骤如下:

(1)建立GA－BP神经网络模型，并初始化:

(2)建立染色体和初始种群:

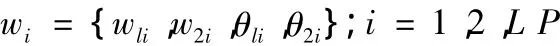
式中:wi为审计网络的权值，每个完整的权值相当于一个染色体;wli为隐含层的权值;w2i为输出层的权值;θli为隐含层的阈值;θ2i为输出层的阈值;P为种群规模。

(3)遗传算法参数的确定:

遗传算法的参数主要有3个，即种群规模P0、杂交率Pc和变异率Pm。种群规模直接决定着遗传算法的最终效果，如果种群规模过大，则网络收敛速度过慢;如果种群规模过小，则容易使算法陷入局部最优解。杂交率控制着杂交算子的应用频率，对于特定的种群规模，存在着最优杂交率，而且最优杂交率有随着种群规模的增大而降低的规律。变异率是为了使网络在训练过程中实现“优胜劣汰”而设置的变异基因比例，一般高于0.05变异率会使遗传算法的在线性能下降。

综合遗传算法的原理和特点，参考以往经验［7］，在本算例中各参数的取值如表4所示:

表4 GA算法参数

(4)算法的实现:

先用GA算法优化权值，再利用BP算法迭代优化权值。参考文献［8］中的经验［8］，设置混合算法中的最大代数K=500，精度ε=0.005，BP算法中最大代数E=1 000，采用Matlab编程，隐含层的激励函数采用S型函数。算法流程如下图所示:

图3 GA－BP算法流程图

2.3 GA－BP模型的预测效果

利用训练好的GA－BP网络模型对前述19个断面的沉降进行预测，并与单纯的BP神经网络拟合效果进行对比，结果如图4、图5所示:

图4 相关系数与相对误差分布图

图5 GA－BP模型拟合曲线图

由以上对比结果可知，和单纯的BP模型相比，采用双隐含层的网络结构的GA－BP网络模型可以明显减小误差，除个别断面由于数据波动太大导致最后的拟合效果不理想外，大部分断面的拟合相对误差在5%以内，而相关系数在0.92以上，多数断面的相关系数达到了0.98，满足高速铁路路基沉降变形评估的要求。说明遗传算法可以有效改善BP网络容易陷入局部最小的缺陷，可提高模型的预测精度和稳定性。

3 结语

对于高速铁路路基沉降量级小、数据波动大的特点，传统的BP神经网络模型适用性较差，从结构和算法两方面对模型改进后预测效果明显改善。从本文的分析结果看，采用双隐含层的GA－BP网络模型的预测精度较高、预测稳定性较好，可以作为高速铁路路基工后沉降预测及评估的有效方法。该模型的缺陷是，在长期预测中稳定性欠佳。

［1］A C A A E.Boron phosphide(BP)bulk modulus［J］.2001.

［2］杨茜.BP神经网络预测方法的改进及其在隧道长期沉降预测中的应用［J］.北京工业大学学报.2011(1):92－97.

［3］玄光男，程润伟.遗传算法与工程设计［M］.北京:科学出版社，2000.

［4］张建雄，唐万生.基于混沌遗传算法的一类非线性两层混合整数规划问题求解［J］.系统工程理论方法应用，2005，14(5):429－433.

［5］Shrestha R，Rode M.Multi－objective calibration and fuzzy preference selection of a distributed hydrologicalmodel［J］.EnvironmentalModelling and Software，2008，23(12):1394 －1395.

［6］Murase M，Ono K，Ito T，et al.Time－dependentmodel for volume changes in pressure sources at Asama volcano，central Japan due to vertical deformations detected by precise leveling during

［7］李红霞，赵新华，迟海燕，等.基于改进BP神经网络模型的地面沉降预测及分析［J］.天津大学学报.2009(1):60－64.

［8］林德，米合华，丁文其，等.岩土工程问题安全性的预报与控制［M］.北京:科学出版社，2009.

［9］付宏渊.高速公路路基沉降预测及施工控制［M］.北京:人民交通出版社，2007.