解析法和数值法在丘陵地区矿坑涌水量预测中的比较

2014-03-15彭洪涛朱常春陶月赞

地下水 2014年3期

彭洪涛，王昊，朱常春，陶月赞

(合肥工业大学土木与水利工程学院，安徽合肥230009)

矿坑涌水量的大小在一定程度上受矿床水文地质条件的影响，也是矿山开采设计中制定防、治水方案的依据。多年来，很多学者从不同角度、利用不同方法做了大量的工作。水文地质比拟法、涌水量曲线方程法、解析法、集水廊道法、水均衡法和数值法等为现在国内外常用的预测方法［1］。每种方法都有其特点，同时也有所局限。因此，本文在充分分析矿坑充水条件、合理选用计算参数、详尽查明矿坑充水因素的基础上，采用解析法和数值法两种方法对研究区的矿坑涌水量进行预测。

矿区地处丘陵地带，第四系松散层盖与基岩风化壳都比较薄，土壤保水与保墒能力本身就比较脆弱，这类地区天然地下水流系统一旦受到破坏，首先将对农村零星饮用水和农业灌溉形成直接影响，如处理不慎，往往导致当地群众与矿山企业之间关系紧张;但如上所述，国内外关于矿山开采对地下水资源影响方面的研究，多偏重于平原地区，少有关注丘陵地带的相关研究［2］。因此，本文庐江丘陵地区某铁矿为例，分别采用解析法和数值法对研究区的矿坑涌水量进行预测，并将两种方法的预测结果进行了对比分析。

1 研究区概况

研究区位于庐江县城东南方向约26 km处，地处江淮丘陵南部，属丘陵区地形，海拔标高一般在+20～+60 m。研究区属亚热带湿润季风气候，气候温和，雨量充沛，四季分明。年平均降雨量为1 248.2 mm，年平均蒸发量为1 402.3 mm。

研究区地层按含水介质类型划分为四个含水岩组。1、松散岩类孔隙含水岩组:水量贫乏—中等的，单井涌水量10～1 000 m3/d;2、火山碎屑岩孔洞裂隙含水岩组:钻孔单位涌水量0.149 5 ～2.04 L/s·m，渗透系数0.23 ～1.30 m/d;3、碎屑岩、碳酸盐岩类岩溶—裂隙含水岩组:水位埋深9.50～16.42 m，钻孔单位涌水量0.031 1 ～0.318 4 L/s·m，渗透系数0.07 ～0.36 m/d;4、熔岩、次火山岩、粉砂岩、矿体裂隙含水岩组:风化带以下岩层含水性差，单位涌水量0.000 01 L/s·m，渗透系数为0.001 2 m/d左右。

研究区无大型地表水体，区内大气降水是地下水的主要补给来源。浅部风化裂隙潜水，降水入渗后，经渗流，呈下降泉出露，深部的地下水，接受复杂的裂隙系统的入渗补给，由补给区缓慢地向排泄区运移。天然状态下矿床地下水均向沟谷中就近排泄，排泄方式主要有三种:蒸发排泄，泉水排泄和开采排泄。

2 充水因素分析

矿床地形有利于自然排水，地表水体不发育，一些暂时性的沟谷溪流并不构成对矿坑的威胁。矿体顶底板直接充水的裂隙含水岩层多出露地表，降水入渗补给是矿坑充水的唯一水源。北部富水性中等的碳酸盐岩岩溶裂隙含水层局部地段与矿体接触，形成矿坑侧向充水来源。另外，矿床范围内各含水岩组有一定的差异，其间无明显的连续稳定隔水层存在，天然状态下各含水岩组间有一定的水力联系，总体是降水通过风化裂隙由浅部向深部补给。地下水位总体随地形变化，不同含水岩组分布区水位呈渐变关系，无明显水位跌落，反映出各含水岩组间具有统一的水动力场。断裂构造对不同含水岩组间水力联系起沟通作用。

3 矿坑涌水量预测

3.1 解析法预测

考虑该矿区充水边界条件，矿坑涌水量计算采用稳定流完整井的“大井法”估算，计算公式如下:［3］

式中:Q为预测的矿坑涌水量(m3/d);K为渗透系数(m/d);H为承压含水层从底板起算的水头值(m);M为承压含水层厚度(m);h为从底板起算的井内或矿坑内的水位高度值(m);S为水位降深(m);R0为矿井采区引用影响半径(m);r0为矿井采区引用半径(m);R为单井影响半径(m);F为预计矿井开采面积(m2);b1为采区中心至西部隔水边界的距离(m);b2为采区中心至北部隔水边界的距离(m)。

渗透系数(K):根据已收集的抽水试验资料，以试段长度为权重、加权平均取得整个承压含水层的渗透系数(见表1)。

表1 承压含水层渗透系数表

含水层厚度(M)与水头值(H):综合考虑裂隙发育程度、冲洗液消耗和水位变化情况，承压水含水层厚度取平均327.56 m。水位高程则取ZK122孔两个试段水位高程的均值(见表2)。

表2 承压含水层厚度(M)与水头值(H)

矿井采区引用半径r0与采区引用影响半径R0:根据矿体水平投影图量测，本矿床矿体面积426 988.58m2;未来矿山排水疏干、降深达到最大值时，动水位最终会降到承压含水层底板，因而矿坑内的动水位高度为零。按公式可以计算得到引用半径r0与引用影响半径R0(见表3)。

表3 矿井采区引用半径r0与引用影响半径R0

采区中心至西部、北部边界(b1、b2)距离:将两方向的隔水边界概化成直线隔水边界，从平面图量得本矿床采区中心距:西部边界b1为850 m，北部边界b2为1 120 m。计算结果见表4。

表4 矿坑涌水量估算采用参数与结果表(解析法)

3.2 数值法预测

3.2.1 水文地质概念模型

根据区域水文地质资料，研究区从上到下概化为4个含水岩组，松散岩类孔隙含水岩组、火山碎屑岩孔洞裂隙含水岩组、碳酸盐岩岩溶裂隙含水岩组和熔岩、次火山岩、粉砂岩、矿体裂隙含水岩组。并综合考虑岩性及裂隙发育程度，将模拟区地层概化为六层，自上而下分别代表含砾粘土层、粗安岩、粗安斑岩、粉砂岩、矿体裂隙含水岩组及矿床底板。

研究区天然状态下，地下水由南向北流动，河流流向与地下水等水位线垂直，东西两侧概化为零流量边界;北部以西河为边界，为排泄边界，由于研究区内地下水疏干排泄及水井开采对边界水位几乎无影响，可概化为定水头边界;南部为海拔较高丘陵，概化为隔水边界;模型上边界主要接受大气降水补给及潜水蒸发排泄，故概化为为降水入渗补给、蒸发边界;矿床深部为岩石富水性极弱，可概化为隔水层。

3.2.2 数学模型

根据水文地质概念模型及含水岩组的水力性质，将模拟区地下水流概化成非均质各向异性非稳定准三维地下水流系统，并建立相应的数学模型。［4］［5］

式中:Kx、Ky、Kz为渗透系数在 x、y、z方向的分量(m/d)，(假定渗透系数主轴方向与坐标轴的方向一致);h为地下水水位(m);W为单位体积流量，用以代表流进源或流出汇的水量;μs为含水岩组的储水率(1/m);h0(x，y，z)为已知水位分布(m);t为时间(d);D为模拟区范围;Γ1为一类边界;Γ2为二类边界;q(x，y，z，t)为二类边界上的已知流量分布。

3.2.3 模型识别

水位拟合:研究区可作为水位过程识别的长期动态观测资料较少，仅有ZK1915长期观测孔1983年3月－1986年12月和ZK45长期观测孔2011年2月－7月的逐月水位观测数据，因此利用以上两个长观孔观测资料对模型识别的结果进行识别。识别结果见图1。

图1 基岩含水岩组水位动态拟合过程线

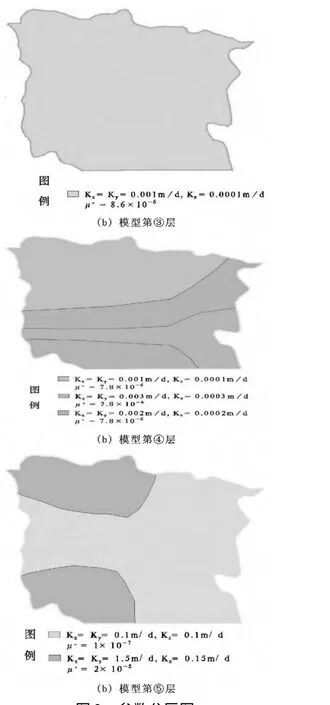
图2 参数分区图

参数识别:依据矿区水文地质条件，对参数进行分区。经过模型识别后得到区内各层参数分区及取值情况，如图2所示。图中不同分区的参数取值可基本反映模拟区的水文地质条件。

3.2.4 预测结果分析

经识别后的模型，预测得到－500 m开采水平的涌水量随时间的变化过程如图3所示，初期涌水量为10 309m3/d，随着矿床开采的进行，矿坑涌水量逐渐减小，开采5年后涌水量约减小为3 788 m3/d，此后，递减幅度逐渐减小，水量趋于平稳，约为3 150 m3/d。涌水量在趋于平衡过程中，有一定的起伏变化，主要原因是受汛期和枯水期大气降水量不同影响。