三相流化床流动结构特征的小波分析

贺婷婷 钟文琪 李蔚玲 金保昇

(东南大学能源热转换及其过程测控教育部重点实验室，南京210096)

气液固三相流化床在石油化工、生物工程、医药科学等领域有着广泛的应用，如煤液化[1]、费托合成[2]、废水处理[3]等.与气固、气液流态化相比，气液固三相流态化具有自身的特点和难点.由于各相间的相互作用，存在时间和空间上随机可变的相界面，其动力学性质、相间质量和热量传递的差异很大.在以往的气固、气液两相系统流动特征的分析和识别研究中，许多研究者采用统计[4-7]、频谱[4-9]、混沌[4，5，7，9-10]等信号处理方法.近年来，小波分析因具有多分辨率和良好的时间-频率双局部化特征的优点，在气液、气固两相流动特性的研究中，得到了广泛关注[11-14].Yang 等[11]运用小波分析，提取气液两相L阀压力信号的宏观尺度、中尺度和微尺度信息，发现中尺度能量随气速的增大而减小，这表明系统内的大气泡在消失，固体颗粒的循环流动加强;Luo等[12]运用小波分析，提取气液两相气升式反应器的压力脉动信号在不同频带上的局部动态特性，有效地识别到2个流型转变点.王嘉骏等[13]运用小波分析，分析气固搅拌流化床的压力脉动信号，发现随着搅拌转速的增大，散式流态化的气速操作范围线性增加.在气液固三相流动特性的研究中，Wang等[15]运用小波分析，分析气液固三相浆态床的压力脉动信号，并对小波信号进行R/S分析，发现中尺度信号具有双分形特性.在气液固三相流型的研究工作中，应用小波分析表征流型的研究工作开展的比较少.

为此，本文在横截面0.1 m×0.01 m、高0.8 m的三相流化床实验装置上，开展了应用小波分析特征参数定量表征流动结构的研究.实验中空气、水和粒径为48 μm的玻璃粉分别作为气相、液相介质和固体实验物料，对实验采集的压差脉动时间序列采用小波分析方法进行分解，得到不同尺度小波信号标准差和小波熵，定量表征不同操作参数下，三相流化床中均匀流、过渡流和非均匀流3种流型对应特征值的变化规律.

1 实验装置

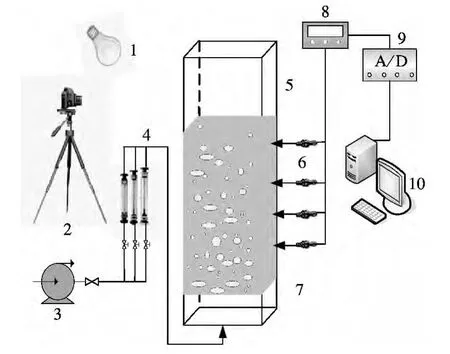
图1 实验系统流程简图

实验装置如图1所示，主要由三相流化床实验台、数据采集系统、图像采集系统构成.三相流化床的主体由透明有机玻璃制成，横截面尺寸为0.1 m×0.01 m，床高0.8 m，布风板由过滤精度为50 μm的金属烧结板制成.实验环境为常温常压.三相流化床以空气为气相，水为液相，玻璃粉为固相.在离布风板的垂直高度40，90，140，490 mm处分别布置了4个测压孔.液体压差传感器(量程为－2.5～2.5 kPa，精度为0.2%)一端与测压孔相连，另一端与压差变送器相连，输出信号经过A/D转换后，将压力波动信号转换为电信号，再由计算机将之转化为相应的压力波动值.实验过程中，在新闻镁光灯的照射下，使用高分辨率数码相机，记录不同工况下床内的流型变化情况.实验工况如表1所示.

表1 实验工况

2 压力脉动信号的小波变换原理

小波变换是分析非平稳信号和瞬态信号的时频分析工具，可分为离散小波变换和连续小波变换2种.连续小波变换主要用于理论分析，在实际的应用计算中，一般应用离散小波变换.本文采用一维离散小波变换和Mallat算法[16]，即先对较大尺度的信号进行小波变换，再选取其中的低频部分在原尺度的1/2尺度上再进行小波变换.

对于三相流化床内任一组离散的压力时间序列 X={x1，x2，…，xN}，其小波信号的计算为

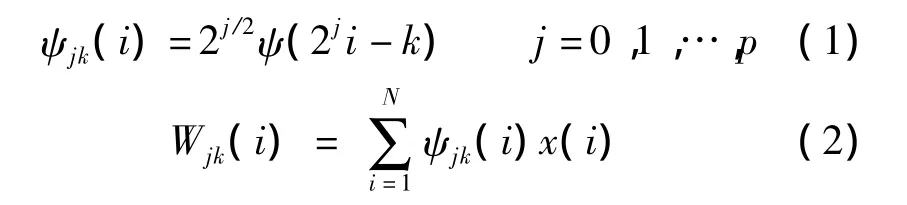
式中，k=2j，j为二进尺度参数，k为二进位移参数;i为时间序列的下标号;p为尺度最大值，p=log2N.

小波分解信号后，较大尺度、低频部分的信号是近似信号，较小尺度、高频的信号是细节信号.尺度j上的小波能量可以表示为

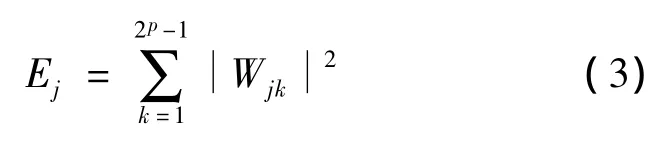
归一化后的能量Gj在尺度j上的计算为

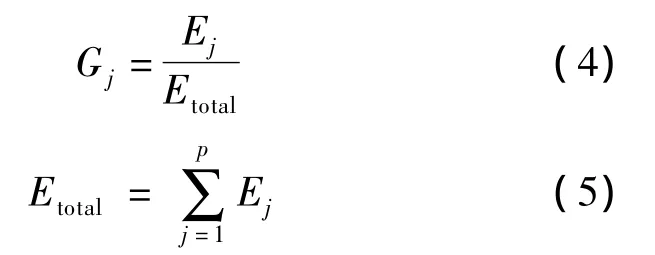
式中，Etotal为所有尺度上的能量总和.归一化的能量反映了能量在不同尺度上的分布概率.为了研究其分布特性，引入信息论中的Shannon概念[17]，小波熵S定义为

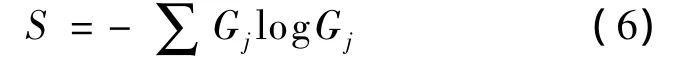
本文针对三相流化床的压力脉动信号进行一维离散Daubeehies2小波5层分解，然后对分解后的压力信号的细节信号与近似信号求标准差和小波熵，尝试运用小波信号标准差和小波熵定量表征三相流化床的流型.

3 实验结果与讨论

3.1 三相流化床的流型

图2为三相流化床的流型示意图，从图中可以观察到，3种流型具有不同的流动特性.Boyer等[18]和 Ruthiga 等[19]对这 3 种流型进行了描述和定义，并且得到了国内外研究者的认可.图2(a)～(c)依次为均匀流、过渡流和非均匀流，其中均匀流主要特点是气泡大小比较均匀，形状较规则，没有气泡的聚并、破裂发生;过渡流的主要特点是气泡的尺寸分布范围比较广，不规则气泡数目明显增多;非均匀流的主要特点是大量不规则气泡，气泡产生、聚并、破裂频繁发生.实验中拍摄到3种流型的图片，图3(a)、(b)为均匀流，图3(c)、(d)为过渡流，图3(e)、(f)为非均匀流.根据所拍摄的图片，确定三相流化床流型的2个转变气速分别为0.047 2 和0.244 m/s.

3.2 小波分析表征流型特征

图2 三相流化床的流型示意图

图3 三相流化床的流型

采集表观气速 Ug分别为 0.025，0.111，0.278 m/s下的压力脉动信号值，分别对应了三相流化床中均匀流、过渡流和非均匀流3种流型下的压力脉动情况.对实验采集的这3种流型的压力脉动信号进行Daubeehies2小波5层分解，分解后得到不同尺度的小波信号.d1，d2为微尺度高频信号，频率带范围分别为250～500 Hz和125～250 Hz，反映颗粒的高频波动;d3，d4，d5为中尺度中频信号，频率带范围分别为62.5～125 Hz，31.25～62.5 Hz和15.625～31.25 Hz，反映气泡与液-固相之间的相互作用;d6为宏观尺度低频信号，频率带范围为0～15.625 Hz，反映气泡的整体运动情况.其中，微尺度信号d1，d2为高频信号，包含高频噪音，影响流型的表征.

图4为均匀流的小波分解结果图，小波信号d6的波动最为剧烈，其波动幅值是其他尺度信号的2倍以上，说明三相流化床的压力信号频率主要集中在小于15.625 Hz的范围内，气泡是产生压力脉动的主要原因.3种流型的小波信号幅值范围不同，均匀流时，d3小波信号幅值为 －5～5，d4为－10～10，d5为 －20～20，d6为 －50～50;过渡流时，d3小波信号幅值为－10～10，d4为－50～50，d5为 －50～50，d6为 －200～200;非均匀流时，d3小波信号幅值为－100～100，d4为－500～500，d5为－1 000～1 000，d6为 －2 000～2 000.3种流型的不同尺度小波信号波动幅值依次增大，主要原因是三相流化床内部的气泡行为越来越复杂，气泡相与液-固相的相互作用也变得更为复杂，宏观稳定性较差.

图4 均匀流时的小波5层分解结果(Ug=0.025 m/s)

表观气速分别为0.025，0.111，0.278 m/s时，对应的均匀流、过渡流、非均匀流的小波信号归一化能量如图5(a)所示.由图可知，3种流型各尺度的能量分布差别不明显，其能量都主要集中在小波信号d6上，能量分布达到90%以上.

由图5(b)可知，中尺度能量所占份额达到7%以上，微尺度能量小于3%.说明三相流化床的能量主要分布在宏观尺度和中尺度上，数量达到97%以上.

对不同尺度的小波分解信号求标准差，其结果如图6所示，小波信号的标准差随表观气速的变化具有不同的特点，对这些时间序列的小波信号标准差进行分析，则有可能建立流型与小波信号标准差之间的联系.

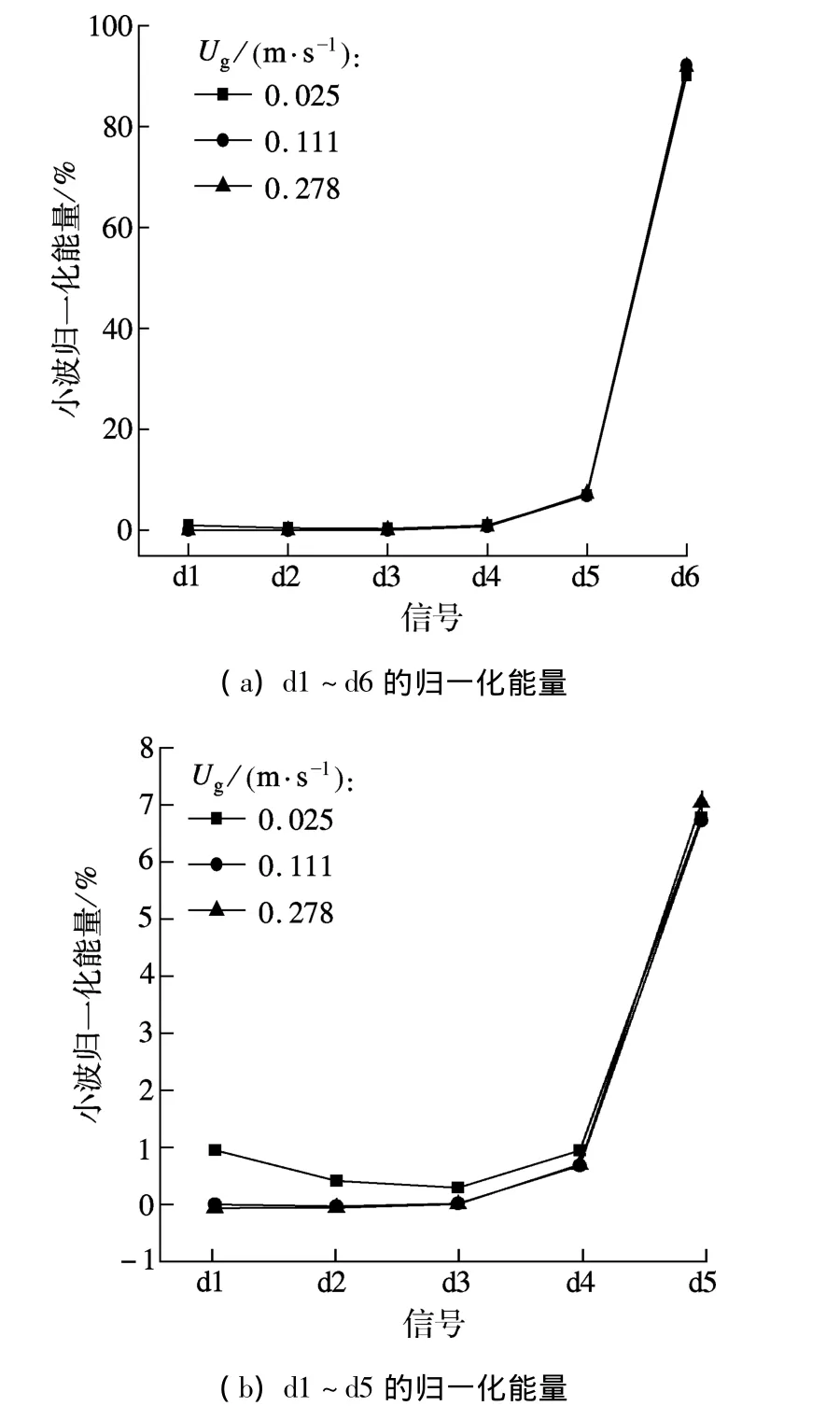
图5 不同流型的小波信号归一化能量

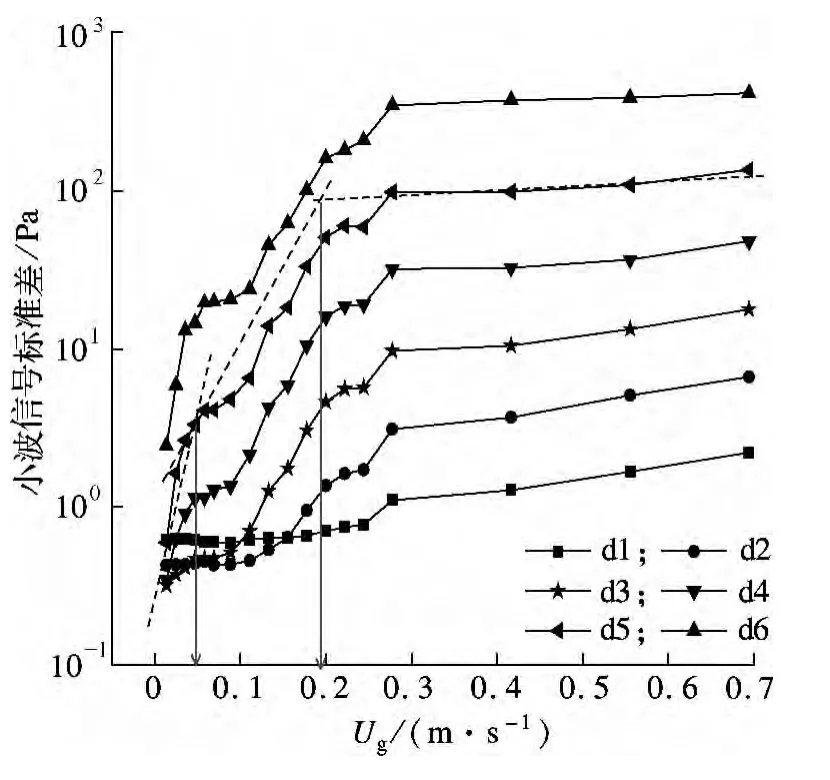
图6 不同表观气速的小波信号标准差半对数图

图6为不同表观气速的小波信号标准差半对数图.从图中可以看出，微尺度信号d1，d2的标准差在非均匀流时明显大于另外2种流型，在均匀流与过渡流时d1，d2标准差有部分重叠，这不利于流型的表征;中尺度信号d3，d4，d5和宏观尺度信号d6的小波标准差范围，3种流型都不同，所以可以把这2个尺度的信号作为3种流型表征的特征参数.对中尺度、宏观尺度的信号做进一步分析，图6中4条曲线的趋势基本一致，即液-固相与气泡相间的相互作用、气泡行为均增强或减弱，所以可以统一起来进行分析.从d3至d6，其标准差越来越大，d3，d4，d5标准差的数量级为几十，d6的标准差为最大，达到几百的数量级，主要原因是气泡的行为越来越复杂，而气泡行为是压力脉动的主要因素.

当Ug＜0.047 2 m/s时，三相流化床的流型为均匀流，小波信号d1～d6的标准差均有小幅度的增大，初始阶段，表观气速比较低，固体没有被完全流化，颗粒波动弱，气泡大小均匀，标准差比较小，但随着表观气速增大，颗粒波动、气泡与液-固相之间的相互作用均有微弱地增强，气泡数目也在逐渐增多，所以标准差有小幅度的增大.当0.047 2 m/s＜Ug＜0.244 m/s时，流型为过渡流，小波信号d1～d6的标准差显著增大.主要原因是颗粒波动、气泡与液-固相之间的相互作用均显著增强，气泡大小分布不均，小气泡聚并为大气泡，且存在少量的气泡产生、破裂、聚并现象.当表观气速Ug＞0.244 m/s时，流型为非均匀流，小波信号标准差增加比较缓慢，达到一个较稳定的状态.三相流化床系统内部气泡的聚并、破裂的情况剧烈发生，但其内部的不同尺度间的相互作用却逐渐趋于一种平衡态.

由前面的分析可知，3种流型的能量都主要集中在宏观尺度、中尺度上，小波熵能够反映不同尺度的能量分布的细微差别，小波熵值越大，不同尺度的能量分布越均匀.

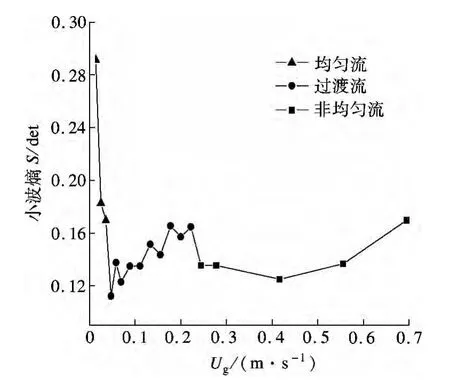
图7 不同表观气速的小波熵

图7中，当Ug＜0.047 2 m/s时，三相流流型为均匀流，小波熵值范围为0.169 6～0.291 3 det，随着气速增加，小波熵值减小，可能原因是三相流化床内气泡数目逐渐增多，各个尺度的能量分布变得不均匀，能量概率分布也变得越来越不均匀.当0.047 2 m/s＜Ug＜0.244 m/s时，三相流流型为过渡流，小波熵值范围为0.112 1～0.165 4 det，小波熵呈现有波动地缓慢增大的趋势，气泡数量和大小逐渐增加，由于复杂的气泡运动行为产生的压力脉动信号随机性和不确定性程度也随之不断增强.当Ug＞0.244 m/s时，三相流流型为非均匀流，小波熵值范围为0.125～0.169 2 det，小波熵缓慢增大，但在一定范围内趋于相对稳定，三相系统内部复杂运动逐渐达到一种平衡.对比3种流型的小波熵值范围可知，均匀流的小波熵值的范围与其他2种流型相比要大一些.

与小波信号标准差相比，小波熵参数对均匀流、过渡流、非均匀流这3种流型的定量表征的参数值范围有部分重叠，而宏观尺度、中尺度信号的小波信号标准差参数对3种流型的表征范围值没有重叠部分，能够更好地定量表征这3种流型.

4 结论

1)三相流化床的压力信号频率小于15.625 Hz，且97%以上能量集中分布在宏观尺度、中尺度上;宏观尺度、中尺度信号的小波分析，能够很好地表征均匀流、过渡流、非均匀流3种流型.

2)微尺度信号为高频信号，包含高频噪声信号，影响流型表征，对流型的表征不利.

3)与小波熵相比，小波信号标准差能够更好地表征均匀流、过渡流、非均匀流3种流型，并确定某工况下流型之间的转变气速.

References)

[1] Ishibashi H，Onozaki M，Kobayashi M，et al.Gas holdup in slurry bubble column reactors of 150 t/d coal liquefaction pilot plant process[J].Fuel，2001，80(5):655-664.

[2] Krishna R，Sie S T.Design and scale-up of Fischer-Tropsch bubble column slurry reactor[J].Fuel Processing Technology，2000，64(1):73-105.

[3] Arumugan A，Sabarethinam P L.Performance of a three-phase fluidized bed reactor with different support particles in treatment of dairy waste water[J].Engineering Apply Science，2008，3(5):42-44.

[4] van Ommen J R，Sasic S，van der Schaaf J，et al.Time-series analysis of pressure fluctuations in gas-solid fluidized beds—a review [J].International Journal of Multiphase Flow，2011，37(5):403-428.

[5] Sasic S，Leckner B，Johnsson F.Characterization of fluid dynamics of fluidized beds by analysis of pressure fluctuations[J].Progress in Energy and Combustion Science，2007，33(5):453-496.

[6] Al-Masry W A，Ali E M，Al-Kalbani M N.Prediction of regime transitions in bubble columns using acoustic and differential pressure signals[J].Chemical Engineering Journal，2007，133(1/2/3):139-149.

[7] Freitas L A P，Dogan O M，Lim C J，et al.Identification of flow regimes in slot-rectangular spouted beds using pressure fluctuations[J].The Canadian Journal of Chemical Engineering，2004，82(1):60-73.

[8] Wang Chunhua，Zhong Zhaoping，Li Rui.Flow regime recognition in the spouted bed based on Hilbert-Huang transformation[J].Korean Journal of Chemical Engineering，2011，28(1):308-313.

[9] Luo Lijia，Yan Ying，Xie Ping，et al.Hilbert-Huang transform，hurstand chaotic analysis based flow regimeidentification methods for an airlift reactor[J].Chemical Engineering Journal，2012，181-182:570-580.

[10] Wang Chunhua，Zhong Zhaoping，Jiaqiang E.Flow regime recognition in spouted bed based on recurrence plot method [J].Powder Technology，2012，219:20-28.

[11] Yang T Y，Leu L P.Multi-resolution analysis of transform on pressure fluctuations in an L-valve[J].Internationl Journal of Multiphase Flow，2008，34(6):567-579.

[12] Luo Lijia，Yan Ying，Xu Yuanyuan，et al.Time-frequency analysis based flow regime identification methods for airlift reactor[J].Industrial＆ Engineering Chemistry Research，2012，51(20):7104-7112.

[13] 王嘉骏，张文峰，冯连芳，等.气固搅拌流化床压力脉动信号的小波分析[J].化工学报，2007，57(12):2854-2859.Wang Jiajun，Zhang Wenfeng，Feng Lianfang，et al.Wavelet analysis of pressure fluctuation in agitated fluidized bed[J].Journal of Chemical Industry and Engineering，2007，57(12):2854-2859.(in Chinese)

[14] Park S H，Kim Sang D.Characterization of pressure signals in a bubble column by wavelet packet transform[J].Korean Journal of Chemical Engineering，2003，20(1):128-132.

[15] Wang Xingjun，Hu Lishun，Shen Junjie，et al.Multiscale and multi-fractal analysis of pressure fluctuation in slurry bubble column bed reactor[J].Journal of Central South University of Technology，2007，14(5):697-700.

[16] 董长虹，高志，余啸海.Matlab小波分析工具箱原理与应用[M].北京:国防工业出版社，2004:34-36.

[17] Rezek I A，Roberts S J.Stochastic complexity measures for physiological signal analysis[J].IEEE Transactions on Biomedical Engineering，1998，45(9):1186-1191.

[18] Boyer C，Duquenne A M，Wild G.Measuring techniques in gas-liquid and gas-liquid-solid reactors[J].Chemical Engineering Science，2002，57(16):3185-3215.

[19] Ruthiya K C，Chilekar V P，Warnier M J F，et al.Detecting regime transitions in slurry bubble columns using pressure times series [J].AIChE Journal，2005，51(7):1951-1965.