水平极化层MT 激电效应的模拟研究
2014-03-15梁光河蔡新平李志远谷丙洛
符 超 梁光河 蔡新平 李志远 谷丙洛
(1.神华地质勘查有限责任公司,北京市东城区,100085;2.中国科学院地质与地球物理研究所矿产资源研究重点实验室,北京市朝阳区,100029)
1 引言
1974年Hunter Ware在博士论文中首次对利用天然场源作激电法的可能性进行了理论探讨,但限于当时的观测技术,他的理论预见未能在野外试验中实现。1978年我国物探工作者吴汉荣和王式铭基于对我国华北地区天然电磁场强度和岩矿石产生激电效应条件的分析,讨论了利用天然场源作激电测量的可能性,指出关键在于提取由天然场源所引起的激电效应的技术。1982年印度学者S.Murali认为有可能利用极低频 (ELF)天然电场作为频率域激电研究的场源。90 年代中期,中国地质大学 (北京)开展了 “被动源激发极化法”研究。他们基于自己的理论和野外试验结果,对利用天然场源作激电法的前景做了乐观的估计。Erika Gaperikova和H.Frank Morrison等也进行了天然场源激电法的研究,得出了肯定的结论。罗延钟等认为从导电和电磁效应异常中提取弱小激电异常的难度极大,现有方案都不具有普遍的可行性,天然场源激电法的实际应用前景不容乐观。
李金铭等对三层极化水平层上天然场源激电测深做了理论计算,并对比了野外实测资料,效果明显。杨进等对被动源激发极化法场源的基本性质、激发极化效应的提取方法进行了讨论,以野外试验结果为例研究了矿体与异常的对应规律,对该方法的有效性和可行性进行了说明。岳安平等对一维层状介质做了MT 激电效应研究,对不同类型电阻率分布模型进行了理论计算,实验结果表明视电阻率比值和视相位比值存在明显异常。
激发极化法是一种天然场源的勘探方法,探测深度大,但由于激电法其本身的信号较弱,在实际应用中由于电磁效应等影响勘探效果不是那么理想。但是通过现阶段的理论模型计算以及野外试验结果证明该方法还是有着一定的应用前景。
2 Dias模型激电效应
岩矿石的激电响应模型比较成熟的有Dias模型和Cole-Cole模型及其组合 (复Cole-Cole模型)。本文采用Dias新模型,相对于Cole-Cole模型其拟合精度和参数物理意义更具优势。图1为Dias模型等效电路图,Dias 模型理论公式见式(1):

其中
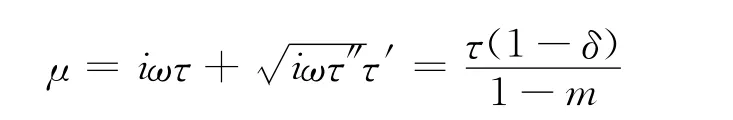
式中:ρ0 ——未考虑激电效应的直流电阻率;
ω——圆频率;
τ=rCdl——时间常数,与极化的颗粒大小有关;
τ;η=a/r——电化学参数,表示感应电流与扩散电量的相对关系;
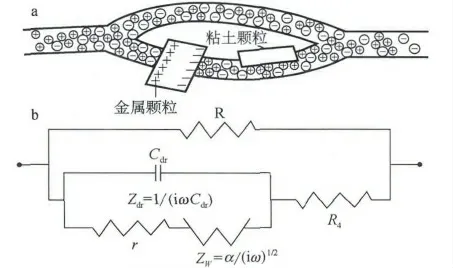
图1 Dias模型矿化岩石单元及等效电路图
3 理论模拟结果
3.1 均匀介质的理论模拟结果
图2为均匀半空间的视电阻率和视相位曲线随充电率m 变化时的计算结果。当m =0 时,电阻率和相位不随频率变化,皆为一条直线;当m ≠0时,随频率视电阻率值有所变化。可见随频率增大,视电阻率值递增速度较快;高频段即浅层极化效应被充分压制。
3.2 水平层状模型模拟结果
3.2.1 两层模型正演
图3为两层模型正演,图3-a及图3-b中h1=3000m,ρ1 =ρ2 =100Ω·M,图3-c及图3-d中h1=300m;ρ1=ρ2=100Ω·M。当浅部含极化层时,视电阻率高频部分影响较大,深层含极化层时,相位变化较大,浅部极化相位曲线出现双峰值。
图3-c及图3-d为浅层O 型地电断面的正演结果,相比3000m 的结果,激电效应对于测深曲线影响较大。浅层300 m 的测深曲线低频和高频也相差20%,这个与3000m 的结果一致。但是曲线拐点发生明显变化,浅层300 m 电阻率变化较大的频率范围由-2到2,而深层3000m 的频带较窄,并且浅部300 m 对于相位曲线的影响要比深部的大。

图2 均匀模型视电阻率ρT 和视相位φT 曲线-归一化,ρ0 =100Ω·M
3.2.2 三层模型中间极化模型正演
以三层水平低层只有中间层为极化层的模型为例,对5种电阻率断面进行了理论计算。计算时取第一层厚度h1=200m,第二层厚度h2=400m;m1=m3=0,m2=0.5和m2=0;τ=0.5s,η=9 S-1/2,δ=0.2;ρ*T 为含有极化层的视电阻率,ρT 为不含极化层的视电阻率,φ*T 为含极化层的视相位,φT为不含极化层的视相位;并且BρT =ρ*T/ρT ,BφT=φ*T/φT 。
(1)O 型地电模型 (ρ1 =ρ2 =ρ3)
O 型地电模型相当于均匀半空间,视电阻率图类似,形态基本一致,但略有区别,相位曲线基本一致。
图4-a及图5-b中 (h1=200m,h2=400 m;ρ1=ρ2=ρ3=100Ω·M),视电阻率类型正弦波变化,相位曲线在中频段变化较大,在低频段相当于直流供电,因此电阻率接近不含极化层的地层电阻率。相位变化也较大,在lgT/s=-2时相位最低可以达到39°,急剧变化,在lgT/s=1 时为47.5°,这个周期范围也对应着中间极化层的趋肤深度的位置,因此含有中间极化层对于测深曲线的形态影响较大。
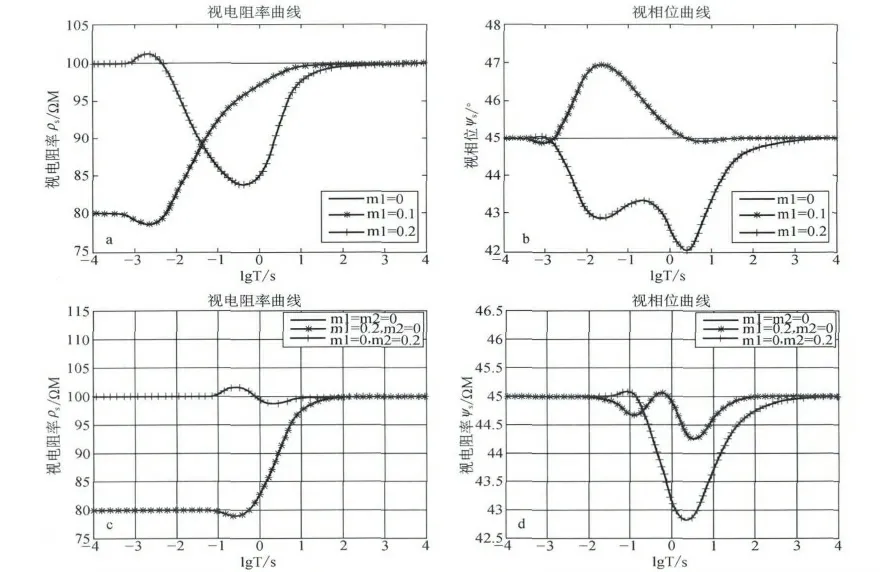
图3 两层模型O 型视电阻率ρT 和视相位φT 曲线
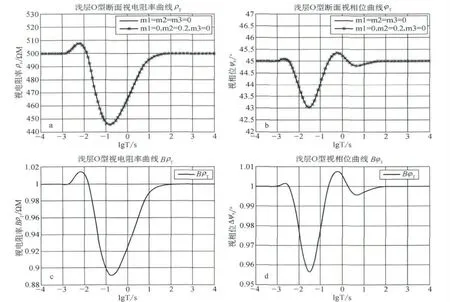
图4 三层模型O 型正演结果图
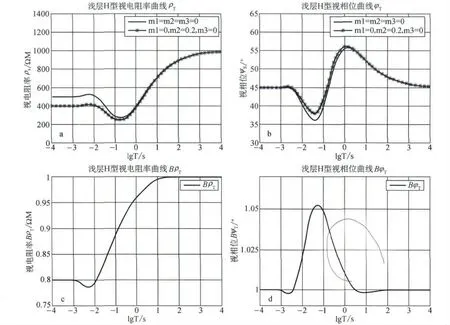
图5 三层模型H 型正演结果图

图6 三层模型A 型正演结果图
图5-c及图5-d中 (h1=200m,h2=400 m;ρ1 =ρ2 =ρ3 =100Ω·M)视电阻率比值BρT最大有30%的差别,差别较大;相位比BφT 约为3%。
(2)H 型地电模型 (ρ1 >ρ2 <ρ3)
图5中h1=200m,h2=400m;ρ1=100Ω·M,ρ2 =10Ω·M,ρ3 =1000Ω·M,图5-a及图5-b极化时视电阻率和相位在低频段差别较大;图5-c及图5-d中视电阻率比值BρT 最大为25%;BφT 为18°,差别较大,说明对于H 型地电模型中间极化的探测是有利的。
(3)A 型地电模型 (ρ1 <ρ2 <ρ3)
图6中h1=200m,h2=400m;ρ1=100Ω·M,ρ2=500Ω·M,ρ3=1000Ω·M,图6-a及图6-b极化视电阻率和相位曲线与不极化时的曲线形态很相似,单由曲线形态来判别极化比较困难。
图6-c及图6-d中曲线视电阻率比值BρT 和视相位比值BφT 变化较大,BρT 最大可以达到17%,相比BρT ,相位比值BφT 最大仅为6%。
(4)K 型地电模型 (ρ1 <ρ2 >ρ3)
图7 中h1=200 m,h2=400 m;ρ1 =ρ3 =100Ω·M,ρ2 =500Ω·M,图7-a及图7-b含极化层与不含极化层的视电阻率和相位曲线变化较为一致,但是含极化层时的曲线峰值相对降低,变化幅度比不含极化层时要小。
图7-c及图7-d中视电阻率比值BρT 和相位比值BφT 的最大值也比较大,分别为20%和7%,视电阻率的差值对于识别极化层也是有利的。
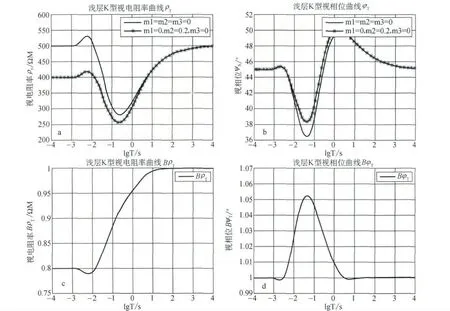
图7 三层模型K 型正演结果图
(5)Q 型地电模型 (ρ1 >ρ2 >ρ3)
图8中h1=200m,h2=400m;ρ1=100Ω·M,ρ2 =50Ω·M,ρ3 =10Ω·M,图8-a及图8-b含极化层与不含极化层时的曲线形态变化一致,但是含极化层的相位曲线有延迟之后。
图8-c及图8-d中视电阻率比值BρT 最大35%,BφT 最大为15%。这对于发现极化层是有利的。
4 正反演计算
设计模型的参数见表1,设计模型的示意图如图9所示。
4.1 激电参数反演的基本原理
常规的大地电磁测深反演方法种类较多,但是针对于激电参数的反演现阶段国内还没有较为成熟的算法。本文将根据梯度法的原理进行展开讨论。
一维层状大地电磁的正演过程都是根据底层阻抗来递推地表阻抗,从而求取视电阻率和相位,而不同频率的阻抗也是频率衰减的趋肤深度以上阻抗的反映,本质上也是一种体积效应的表现。
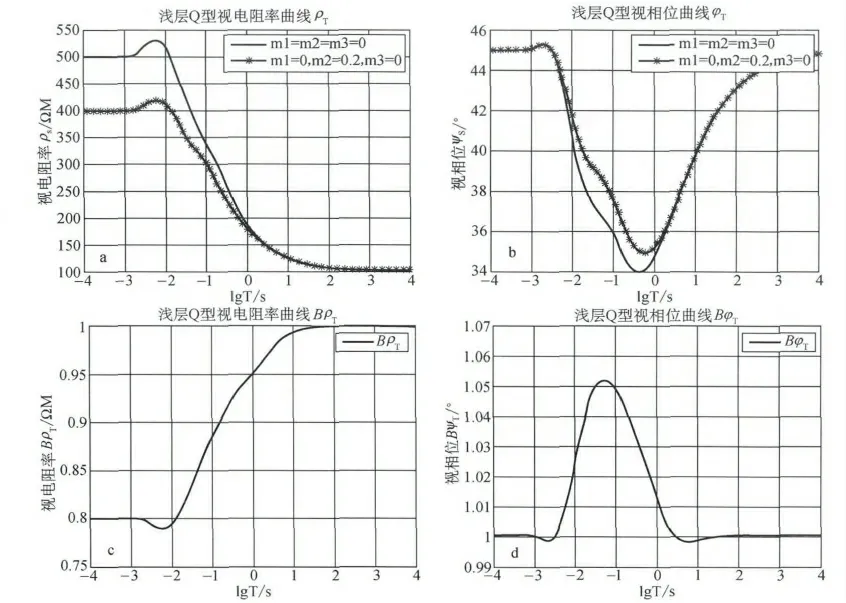
图8 三层模型Q 型正演结果图

表1 设计模型参数
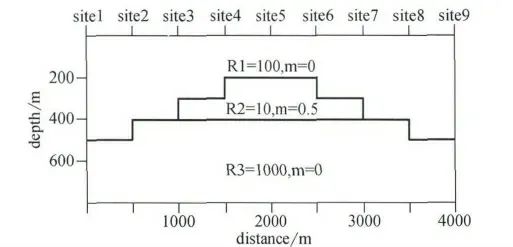
图9 设计模型图
采用一维水平层状地层递推关系进行正演计算。对于n层地电断面,设各层的电阻率分别为ρ1,ρ2 ,…,ρn ,厚度分别为h1,h2,…,hn-1,hn→∞,则地面波阻抗递推公式为:
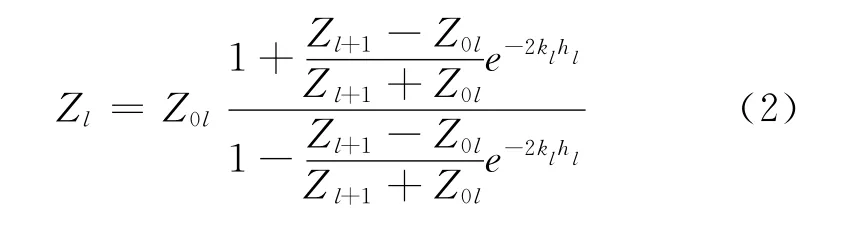
其中
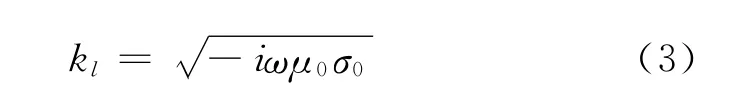
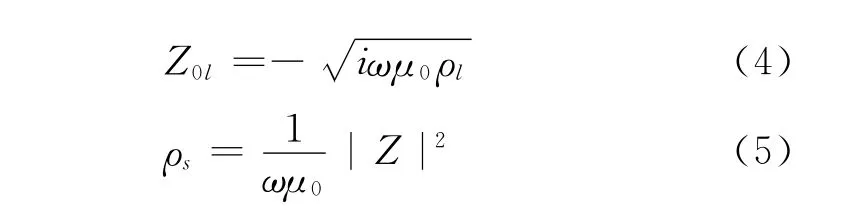
式中:kl——第l层复波数;
Z0l——l层本征阻抗;
Zl——第l层顶面的复波阻抗;
hl——第l层厚度;
ρs——视电阻率;
Z——地面波阻抗;
σl——第l层电导率。
通过式 (5),可由第l+1波阻抗递推计算第l层顶面复波阻抗,其中最底层顶面 (即半空间顶面)的复波阻抗就是半空间的本征波阻抗。
Dias复电阻率公式为:

将公式 (6)代入公式 (2)中,再将 (2)代入 (5)中,最后的视电阻率将是厚度h,时间常数τ,电化学参数η,极化电阻系数δ,充电率m和直流电阻率ρ0 的复变函数。
假设在第j个频点上的波阻抗为Z0j,则可以求出视电阻率为:

设在第j个频点的对于给定的模型参数,根据层状介质理论计算得到的视电阻率为ρmj 。可以设目标函数为:

给定的模型空间参数为h1,h2,…,hN-1;m1,m2,…,mN;ρ01,ρ02,…,ρ0N ,时间常数τ,电化学参数η和极化电阻系数δ 设为一定的常数,这样就可以根据目标函数的梯度进行寻优计算。反演方法简介如下:
(1)根据一维常规电阻率反演得出初始模型h0和ρ0 。
(2)根据初始模型缩小模型的搜索范围,利用正演程序选取合适的步长计算全局范围内的解空间。目标函数是各个频点的电阻率和相位的平方差的和。
(3)求取解空间中的最优解,分解出h、ρ 和m 。
4.2 单测点正演和反演结果
图10为设计模型的site1测点层状模型正反演的结果,site1~site9 九个测点的数据正反演拟合程度都较高。由误差结果可以看出,对于设计的模型能够得到准确的反演结果。
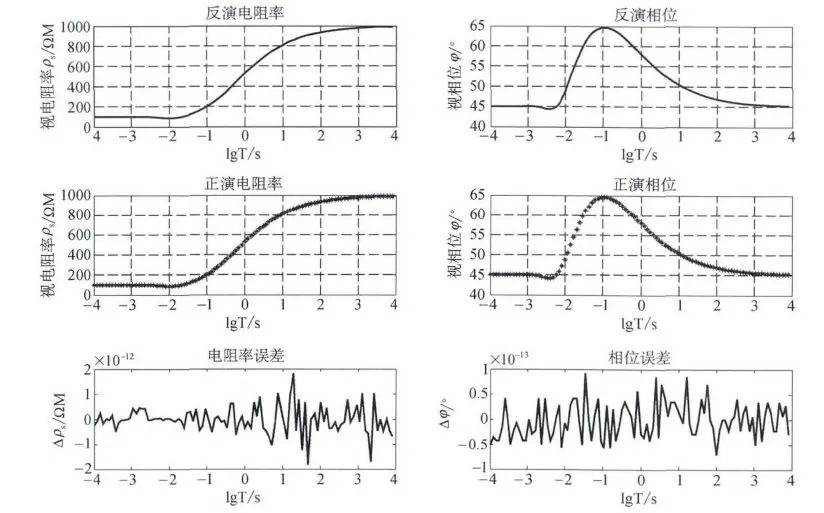
图10 设计模型site1的正演和反演结果
4.3 设计模型的反演结果
图11和图12分别反演设计模型的视电阻率和充电率结果。图11中由于测点有限,因此低阻极化体在横向上不连续,电阻率分界面上出现串珠也是因为横向测点较少插值的结果。总体上视电阻率和充电率的结果与模型的结果比较一致。

图11 反演模型的视电阻率
5 结论
文章采用Dias模型表征介质的激电效应,对不同含极化层水平地层的地电模型天然电磁场源激电测深的视电阻率及阻抗相位进行了理论计算。对比含极化层与不含极化层时相同频率的视电阻率振幅比和阻抗相位比和阻抗相位差进行了计算,并以此作为地电模型激电效应的参数,讨论了不同层中不同极化层之间的差别,实验结果显示存在极化层时的视电阻率和阻抗相位会发生变化并且和极化层的埋深、频率和极化率有很大的关系,并且对于每一种模型进行了详细的讨论。
(1)中间层极化模型中,随着极化层的深度增大,视电阻率曲线形态不变,峰值对应的频率下降,这也进一步验证了大地电磁测深的原理所在;视电阻率、相位、视电阻率比值和相位比值随着极化层埋深增大,峰值变小,峰值对应的频率降低,异常频带范围变窄。
(2)对于m=0.1和m=0.5两种充电率以及不同厚度10m 和100m 的实验结果显示,高充电率在薄层和厚层的情况下,视电阻率比值和相位比值都较大,对于识别极化层比较有利;而对于低充电率厚层的识别仅仅H 和Q 型地电断面的比值约为8%,有一定参考作用。
(3)对于各种地电模型,H 型是最有利于识别极化层的地电模型,其次为O 型和Q 型,最后是K 型,A 型相对来说比较难于识别。
(4)极化层的厚度与BρT 和BφT 基本呈线性关系,BρT 随着随着厚度增加而增大;O 型、H型、A 型、K 型和Q 型中BφT 随着厚度增加而增大,但是在H 型断面中随着峰值频率降低。
(5)极化层的埋深与BρT 和BφT 的变化也是呈线性的,在厚度小于1000 m 时,BρT 和BφT 随着埋深的增大而迅速减小。并且异常峰值对应的频率也随埋深的增大减小,但是当埋深大于2000m时,峰值频率变化趋于稳定。
(6)对于设计的模型 (图9)进行了正演的反演,误差较小,搜索的结果非常的准确。对于含极化层和不含极化层的模型分别进行了二维正演 (基于层状模型),视电阻率和相位的形态不发生变化(图11和图12),这也是我们在实测资料中很难去识别激电效应的原因。提供了视电阻率比值和相位比值的比较方法,结果证明这种方法对于识别极化层是有效的 (图12)。反演的视电阻率和充电率与模型的结果也比较一致。
[1] 吴汉荣,王式铭.利用天然电磁场进行激发极化法测量的可能性 [J].物探与化探,1978 (1)
[2] 罗延钟,张胜业,熊彬.天然场源激电法的可行性[J].地球物理学报,2003 (1)
[3] 李金铭,陈清礼,杨冠鼎等.极化水平层上天然场源激电测深的理论研究 [J].物探与化探,2003 (4)
[4] 杨进,刘兆平.天然场激发极化法在多金属矿区的野外试验效果 [J].地学前缘,2008 (4)
[5] 岳安平,底青云,王妙月.油气藏MT 激电效应一维正演研究 [J].石油地球物理勘探,2009 (3)
[6] 杨进,谭捍东,傅良魁.被动源激发极化法的野外试验结果 [J].现代地质,1998 (3)
