采用拥挤收费的机场时刻管理多用户双层规划模型

王 琨，朱金福，高 强

(南京航空航天大学民航学院，211106南京)

航班时刻是指向某一航班提供或分配的在某一机场某一特定日期的到达或起飞时刻.2006—2011年间，全国机场航班起降架次平均年增幅超过10%，旅客吞吐量1 000万人次以上的枢纽机场或干线机场都出现不同程度的时刻紧张，对航班正常运营造成影响.2011年全民航航班正常率仅为77.2%［1］，其中27.5%的航班延误是由于流量控制原因造成的.大量航班延误使得繁忙机场运营效率降低，给航空公司也带来巨大损失.但由于机场保障容量的限制，繁忙机场无法通过临时增加容量来解决时刻紧张问题，一种有效的解决办法是对现有时刻资源进行优化配置和有效管理.目前我国对航班时刻采用祖父制和先到先得的分配规则，而在美国等国家开始对航班时刻采用市场化分配模式，通过需求管理促使部分效率低的航班从高峰时刻向非高峰时刻转移，从而改善机场的延误情况，在尽量满足需求的同时，提高机场的总体运营效率.

交通需求管理主要应用于城市道路交通，国内外关于拥挤收费的研究已较为丰富，陈来容和张岚［2］建立了路网综合效能最大化为目标的双层规划拥挤定价模型，利用遗传算法确定拥挤收费的费率.张华歆和周溪召［3］研究了多种特性的道路使用者共存模式下的交通网络拥挤道路收费模型.孙祥龙和陆建［4］则分析了公众对交通拥挤收费的心理可接受性，建立结构方程模型分析如何提高公众对拥挤收费的可接受性.陈蔚等［5］通过分析不同O-D下社会净效益的变化，对城市道路拥挤收费实施时机确定方法进行了探讨和研究.近年来交通需求管理在民航方向的应用也取得了一定进展，美国的纽约、芝加哥、华盛顿等枢纽机场对航班时刻分配采取了需求管理模式.Rui Cunha Marques等［6］研究了全球141个机场的拥挤程度以及拥挤对机场效率的影响.Vikrant Vaze和Loan Thank Le等［7-8］从航空公司的角度，研究了机场时刻需求管理模式下航空公司如何制定航班时刻竞争策略.Tracy Johnson等［9］则从机场管理的角度，分析了芝加哥机场15:00—17:00、19:00—20:00两个高峰时段的拥挤情况，考虑通过拥挤收费促使航空公司转而选择其他非高峰时刻.

由于机场时刻需求的特点［10］，道路交通需求管理并不完全适用于机场时刻管理.目前对机场时刻拥挤收费的研究也主要从单一决策者角度出发，没有综合考虑机场管理方和航空公司两个具有不同目标决策者的共同利益.本文针对繁忙机场的时刻管理，从机场管理方和航空公司两个角度考虑，在分析直达航班和联程中转航班不同特性的基础上，建立了多用户的机场时刻管理双层规划模型，并通过实例分析，验证该模型的适用性，为提高繁忙机场时刻使用效率提供了理论参考.

1 机场时刻管理多用户双层规划模型

1.1 模型背景

机场容量是根据机场保障能力和空域容量的限制综合评定的单位小时内机场能够保障的航空器最大起降架次.民航局根据容量饱和程度，把机场分为协调机场和非协调机场［11］.协调机场是指在某一特定的时间段内航班起降架次已经达到或接近机场的保障容量，需要进行时刻协调的机场.表1给出了2012年主要运输机场的旅客吞吐量［12］.

表1 2012年全国运输机场旅客吞吐量

从表1可以看出，第一类和第二类机场日平均起降航班量较大，均属于协调机场.但与第一类机场相比，第二类机场各时段起降航班量有较明显的波动，高峰时段和非高峰时段起降航班量差别较大，有一定的时刻管理和调整空间.因此本文选择第二类机场作为主要研究对象.

旅客的期望出行时刻各不相同，但存在一定的规律性，表现在需求分布曲线存在明显的高峰时段.航空公司会尽量选择旅客需求旺盛的高峰时刻安排航班，以追求更好的经济效益，因此导致机场高峰时段起降航班量超过小时容量，造成拥堵和延误.本文选取了第二类机场中的南京机场进行研究.以每30 min为一时长，将南京机场每日主要运营时间(7:00—22:00时)分为32个时段，按照民航行业的统计要求，统计得到各时段的起降航班量和平均延误时间，如图1所示，可以看出，航班量曲线和延误时间曲线呈现出较为相近的规律，即航班量大的时段，其延误时间也往往较长.如12:30—14:00、17:00—18:00等时段起降架次都达到或超过机场保障容量26架次/h，属于高峰时段，其对应的航班延误时间明显增加.

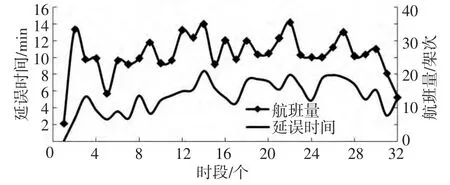
图1 南京机场7:00—22:00时起降航班量和平均延误时间

对于机场管理者而言，依靠机场扩容解决拥堵现象周期长，短期不能实现，使用行政手段强制减少高峰时段航班，会由于供需矛盾突出而工作难度大.因此采用经济手段，对高峰时刻航班收取拥挤费用，提高高峰时刻航班的运营成本，促使效率相对较低(如机型小、客座率低)的航班转而选择其他时刻，从而减少高峰时刻航班量.对于获得高峰时刻的航空公司，支付拥挤费用产生的成本低于航班延误成本，总体上是有益的.使用经济手段解决拥堵现象，并未影响旅客出行，因为选择高峰时刻的航班可采用大机型、提高客座率来满足旅客需求，提高时刻使用效率，这也符合机场时刻作为一种社会资源应该优先分配给效率最高使用者的原则.

对于高峰时刻拥挤收费问题，机场管理方和航空公司是两个不同的决策主体，具有不同的决策目标和约束条件，但决策结果又相互影响，属于双层结构的问题，需要采用双层规划模型.繁忙机场的航班可分为直达航班和联程中转航班，其在枢纽建设、延误损失等方面表现出不同的特性，需要进行多用户分析.因此本文构建了机场时刻管理的多用户双层规划模型，来解决繁忙机场高峰时刻拥堵问题.

1.2 机场时刻管理双层规划模型

模型将机场主要运营时间分为n个时段，每个时段视为航班进出港的路径，A为所有路径的集合，即{a1，a2，a3，…，an}.G为起降航班类型的集合，即{g1，g2，…，gm}.图2中，实线代表进出机场的路径，路径an上的虚线代表不同航班类型.

图2 机场时刻使用情况

机场拥挤收费可看做是机场管理者和机场时刻的使用者——航空公司两个层次共同作用的结果.上层模型的决策者是机场管理者，目标为:

1)实现机场综合收益最大化，此处收益不仅仅指经济收益，同时还包括使用效率的提高带来的社会效益，即延误减少给旅客出行带来的便捷;

2)在满足辐射区域旅客航空出行需求前提下，尽可能吸引中转航班，打造枢纽辐射型航线网络，提高机场枢纽地位.下层模型的决策者是航空公司，目标为支付的总体广义时间消耗最小.

上层模型:

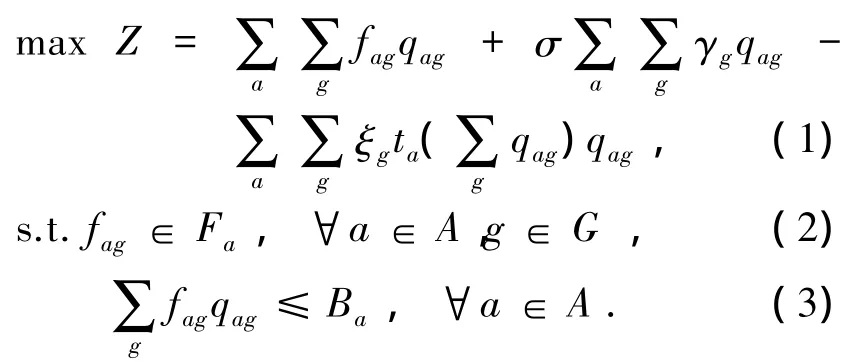
式中:fag、fag分别为路径a上第g类航班的拥挤收费费率、起降航班量;Fa为路径a上拥挤收费费率的可行域，即拥挤收费费率应当在一定的范围内，上限取最高收益路径的收益水平.下限取0，为不收费;ta(q)为路径a的延误时间函数，为单调递增函数;Ba为路径a的预期增量收益;ξg为时间-费用转换系数，即第g类航班单位延误时间的费用损失;γg为航班偏好系数，即机场对不同类型航班的偏好;σ为机场起降架次与收入之间的正相关系数.

式(1)为目标函数，其中第1项是路径a上第g类航班的总拥挤收费;第2项是航班正常起降收益，考虑了各用户对提高吞吐量、打造枢纽的贡献;第3项是总延误损失.式(2)为约束条件，考虑拥挤收费费率的范围.式(3)为约束条件，表示路径a上的拥挤收费应以该路径获得的增量收益为上限，体现了拥挤收费并不是以抑制需求为目的.

下层模型:

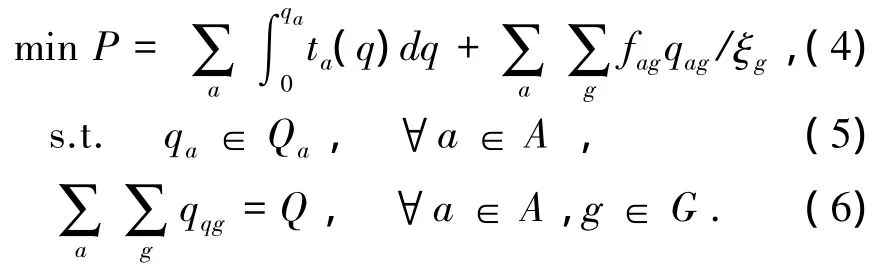
式中:qa为路径a上的航班量，为该路径上所有类型航班量之和;Qa为路径a上航班量的可行域，上限为机场最高保障容量，下限为0;Q为A集合内的需求总量，可由机场收到的时刻需求总量统计得到.

式(4)为目标函数，表示机场内起降航班的广义时间消耗最小，其中第一项是时间消耗，第二项是转换为时间的费用消耗.式(5)为约束条件，表示路径a上航班量的可行域.式(6)为约束条件，反映了保障航班总量应尽量满足航空公司的需求.

1.3 模型算法

本文利用Lingo软件，采用迭代优化算法［13］对模型进行求解.具体的算法步骤如下:

步骤1 取定上层规划的一个拥挤收费费率的初始可行解f0，设迭代次数k=0;

步骤2 将fk代入下层规划，得到解qk;

步骤3 令q*=qk，作为常量代入上层规划，求解得到fk+1;

步骤4 检验｜fk+1-fk｜＜ε，如果是，令f*= fk+1，即模型的最终解，迭代停止;否则，令

k=k+1，返回步骤2.

2 模型参数估计

2.1 航班偏好系数γg

航班偏好系数γg表示机场对不同航班类型的偏好程度，部分机场为了提高其区域影响力，扩大辐射范围，会在一定程度上希望吸引联程中转航班.直达航班作为基准航班，γ1=1.联程中转航班的偏好系数取决于机场容量的使用水平和机场枢纽化程度两个因素，可通过式(8)计算得到.

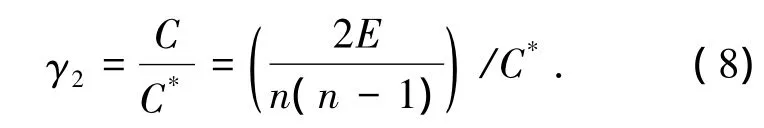
式中:C为反映机场枢纽化程度的集群系数［14］; n为该机场的通航城市数;E为与该机场通航城市间开通的航线数;C*为参照机场的集群系数，本文选取枢纽化程度较高的航线网络，取C*= 0.149.γ2＞1，γ2越大，表示与参照机场相比枢纽化程度差距越大，对联程中转航班的需求越大.

2.2 时间－费用转换系数ξg

时间-费用转换系数ξg表示不同类型航班单位延误时间的费用损失.直达航班的La可通过统计航班单位延误时间给航空公司造成的损失，即由于航班延误给航空公司造成的单位时间损失，采用民航内主要航空公司的平均数据进行分析［15］.

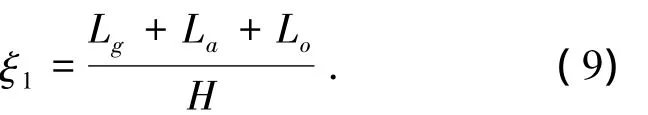
式中:Lg为航班无法起飞而在地面等待的地面延误损失，La为航班在飞行过程中发生的空中延误损失，Lo为由于航班延误导致飞机不能执行其他飞行任务而产生的机会成本，H为飞行小时.

对于联程中转航班ξ2而言，除了以上延误损失，还应包括因中转导致的后续延误损失.

式中φ为后续延误损失，为中转旅客无法衔接后续航班而发生的退票、改签等费用.

3 应用实例与分析

结合南京机场有关数据资料，本文应用以上模型进行了实例分析.路径为按照每30 min为一时长将全天主要运营时间分成的32个时段，即{a1，a2，…，a32}，用户类型分为直达航班和中转航班，即{g1，g2}.Q=330架次.Ba根据各时段航班的客座率和票价水平估计得到.γ1=1，γ2= 2.8，ξ1=0.28万元 /h，ξ2=0.54万元 /h，σ= 0.89.ta(qa)通过分析各路径的航班量和延误时间得到，测算后采用幂函数进行拟合.为便于计算，本算例考虑对航班量和延误时间均较高的a12、a16、a22这3条路径收取拥挤费用，其余路径的拥挤收费为0.f0取(0，0，…，0)，经过3～4次迭代，计算结果收敛于最优解f*，即对路径a12、a16、a22上的直达航班分别按照0.16、0.22、0.47万元的费率收取拥挤费用，这3条路径上的联程中转航班拥挤收费费率为0.图3给出了模型优化前后航班量和延误时间的对比.

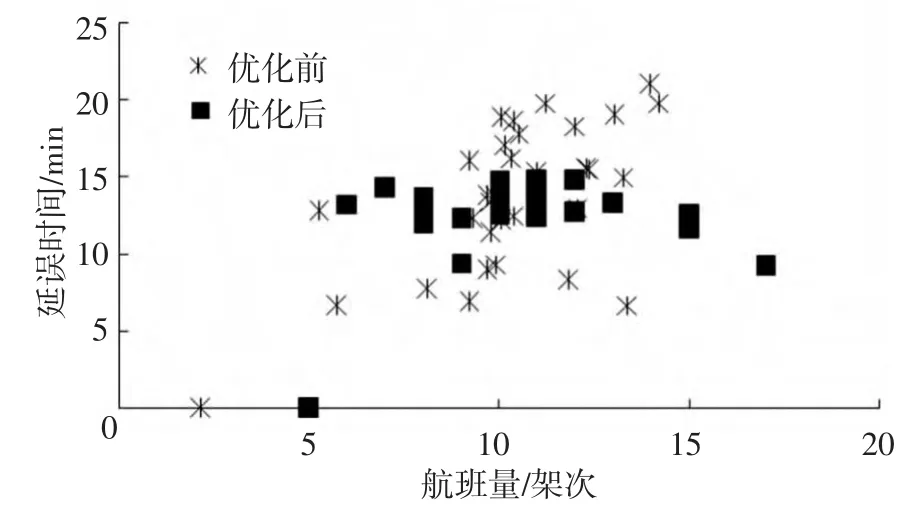
图3 优化前后各时段的航班量和延误时间对比

从上述模型计算结果可以得出如下结论:

1)根据图3可得，实施拥挤收费后，各路径航班量的波动性降低，qa的标准差由2.51降至2.32，起到了“削峰填谷”作用.与目前南京机场实际运营情况相比，平均延误时间由14.2 min降至12.8 min，机场综合收益Z增加4.3%，航空公司的总广义时间消耗P降低16.6%，达到了模型优化的目的.

2)本算例选取了最拥挤的3条路径，即a12、a16、a22上的航班计算拥挤收费费率，但实际上最终解f*仅对此3条路径上的直达航班收取拥挤费用，联程直达航班的拥挤费率为0，这表明机场希望吸引更多的联程中转航班，以加强其枢纽建设的目的.

3)图4反映了机场总拥挤收费与时刻需求总量之间的关系.可以看出，当时刻需求总量小于机场保障容量时，随着时刻需求总量的增加，总拥挤收费也在增加，说明即使收取一定的拥挤费用，也没有抑制了航空公司对高峰时段时刻的需求.当时刻需求总量逐渐接近机场保障容量时，高峰时段已经饱和，无法继续增加航班，总拥挤收费逐渐稳定.

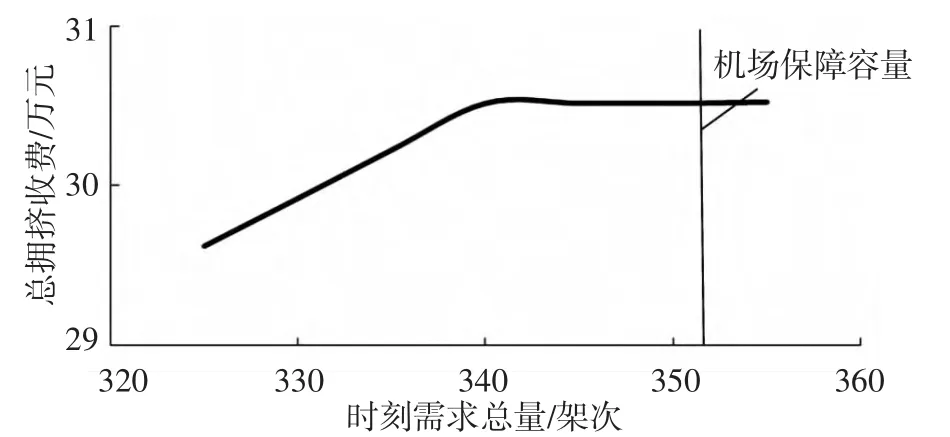
图4 总拥挤收费与时刻需求总量的关系

4 结论

1)本模型同时考虑了机场时刻管理方和航空公司对于时刻管理的目标，通过确定合理的高峰时段拥挤收费费率，促使低效率的航班向其他时段适当转移，实现系统整体航班延误水平降低，机场使用效率和广义收益提升.应用实例的优化结果表明，模型对于提高繁忙机场的时刻使用效率具有很好的效果.

2)模型的建立是基于航空公司对时刻的需求，即旅客对时刻的需求.采用经济手段对高峰时段收取拥挤费用，并没有影响航空公司对机场高峰时刻的需求，即旅客对高峰时刻的需求.

3)直达航班和联程中转航班在繁忙机场枢纽建设中作用不同，其延误损失的计算也不相同，本文针对这些特点分别进行参数分析，建立了多用户模型，使模型更符合机场运营的实际情况，提高了模型的实用性.

4)本文研究的是机场时刻需求管理的一级市场，即根据一定的规则和方法将时刻分配给航空公司，对于允许航空公司之间进行时刻再交易的二级市场中实现的航班随机延误扰动下的适应问题，将在今后做进一步的研究.

［1］2011年民航行业发展统计公报［EB/OL］.［2012-03-15］.http://www.caac.gov.cn.

［2］陈来容，张岚.基于双层规划的拥挤定价模型及算法［J］.北京工业大学学报，2006，32(6):526-529.

［3］张华歆，周溪召.多模式交通网络的拥挤道路收费双层规划模型［J］.系统工程理论方法应用，2005，14 (6):546-551.

［4］孙祥龙，陆建.基于结构方程的拥挤收费公众可接受性模型［J］.哈尔滨工业大学学报，2012，44(12): 140-144.

［5］陈蔚，杜豫川，邵敏华，等.城市道路拥挤收费实施时机确定方法研究［J］.公路工程，2008，33(5): 142-145.

［6］MARQUES R C，SIMOES P.Measuring the influence of congestion on efficiency in worldwide airports［J］. Journal of Air Transport Management，2010，(16): 334-336.

［7］VAZE V，BARNHART C.Competitive airline scheduling under airport demand management strategies［Z］. Massachusetts Institute of Technology，2010.

［8］LE L T.Demand management at congested airports:how far are we from utopia?［D］.Washington:Washington George Mason University，2006.

［9］JOHNSON T，SAVAGE I.Departure delays，the pricing of congestion，and expansion proposals at Chicago O' Hare Airport［J］.Journal of Air Transport Management，2006，(12):182-190.

［10］BRUECKNER J K.Internalization of airport congestion:a network analysis［J］.International Journal of Industrial Organization，2005，(23):599-614.

［11］民航航班时刻管理暂行办法［Z］.北京:中国民用航空局，2007.9.

［12］2012年全国机场生产统计公报［EB/OL］.［2013-03-25］.http://www.caac.gov.cn.

［13］刘伟铭.道路收费系统的优化模型及算法［M］.北京:人民交通出版社，2009.

［14］曾小舟，江可申，程凯.我国航空网络枢纽机场中心化水平比较分析［J］.系统工程，2010，28(9):39-45.

［15］邢有洪，李晓津.航空公司航班延误损失分析［J］.会计之友，2010(2):41-44.