基于机动检测的自适应实时时间配准算法∗
2014-03-14董凯,关欣,刘瑜,何友
董 凯,关 欣,刘 瑜,何 友
(海军航空工程学院信息融合技术研究所,山东烟台264001)
0 引言
在分布式多传感器融合系统中,由于传感器在工作起始时间、扫描周期、传输延迟上很难完全相同,导致融合中心接收到的航迹数据往往是异步的。因此,融合中心在进行融合处理前,通常需要将这些异步的航迹数据同步到相同的时刻上,即进行时间配准。时间配准过程是在已有数据基础上产生新的数据,不可避免会引入新的误差,如果配准误差过大,势必直接影响后续的融合处理。文献[1]采用两点直线外推的方式对机载ESM与雷达航迹数据进行配准,简单实时性好,但仅适合于目标速度均匀、航迹精度较高的场合;文献[2]给出了拉格朗日线性插值的数学描述,该方法的缺点是要求配准函数解析式通过所有已知点,这在存在随机量测误差的航迹数据中显然不是最优的;文献[3-4]讨论了最小二乘法曲线拟合时间配准方法,该方法不要求拟合曲线通过已知点,但存在拟合阶数固定的问题;文献[5]通过分段重叠处理的方式实现配准,提高了导航系统中的采样率和配准精度,但是配准时间间隔固定为配准传感器的平均值;文献[6]和文献[7]采用卡尔曼预测和H∞滤波的方法,根据目标的实时运动状态预测配准时刻位置,能够达到较高的配准精度。但是上述方法存在一个共性的问题——通常仅在某种特定机动条件下精度相对较高,而复杂环境下目标的机动形式往往是复杂多变的,因而这些方法不总是最优的。文献[8]对目标可能存在机动和非机动的模型变换情况下的时间配准进行了研究,对目标航迹序列进行不同阶次的滑窗多项式拟合,并根据拟合误差在线估计目标的运动模型并进行实时卡尔曼预测配准。该算法的问题在于真实环境下无法得到目标真值,也就无法得到不同阶次拟合结果的误差,进而无法估计目标运动模型,而且文中采用的卡尔曼预测进行时间配准,缺乏不同运动模型下的适应性。对于机动目标的跟踪,传感器通常采用可调白噪声、Singer模型、交互多模型等机动跟踪算法[9],实现对机动目标的稳定跟踪。因此,本文提出基于机动检测的自适应实时时间配准算法,融合中心根据航迹数据中的位置和速度信息检测目标机动情况并估计目标运动模型,对于不同的运动模型自适应地调整时间配准算法,有效降低时间配准误差。
1 常用时间配准算法分析
分布式融合系统对时间配准除了精度要求之外,还有实时性要求。即当各传感器以不同数据率向融合中心传输航迹数据时,融合中心将根据系统设计要求选择一定的数据率,将当前时刻已知的航迹数据配准至融合中心采样时刻。通常利用最新若干个时刻的航迹数据完成滑窗式配准,因为如果取样时刻点数越多,则目标的运动轨迹越复杂,用直线或高阶多项式曲线拟合描述的误差会越大。因此通常采用两个或三个时刻,即两点或三点滑窗式配准。
1.1 拉格朗日线性插值
内插外推法以拉格朗日线性插值[2]为例,假设目标在t1和t2时刻的位置分别为(x1,y1,z1)和(x2,y2,z2),则通过线性插值可得到目标在t时刻的位置(x,y,z)为
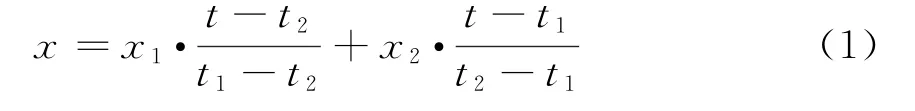
同理可得y和z表达式。该算法只需要最新两点航迹位置信息即可完成配准,实时性好。但其本质是一种代数插值法,即用插值多项式逼近真实值。它要求插值多项式通过所有给定数据点,但实际上所谓给定的雷达航迹数据本身是存在误差的,即真实值并不一定通过所有点。因此这类算法的缺点是显然的。
1.2 线性最小二乘拟合
线性最小二乘拟合[10]将已有数据拟合为直线,表达式为

式中,a和b为待定系数,满足以下条件:
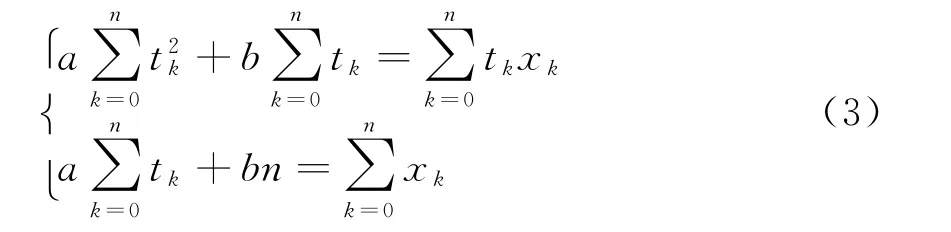
该方法需要两个以上的已知点,这里采用最新的三点位置,确定待定系数后即可求解配准时刻的位置。与内插外推法不同,最小二乘拟合法不要求拟合曲线通过所有已知点,只要求得到的近似函数能反映数据的基本关系,因此曲线拟合过程比插值过程得到的结果更能反映客观实际。采用最新的三点航迹,能够有效降低随机量测误差的影响,适合于目标为匀速运动模型时情况。
1.3 二次多项式最小二乘拟合
二次多项式拟合[3]将已有数据拟合为二次曲线,表达式为
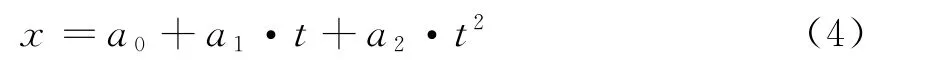
式中,系数a0,a1,a2满足如下方程组:
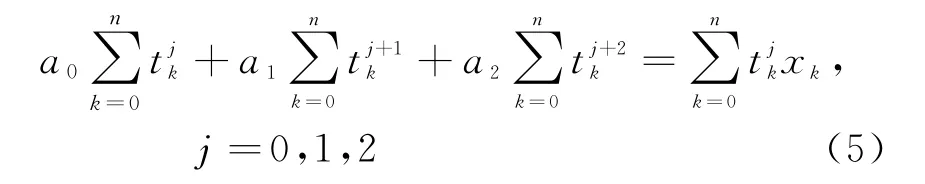
同样采用最新的三点航迹,能够有效降低随机量测误差的影响。适合于目标为加速或变加速运动模型时的机动情况。
1.4 卡尔曼预测
分布式融合系统中的局部传感器向融合中心传输的除了目标位置信息,通常还有速度信息,因此可以利用最新时刻一个航迹点的速度信息采用卡尔曼预测完成实时配准[6]。即
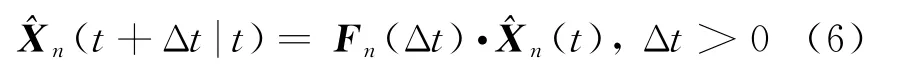
式中,F n(Δt)为n(n=2,3,4)状态向量维数的卡尔曼预测矩阵,Δt为配准时刻与目标状态估计时刻的时间差。
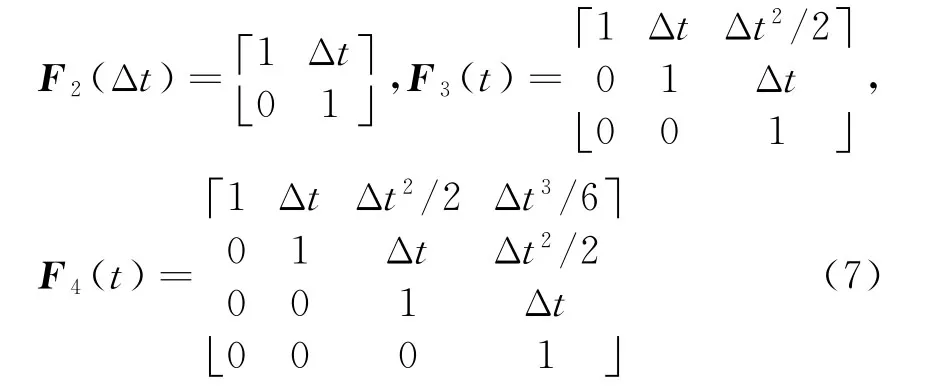
由于融合中心通常无法获得加速度信息,因此该方法对于匀速运动目标来说,可达到较高的配准精度,但对于匀加速和匀变加速运动等机动目标来说,精度会有所降低。
1.5 仿真对比
不失一般性,仿真中仅研究目标在一维x方向上分别作匀速、匀加速和匀变加速运动,目标的初始位置为10000 m,初始速度为-100 m/s,初始加速度为3 m/s2(匀加速目标),初始加速度变化率为0.1 m/s3(匀变加速目标)。传感器对目标的位置进行观测,数据周期T=3 s,量测误差标准差σ=5 m。传感器采用卡尔曼滤波对目标的运动状态进行估计,并将目标的位置和速度的估计值上报给融合中心,融合中心的融合周期T0=1 s。蒙特卡罗仿真300次,仿真时间60 s,时间配准从第10 s开始。不同目标运动模型下各配准算法的均方根误差(RMS)随时间t变化的情况如图1~3所示。
从图1~3中可见,目标处于不同的运动状态下,不同配准算法的精度不同,按照精度排序如表1所示。
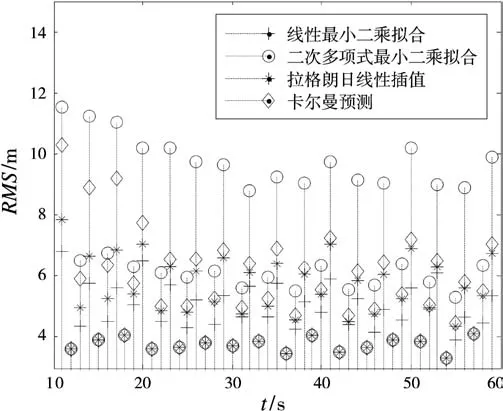
图1 匀速目标各时间配准算法误差

图2 匀加速目标各时间配准算法误差
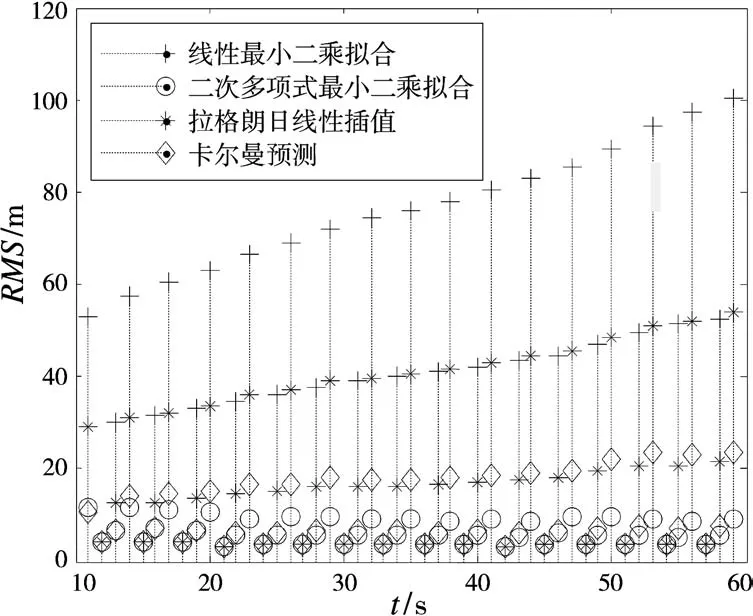
图3 变加速目标各时间配准算法误差
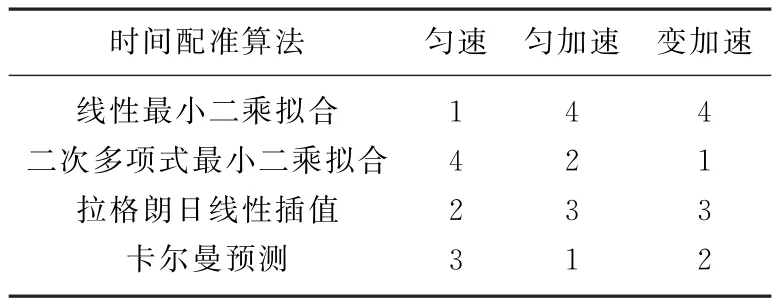
表1 不同运动模型下各配准算法精度排序
可见,拉格朗日线性插值法的精度始终不是最优的;而目标匀速运动时,线性最小二乘拟合最优;目标匀加速运动时,卡尔曼预测略优于二次多项式最小二乘拟合;目标变加速运动时,二次多项式最小二乘拟合精度最高。因此,如果固定地采用其中任意一种时间配准方法,不能保证在目标运动状态复杂多变情况下始终达到最优的时间配准。
2 算法描述
2.1 目标机动检测与模型估计
通过对以上常用时间配准算法的对比分析可知,当目标运动状态发生变化时,时间配准算法也应该相应变化,及时采用配准精度最高的算法以提高总体的配准精度。因此本文通过对目标的机动检测判断采用相应的配准算法。
雷达的机动目标跟踪算法[9]中的机动检测通过设置归一化新息平方的门限,在卡尔曼迭代滤波中判断目标归一化新息平方是否超过该门限,是则认为目标发生机动,否则认为目标为非机动状态。但是在分布式结构的融合系统中,融合中心只能得到目标位置和速度信息,而无法获得目标新息及其协方差。因此,本文提出根据目标速度信息估计目标运动模型,当加速度接近零时,认为目标运动模型是匀速,当加速度单调变化时,认为目标运动模型是变加速,其他情况则认为目标是加速,然后再根据表1所示内容切换选择采用当前运动模型下最优的时间配准算法。算法模型描述如下:
首先,融合中心利用k时刻最新三点的速度信息计算融合中心估计加速度。
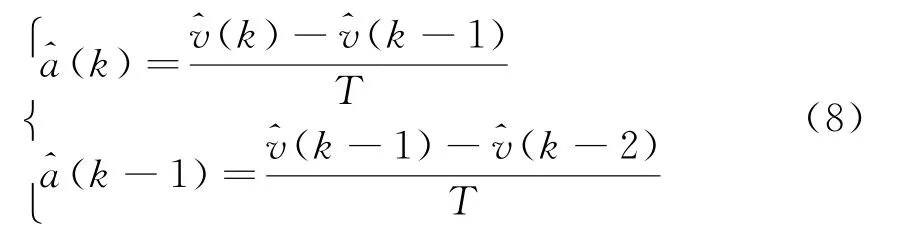
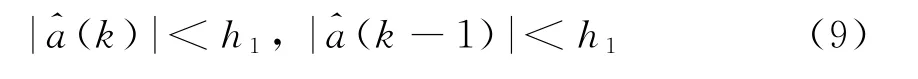
然后,如果式(9)不满足,则需进一步判断是匀加速模型还是变加速模型。同样为加速度变化率设置判决门限h2,判决式为
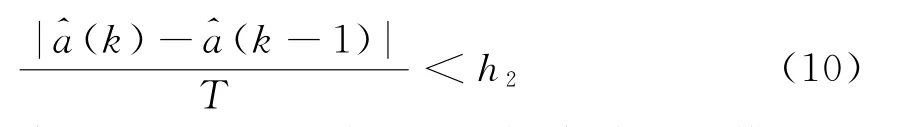
当式(10)成立,则认为目标当前运动模型为匀加速,此时选择卡尔曼预测法完成时间配准。
最后,如果加速度变化率超出门限h2,认为目标当前运动模型为变加速,此时选择二次多项式最小二乘拟合法完成时间配准。
通过以上判决,融合中心能够根据目标运动模型的变化自适应切换最优的时间配准算法,从而提高全局配准精度。
2.2 自适应时间配准
基于机动检测的自适应时间配准流程图如图4所示。
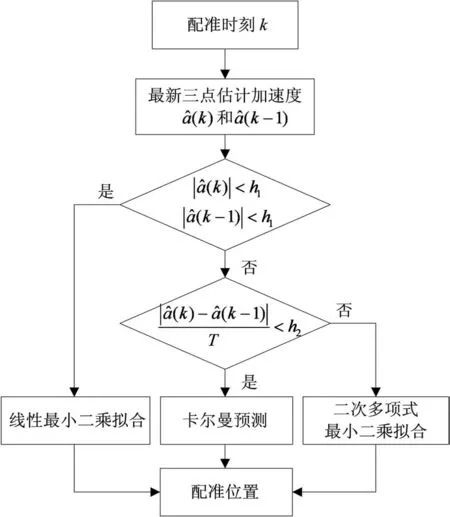
图4 自适应实时时间配准流程图
3 实验结果与分析
参照前述仿真条件,仿真时间设为70 s,误差比较从10s开始,门限h1=1.1,h2=0.7,目标的运动情况如表2所示,仿真结果如图5~图6所示,其中图5为算法对比全局图,为便于观察,图6给出对应的局部放大图。仿真时间内平均误差比较结果如表3所示。

表2 目标运动情况表
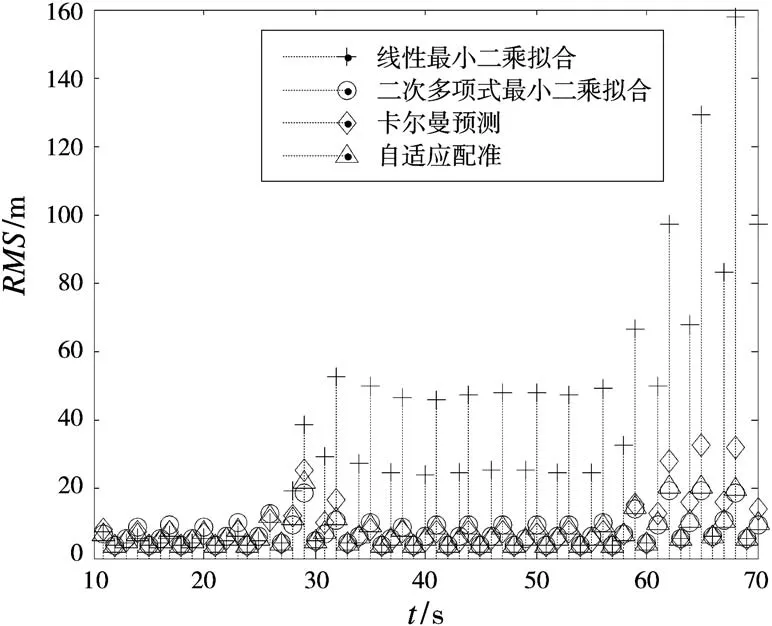
图5 各时间配准算法误差(全局)
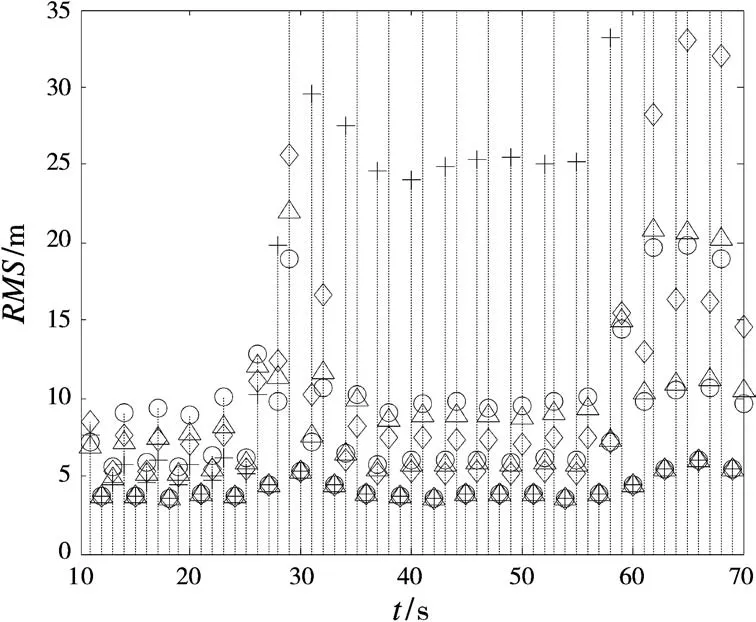
图6 各时间配准算法误差(局部放大)

表3 各时间配准算法的平均误差
从图5~图6可见,本文提出的自适应时间配准算法在目标匀速运动段的误差接近线性最小二乘拟合法,匀加速运动段接近卡尔曼预测法,变加速运动段接近二次多项式最小二乘拟合法。这样,自适应时间配准算法总体的平均误差能够优于单一地采用某一种时间配准算法。
但是需要注意的是,由于航迹数据存在滤波误差,自适应算法的门限判断并不能保证完全准确切换为目标当前运动模型,只是与其保持一致的概率较大。并且,目标机动时航迹滤波结果与真实值相比存在一定的滞后性,再加上自适应算法需要对两点数据进行差分以估计加速度,这都将给配准算法的实时切换带来一定影响。但总体来说,通常情况下目标的机动并不会十分频繁,多数时间是处于相对稳定的运动状态,这样就能保证自适应算法随滤波精度的提高而更准确地估计运动模型,采用最优的时间配准算法。
此外,由于本文算法只需在常用时间配准算法基础上增加两个门限判断逻辑以完成机动检测过程,因此增加的计算量耗时可以忽略。
4 结束语
实际上,分布式结构下各传感器的机动跟踪滤波模型与真实目标的匹配度直接影响后续时间配准精度,当匹配度较高时,卡尔曼预测法的误差较小;当匹配度降低时采用线性或非线性的拟合算法比卡尔曼预测法能够达到更好的配准精度,例如本文中所描述的匀速运动和变加速运动状态下分别使用线性最小二乘拟合和二次多项式最小二乘拟合的配准精度更高。因此,本文提出基于机动检测自适应实时时间配准算法,融合中心根据航迹数据检测目标运动模型的变化,相应采用不同的时间配准算法,能够有效地降低时间配准误差。仿真结果表明,该算法性能优于现有算法,具有良好的工程应用价值。
[1]田明辉,方青,任清安.机载ESM与雷达航迹融合仿真系统研究[J].雷达科学与技术,2012,10(1):64-70.TIAN Ming-hui,FANG Qing,REN Qing-an.Simulation of Track Fusion of Airborne ESM and Radar[J].Radar Science and Technology,2012,10(1):64-70.(in Chinese)
[2]李学永,周俊.实时时间配准仿真研究[J].电子工程师,2007,33(11):1-4.
[3]李莉.时间配准在多传感器数据处理中的应用[J].仪器仪表用户,2011,18(3):65-66.
[4]黄春燕,满君丰.基于曲线拟合的多传感器时间对准算法研究[J].湖南工业大学学报,2012,26(4):72-75.
[5]袁赣南,袁克非,张红伟,等.基于分段重叠的时间配准方法[J].传感器与微系统,2012,31(8):48-51.
[6]施立涛.多传感器信息融合中的时间配准技术研究[D].长沙:国防科技大学,2010.
[7]杨稳竞.组网雷达时空对准研究[D].长沙:国防科技大学,2011.
[8]刘万全,徐世友,陈曾平.基于运动模型估计的分布式实时时间配准算法[J].现代雷达,2013,35(1):41-45.
[9]何友,修建娟,张晶炜,等.雷达数据处理及应用(第2版)[M].北京:电子工业出版社,2009.
[10]徐士良.数值分析与算法[M].北京:机械工业出版社,2006.
