单薄壁空心矩形墩连续刚构桥非线性稳定研究
2014-03-13刘大鹏
刘大鹏
(河北远洲工程咨询有限公司 河北石家庄 050035)
单薄壁空心矩形墩连续刚构桥非线性稳定研究
刘大鹏
(河北远洲工程咨询有限公司 河北石家庄 050035)
以一典型单薄壁空心矩形墩连续刚构桥——王家坝大桥施工监控项目为依托,以稳定理论为基础,利用ANSYS软件建立单薄壁空心矩形墩最高墩裸墩施工阶段模型、最大悬臂施工阶段模型和成桥阶段模型,并采用不同类型单元进行模拟,分析对比各施工阶段下的稳定特征值和非线性极限荷载,总结非线性对连续刚构桥稳定的影响规律,可为施工与设计提供参考。
非线性 稳定 特征值 极限荷载
随着交通事业的迅猛发展,为了穿越深沟峡谷,我国修建了大量的高墩大跨连续刚构桥结构,由于该类桥梁墩高、跨大、轻且柔,所以施工过程中的非线性问题非常突出,特别是薄壁空心高墩的大量采用,导致施工过程中的安全问题日益突出。结构失稳是指结构在外力增加到某一量值时,稳定性平衡状态开始丧失,稍有扰动,结构变形迅速增大,使结构失去正常工作能力的现象。结构失稳一般可分为两类:第一类分支点失稳和第二类极值点失稳[1]。目前,对于简单荷载及规则的结构的第一类分支点失稳问题,主要采用解析法、能量法、差分法、渐进法等求解稳定临界力;而对于复杂荷载及变截面的第一类分支点失稳问题或第二类极值点失稳问题,主要采用有限元法。薄壁高墩连续刚构桥是典型的压弯构件,其稳定性问题属于第二类稳定。本文运用ANSYS软件,以王家坝大桥为例,对单薄壁空心矩形墩连续刚构桥施工过程的非线性稳定进行了研究。
1 王家坝大桥结构概述
王家坝大桥位于达陕高速公路D7标段,其下部结构为空心矩形钢筋混凝土桥墩,混凝土标号为C40,3#和4#主墩墩高分别为68和76 m,其立面示意图如图1所示。主梁结构为预应力混凝土单箱单室直腹板箱形梁,混凝土标号C55,跨中部梁高2.8 m,端部梁高6.5 m,箱梁高度由距墩中心3.0 m处按1.8次幂函数线形变化;底板宽6.5 m,箱梁顶板宽12.1 m,翼缘板悬臂长度2.8 m,桥面横坡变化由腹板高度调整;箱梁底板厚由距墩中心3.0 m处到合拢段处按1.8次幂函数线形由0.8 m变化至0.3 m。
2 高墩稳定问题分析的理论基础
基于能量变分原理的有限元方法可以较好地模拟各种形状的线形结构、平面结构和空间结构,以及杆件间的铰接和刚接特性,因此在高墩大跨桥梁的稳定分析中广泛采用。从力学角度来说,对结构的第二类稳定性进行分析,就是通过不断求解计入几何非线性和材料非线性的结构平衡方程,寻找结构极限荷载的过程。

图1 王家坝大桥立面示意图(单位:m)
由虚功原理建立的第二类稳定性问题的非线性有限元平衡方程为:

按式(2-1)可以求得在荷载{F}作用时的位移δ,如果荷载不断增加,则结构的位移增大。由于与荷载大小有关,因此这时结构的力与位移的关系不再是线性的,如果达到时,结构呈现随遇平衡,这就是所求的临界荷载点。

如λ足够大,使得结构达到随遇平衡状态,即当{δ}变为{δ}+{Δδ},则式(2-2)变为:

要同时满足式(2-2)(2-3)的条件是:

这就是计算稳定安全的特征方程式,如果方程有n阶,那么理论上存在n个特征值λ1λ2λ3......λn。但在实际工程问题中只有最小的特征值才有意义,这时的特征值为λmin,即为最小稳定特征值,λmin{F}即为临界荷载。
3 单薄壁空心矩形墩连续刚构桥非线性稳定分析
高墩施工过程中有三个工况需要引起特别关注,一个是高墩自体施工至墩顶时,高墩自体的稳定性问题,一个是施工到最大悬臂状态工况时的稳定问题,还有一个是全桥合龙以后成桥状态时的稳定问题,下面就选取最高墩为研究对象,对此三工况根据以上研究理论和ANSYS计算方法对其进行计算分析。
3.1 最高桥墩自体施工工况稳定分析
选取最高墩为研究对象是因为最高墩在施工过程中所承受的重力、横向风荷载和纵向风荷载、温度影响是所有桥墩中最大的。
为了比较各种单元之间计算结果的差异和验证计算结果的可靠性,分别选取梁单元、板壳单元与实体单元建立模型,对该桥最高桥墩自重作用下的线性屈曲特征值进行了计算。由于桥墩在施工过程中一直处于受压状态,为了简化模型,未考虑普通钢筋的作用,仅考虑自重作用,墩底采用固结约束,对于第一类线弹性稳定的计算,不需要考虑结构的材料非线性,因此结构的材料参数按表1来取值,其计算结果见表2。特征值屈曲分析属于线性分析,特征值临界失稳荷载的大小应为F=实际施加荷载×第一阶失稳特征值。

表1 线弹性稳定分析材料参数的选取

表2 最高桥墩自重下自体施工稳定屈曲特征值
相对理想的设计状态,连续刚构桥的薄壁空心桥墩由于上述因素的影响,实际上存在几何线形上的偏差,一般称为初始几何缺陷,这样在分析薄壁空心高墩时必须考虑几何非线性对其稳定性的影响。对于几何非线性的考虑只需用ANSYS中合适的单元进行模拟,并在求解过程中用nlgeom,on命令将大变形打开即可[2]。
混凝土材料的本构关系可采用多线性等向强化模型MISO、多线性随动强化模型MKIN模型等。本文采用多线性Mises随动强化屈服准则来考虑桥墩的材料非线性,以模拟混凝土达到极限压应变时的破坏条件。文中混凝土的材料非线性的定义通过混凝土的非线性应力—应变关系来实现,应力—应变关系采用了三种曲线[3-7]:Hognest应力—应变曲线(材料a)、多线性随动强化应力—应变曲线(材料b)、Sansz应力—应变曲线(材料c),如图2~图4所示。由于实际结构存在缺陷和材料非线性等原因,会使荷载还未达到理论的弹性屈曲荷载时结构就会发生失稳。

图2 Hognest应力—应变曲线图

图3 多线性随动强化应力—应变曲线图
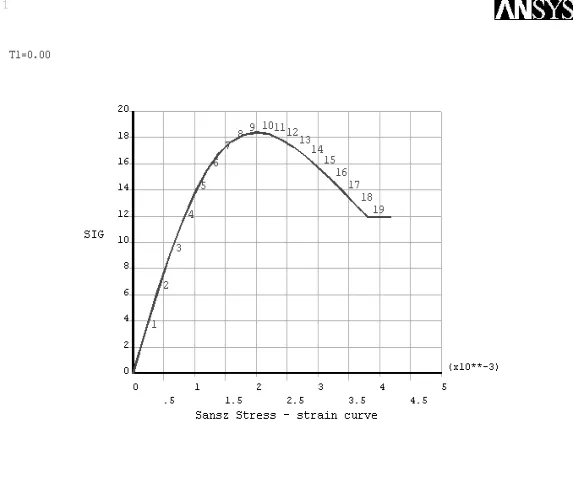
图4 Sansz应力—应变曲线图
目前常采用以下两种准则,来确定考虑材料非线性的稳定分析时的极限荷载[8]。一种是以结构构件边缘纤维应力达到屈服强度时的荷载作为极限荷载;另一种是以荷载—位移曲线上(荷载/位移)变化率发生突然降低的点作为极限荷载。本文采用后一种准则来确定极限荷载,极限荷载由ANSYS软件分析得出的荷载-位移曲线求得,曲线的最高拐点对应的就是极限载荷[9-12],其计算结果见表3、表4。

表3 最高桥墩自体施工稳定状态仅考虑几何非线性时的极限荷载
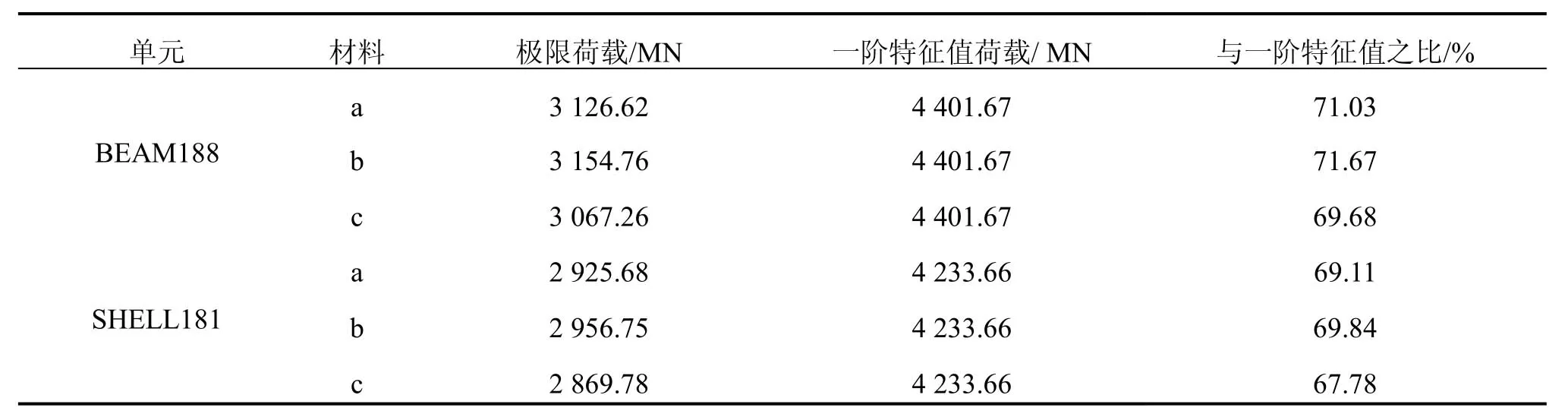
表4 最高桥墩施工自体稳定状态考虑双重非线性时的极限荷载
3.2 最高墩最大悬臂施工工况稳定分析
通过对最高桥墩自体施工工况分析得出的数据可以看出,各种单元的计算结果比较接近,因此计算过程是可靠的,且梁单元和壳单元建模方便,所以对最高墩最大悬臂状态稳定进行分析,仅用梁单元和壳单元进行了模拟。采用Sansz应力—应变曲线的塑性材料来考虑桥墩的材料非线性,其计算结果见表5、表6。

表5 最高墩最大悬臂状态下稳定屈曲特征值

表6 最高墩最大悬臂状态极限荷载
通过计算结果可以看出,梁单元和壳单元模型分析计算结果比较接近,几何非线性作用下极限荷载约是一阶特征值的78 %,双重非线性作用下极限荷载约是一阶特征值的60.83 %,这与自体稳定计算结果比较接近。由此可见,最高墩最大悬臂施工稳定的非线性影响主要来自高墩的几何非线性及墩身材料非线性的共同作用,单独考虑几何非线性时影响不大,考虑双重非线性时最高墩最大悬臂施工稳定影响比最高墩自体施工稳定影响明显增大。
3.3 成桥状态工况稳定分析
由以上两个工况的模型分析结果可以看出,BEAM188空间梁单元计算结果比较可靠,而且建立全桥模型比较方便,为简化计算,仅考虑自重作用,墩底采用固结约束,成桥状态梁单元模型如图5所示,其失稳特征值计算结果见表7,成桥状态一阶失稳如图6所示。
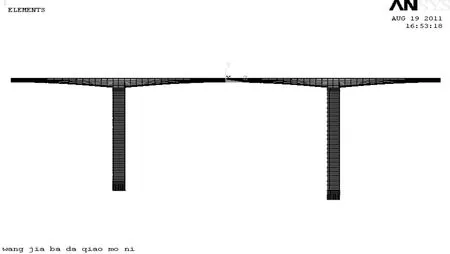
图5 成桥状态梁单元模型图

图6 成桥状态一阶失稳图

表7 成桥状态自重作用下稳定屈曲特征值
从桥梁成桥状态的特征值分析得出,一阶失稳为面外失稳,且一阶失稳的特征值比最高墩最大悬臂状态下稳定屈曲特征值大,因此最高墩最大悬臂状态施工为稳定的最不利工况,应加强对该施工状态的控制。成桥状态为保证桥梁不向面外失稳,可将左右幅桥墩横向连接,这样可以更好的利于稳定。由应力云图可以看出在成桥状态最大应力仍然在主梁悬臂根部断面,中跨合龙后合龙段应力会明显增大,比最高墩最大悬臂状态时大,说明中跨合龙后结构体系发生转换,将对全桥应力产生很大影响。
4 结论
从王家坝大桥高墩施工过程中三个工况的稳定分析,可以得出以下结论:
(1)对桥墩自体施工工况进行稳定分析得出的一阶屈曲特征值为100左右,最高墩最大悬臂状态工况进行稳定分析得出的一阶屈曲特征值为27左右,成桥状态工况下进行稳定分析得出的一阶屈曲特征值为34左右,可以分析出最高墩最大悬臂施工状态工况为施工中稳定最不利工况。从最高墩自体施工工况非线性稳定分析结果可以看出,采用Sansz应力—应变曲线来考虑墩身混凝土的材料非线性时,对稳定性的影响最大。
(2)总体上来说几何非线性对单薄壁空心矩形墩稳定性影响较小,双重非线性对单薄壁空心矩形墩稳定性影响较大,考虑双重非线性的最高墩最大悬臂施工状态屈曲荷载计算值仅有一阶特征值屈曲荷载的60 %,可见在高墩最大悬臂状态施工中对非线性行为影响应该重视。
(3)采用线弹性分析得到的是第一类稳定问题的解,只能得到屈曲荷载和相应的失稳模态,得出的屈曲荷载是第二类稳定分析的上限值,不能当作结构设计的依据。由于非线性分析的结果能够较好的反映桥梁高墩的屈曲后特性,可以考虑几何非线性、材料的非线性以及初始缺陷等因素的影响,计算结果更准确、更符合实际情况,可作为工程设计中的理论值。特别是最近设计的高墩大跨连续刚构桥上部结构越来越轻盈,截面越来越经济,在设计、施工验算校核中更应考虑非线性因素对稳定的影响。
[1]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2002
[2]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.10
[3]郭梅.高墩大跨连续刚构桥稳定性分析[J].西安公路交通大学学报,1999,19(3) :31~35
[4]武芳文,薛成风,赵雷.连续刚构桥梁悬臂施工线形控制分析[J].铁道工程学报,2006,Vol.94No.4P.29~33
[5]R W CLOUGH .The Finite Element Method in Plane Stress Analysis[J]. Proc.Znd ASME Conference of Electronic Computation,Pittsburgh,Pa,SePt.1960
[6]LI Li,PENG Yuanchen. Nonlinear Stability Analysis of Long-Span Continuous Rigid Frame Bridge with Thin-Wall High Pier[J]. Journal of China University of Geosciences,Vol.16,No.1, p.72 -78 ,March2005
[7]李开言,陈政清等.双肢薄壁高墩施工过程稳定性分析的快速算法[J].铁道学报.2004(5)
[8]郝超.大跨度钢斜拉桥施工阶段非线性结构行为研究[D].博士学位论文.成都:西南交通大学,2000
[9]MATTHEW J MOYER, MERVYN J. KOWALSKY. Influence of Tension Strain on Buckling of Reinforcement in Concrete Columns[J].ACI Structural Journal,2003,100(1):75~85
[10]潘家英,张国政,程庆国.大跨度桥梁极限承载力的几何与材料非线性耦合分析[J].土木工程学报,2000,33(1):5~8
(PAN Jiaying, ZHANG Guozheng, CHENG Qingguo.Geometrical and material nonlinear analysis for determining ultimate load capacity of long-span bridges[J].China Civil Engineering Journal,2000,33(1):5~8.in Chinese)
[11] HOSHIKUMA J, KAWASHIMA K, NAGAYA K,et a1. Stress—strain model for confined concrete in bridge piers[J], J Structural Eng, 1997, 123(5):624~633
[12] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress—strain model for confined concrete[J]. J Structural Eng, 1988, 114(8):1 804~1 826
Study on Nonlinear Stability of Continuous Rigid Frame Bridge with Single Thin Wall Hollow Piers
LIU Da-peng
(Hebei Yuanzhou Engineering Consulting Co., Ltd. Shijiazhuang Hebei 050035 China)
Based on the monitoring of the construction project of a typical continuous rigid frame bridge with single thin wall hollow piers----Wang Jia Ba Bridge and theory of stability, the model of the highest pier of the thin-wall hollow rectangular piers in the construction phase, the model of the largest cantilever bridge in the construction and POSTCS phases are established using ANSYS software and are all simulated by adopting different units. The eigenvalue of stability and nonlinear limit load under various construction stages are analyzed and compared and the influence law of the nonlinear on continuous rigid frame bridge construction process is summarized, which can offer information and reference for the construction and design of the same type of bridge.
nonlinear stability eigenvalue limit load
A
1673-1816(2014)04-0001-06
2014-10-16
刘大鹏(1982-),男,湖北天门人,硕士,研究方向高墩大跨桥梁施工过程及荷载试验方面研究。
