Markov随机场与Gaussian曲线在 MR图像分割中的应用

杨 涛

（云南机电职业技术学院,云南 昆明 650203）

Markov随机场与Gaussian曲线在 MR图像分割中的应用

杨 涛

（云南机电职业技术学院,云南 昆明 650203）

针对扫描的人脑组织 MR图像边缘分辨率低、模糊性大的特点，本文提出了一种基于模糊 Markov随机场和Gaussian曲线相结合的 MR图像最佳阈值分割方法。该方法通过对图像的像素邻域属性的统计将模糊论引入其中，建立模糊 Markov随机场，并利用Gaussian曲线对二维直方图最佳一维投影进行拟合，确定出图像中各脑组织的二维阈值点，在二维直方图上实现对脑组织的分割。通过实验表明，本算法能够有效提高脑组织的分辨率，对噪声的鲁棒性、结果区域的连通性相对于一维Otsu和二维Otsu算法都有了很大的提高。

模糊 Markov随机场；二维直方图；投影；Gaussian曲线；阈值

1．引言

脑部核磁共振(magnetic resonance， MR)图像在成像、传送和显示的过程中，会引入大量的噪声，使图像质量下降，整体变得模糊、失真，甚至导致各种脑组织无法正确分辨[1]。为了提高各脑组织在图像中的分辨率，抑制噪声的影响，改善 MR图像的显示效果，对 MR图像进行恢复对于神经病理学的研究和临床诊断具有十分重要的意义， MR图像中脑组织分割的准确性、自适应性和处理速度在一定程度上影响着具体的临床应用。

在众多图像分割方法中，阈值法因为其计算简单、算法效率高、速度快等优点被广泛采用。在以往提出的大部分阈值分割方法都是基于一维直方图，最常见的一种方法是一维最大类间方差法[2](一维Otsu)。然而，由于人脑内部组织复杂，有很多的纹理结构和相互粘连的组织区域，而且 MR图像本身模糊，如果只依据一维直方图分布来确定各类的分割阈值，不仅抗噪能力弱，而且区域的一致性和完整性也较差，图像很难实现精确分割。刘键庄和栗文清提出了二维直方图上的Otsu分割方法[3]，由于图像二维直方图考虑了灰度空间分布，较一维直方图更能清晰地反映图像的聚类信息，因此，此方法在一定程度上克服了一维Otsu抗噪声弱的缺陷，但在区域连通性和抗模糊方面仍然不够理想。基于此，本文将模糊集、 Markov随机场模型聚类、二维直方图和Gaussian曲线模型的思想结合起来，提出了一种脑部 MR图像多阈值分割算法，用于解决多目标的脑部 MR图像的准确分割。

2．模糊 Markov随机场

为了采用一个最优（能量最小）的 Markov随机场来实现对图像准确聚类，本文从原始图像随机场Y中以最大后验概率（ MAP）寻求真实的区域标记随机场X，即P(X=x|Y=y)最大的状态，即=arg根据Hamersley Clifford定理， Markov先验能量场P(X)可以用Gaussian分布来描述，即式(1)，似然函数P(Y|X)根据图像的一般特征可以认为是服从(v，σ2)的正态模型，由贝叶斯规则， Markov后验能量场可用式(2)描述。

从式（1）、（2）中不难看出，要建立一个恰当的 Markov随机场关键的问题是如何定义恰当的势函数。本文考虑到脑部组织结构的复杂性和 MR图像本身模糊的缺陷，采用了模糊理论中隶属度函数μ来表示势函数，即式（5）。同时，为了更好地体现图像像素同类值呈Gaussian分布的规律，文中根据正态分布的3σ规则来定义图像像素的隶属度函数，并将其引入到区域标记随机场X中，如式（4），使得图像中的每一个像素在被标记时不但具有了区域标识，而且还根据式（3）被赋予了隶属于该区域的隶属度，为实现 MR图像的模糊聚类奠定了基础。

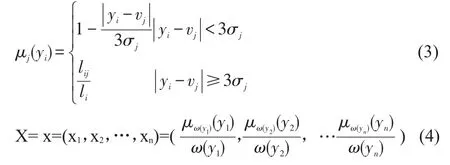
式（3）中，lij表示在以像素i定义的邻域中隶属于于区域j的像素点数，li表示像素i所定义的邻域中像素点数。式（4）中，ω(yi)i∈S为像素i的区域隶属标识，ω(yi)=1，2，3，4。

3．二维直方图最佳投影和Gaussian曲线模型

图像的二维直方图所建立的二维灰度特征空间不仅融合了图像像素的灰度的分布，还考虑了像素之间的邻域空间的信息，由此，利用二维直方图对 MR图像进行多阈值分割的方法既能较清楚地划分目标组织和背景，又能有效消除噪声。但在二维直方图上要确定最佳阈值，相对于一维直方图的方法较复杂，运算量按指数增长，耗时长，难以实用[4-5]。本文利用了文献[4]中二维直方图最佳一维投影方法对脑部 MR图像所形成的二维直方图进行了一维投影，并通过建立与分类数n相同的Gaussian曲线模型逼近该一维投影直方图，获得相邻两Gaussian曲线模型的交点n-1个，即作为各脑部组织的投影阈值点。

3．1 二维直方图的最佳一维投影

李立源等在文献[4]中提出了一种最佳一维投影定理，即：对于二维直方图，当坐标系旋转角度θ满足tanθ=（其中，d为像素正方形的邻域窗口宽度，一般取奇数）时，其在一维轴上的投影为最佳一维投影[4]。依此定理，本文将二维直方图上表示灰度值及邻域平均灰度值点(i，j)据公式eij=-i·sinθ+j·cosθ把二维直方图上任意点(i，j)的发生频率数hij在一维轴上的eij处叠加形成二维直方图的一维投影直方图。（如图1c、g所示）

投影后的一维直方图不可避免地存在伪峰及毛刺，本文为了不影响后续Gaussian曲线模型的建立，将投影直方图的任意一点的统计值用其临近点的均值进行平滑。

3．2 建立Gaussian曲线的数学模型

从Gaussian曲线不难看出，建立模型主要是确定模型包含的灰度级范围，本文利用模糊 Markov随机场聚类法所确定的类均值vm和相邻两类的均值vm-1，vm+1来确定建立该类组织Gaussian曲线的灰度级中心和范围，然后根据Gaussian分布的公式建立Gaussian高斯曲线：

上述公式中pk=g(k)/sum，其中g(k)表示投影直方图k点上的统计数值；sum表示两类的均值vm-1和vm+1范围内所有点数和。v'm表示类均值vm在投影直方图的投影。(如图1d、h所示)

图1 三幅 MR脑核部分图像二维直方图最佳一维投影的高斯拟合

4．本文算法实施及实验结果分析

4．1 算法实施

本文以采用真实的 MR颅脑图像作为研究对象，并使用 C++高级语言程序实现该算法。算法如下：

(1)根据图像像素灰度特点，用传统的K-means方法初步获取各类别的统计均值和方差并将类均值设为该类初始的聚类中心。

(2)根据式(3)求得像素的隶属度，并在标记场中对像素的类别以予标记。

(4)按照“最大后验概率准则”使用式（2）进行条件迭代，确定每个像素的类别：

(5)采用像素的新隶属度，结合质心公式得到新的类均值和方差，即式（8）、（9）：

(7)统计MR图像的像素灰度值及邻域信息得到二维直方图；

(8)遵循二维直方图最佳一维投影原理，将二维直方图进行一维投影，并对其平滑处理；

(9)根据式（6）建立Gaussian曲线模型，获得相邻两Gaussian曲线模型的交点n-1个，即作为各脑部组织的投影阈值点，t1，t2，…tc-1；

(10)根据tm=-i·sinθ+j·cosθ，m=1，2…c-1将n-1个交点映射回二维直方图，确定出分割阈值线，按照以下式（10）完成对 MR图像的分割，即：

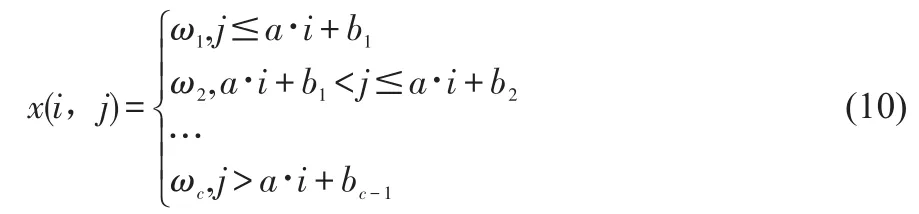
4．2 实验的结果分析

采用本文提出的模糊 Markov随机场与二维直方图Gaussian曲线多阈值新方法对两幅真实的 MR图像进行了实验分析，并于本文提到的一维Otsu方法和二维Otsu方法进行了比较。如图2所示。

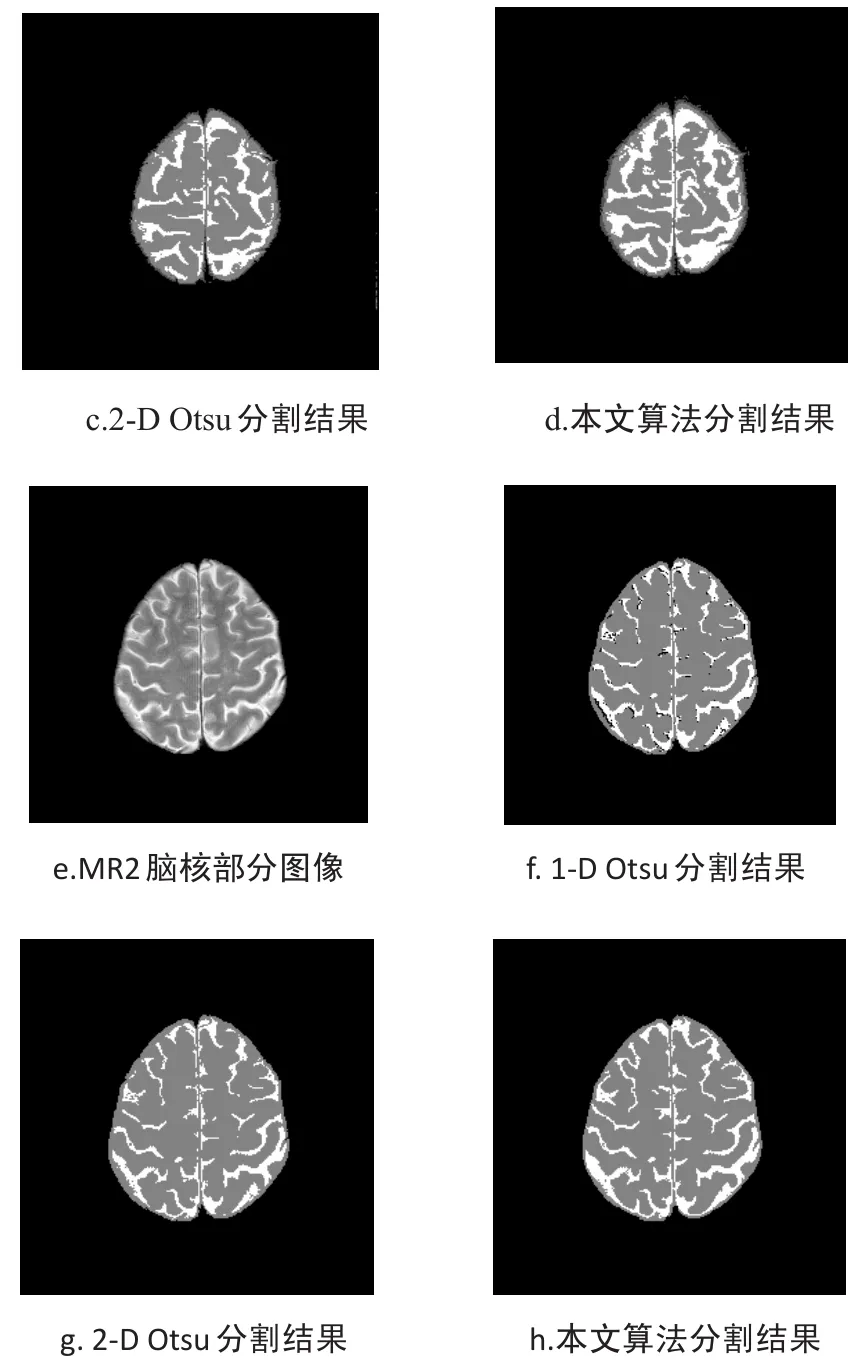
图2 三幅 MR脑核部分图像分割结果

从分割结果可以看出，一维Otsu算法抗模糊和抗噪能力差，分割结果中含有大量的噪声点，分割后的区域一致性较差；二维Otsu算法虽然在抗模糊和噪声方面相对于一维Otsu算法有了很大的提高，但是，在区域连通性方面仍然有所欠缺。本文算法克服以上两种算法的缺陷，不仅抗模糊和噪声能力强，而且算法分散点少，即区域连通性较好。

鉴于本文主要研究如何将 MR图像中各脑组织有效地区分开，所以评价分割方法是否有效的指标之一就是图像像素是否按其灰度特征正确归类，因此，本文采用以下两个体现分类有效性的指标（划分系数和划分熵）对目标图像进行定量分析。两个指标函数如下：

式中当μij＝0时，有μijlog(μij)＝0。对于有效的算法应当根据图像像素特征对其能正确归类，而且在不同类别边缘应有明显的区分度，用划分系数表征时其值越大越好，而用划分熵表征时则反之。

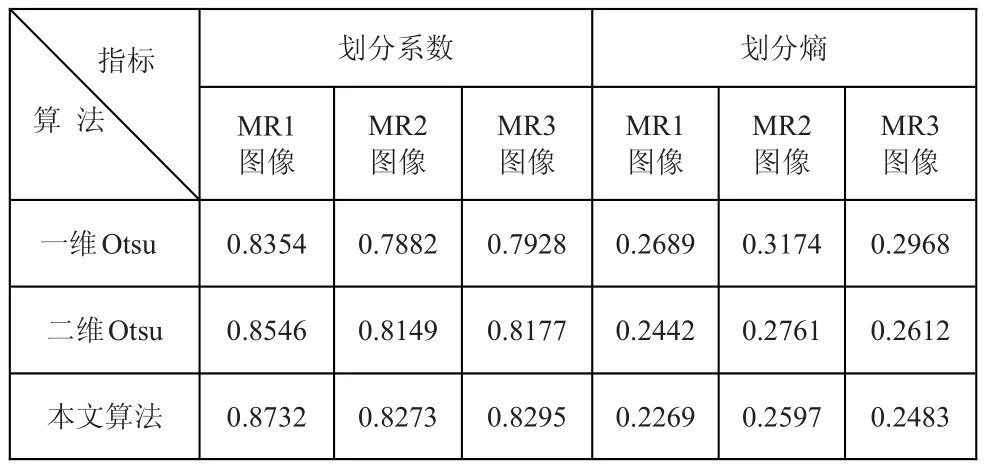
表1 不同算法的划分系数和划分熵指标

从表1所示的划分系数和划分熵两指标的定量分析来看，本文算法明显优于一维Otsu算法和二维Otsu算法，它的分类有效性更高、混乱性更小。

5．结论

本文充分融合了模糊集和 Markov随机场模型，并引入二维直方图的最佳一维投影和Gaussian曲线拟合方法，提出了模糊 Markov随机场与二维直方图Gaussian曲线的最佳阈值分割方法。实验证明，该方法相对于一维Otsu算法和二维Otsu算法在抗模糊和噪声的能力方面有所提高，并在一定程度上克服了分割区域连通性差的问题，从而得到良好的 MR图像分割结果。

[1]杨涛．基于统计方法的核磁共振人脑图像的分割及三维数据的分析[D]．昆明：昆明理工大学硕士论文，2011,4．

[2]罗军辉，冯平．MATLAB 7．0在图像中的应用[M]．北京：机械工业出版社，2005．

[3]刘键庄，栗文清．灰度图像的二维Otsu自动阈值分割法[J]．自动化学报，1993,19：101-105．

[4]李立源，龚坚，陈维南．基于二维灰度直方图最佳一维投影的图像分割方法[J]．自动化学报：1996,22：315-322．

[5]田杰，曾建潮．基于QPSO的二维模糊最大熵图像阈值分割方法[J]．计算机工程,2009，35(3)：230-232．

Application of Markov Random Field and Gaussian Curve in MR Image Segmentation

Yang Tao
(Yunnan Vocational College of Mechanical and Electrical Technology,Kunming 650203,Yunnan)

For the low resolution and the large fuzziness of the organizational structure of human brain at the edge of MR image scanned,a better threshold MR image segmentation method based on fuzzy Markov random field clustering and Gaussian curves is proposed.In the algorithm,fuzzy theory is introduced into the statistics of the pixel neighborhood attributes,and fuzzy Markov random field is set up.Then the optimum one-dimensional projection histogram of two-dimensional histogram is fit with Gaussian curves and found segmentation points in each class region.Finally,image segmentation is realized in the two-dimensional histogram.Experiments show that the proposed algorithm can improve the effective resolution of the various brain tissues,and it is better than the one-dimensional Otsu method and two-dimensional Otsu method in the noise robustness and partition connectivity of the result.

fuzzy Markov random;two-dimensional histogram;projection;Gaussian curve;threshold value

杨涛，男，云南昆明人，硕士，助教，研究方向：嵌入式,应用电子。