中考数学成绩好不好，思想方法见分晓

胡金柱

在中学阶段，数学思想是以渗透的方式，出现于各种知识模块的各个知识点中的.因此，学习、掌握、应用数学思想，必须以理解、掌握基础知识和基本技能为前提，否则数学思想就成了无源之水、无本之木.若能把掌握好的数学思想方法灵活地运用到中考中，中考数学成绩自然会高人一等.下面例析初中数学常见数学思想方法在中考中的应用，希望对同学们有所启迪.

一、函数与方程思想

函数思想就是用运动、变化的观点分析和研究现实中的数量关系，通过问题所提供的数量特征及关系建立函数关系式，然后运用有关的函数知识解决问题.如果问题中的变量关系可以用解析式表示出来，则可把关系式看作一个方程，通过对方程的分析使问题获解.

所谓方程的思想，就是突出研究已知量与未知量之间的等量关系，通过设未知数、列方程或方程组，解方程或方程组等步骤，达到求值目的的解题思路和策略.它是解决各类计算问题的基本思想，是运算能力的基础.函数与方程思想是中学数学中最常用、最重要的数学思想之一.

例1 （山西卷）下图是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案，则第n个图案中阴影小三角形的个数是 .

解析 由图可知：第一个图案有阴影小三角形2个，第二个图案有阴影小三角形6个，第三个图案有阴影小三角形10个……则形成数对（1，2），（2，6），（3，10）……

设阴影小三角形的个数与图案的次序之间的关系为y=kx+b，

将（1，2），（2，6）代入，得k+b=22k+b=6，解得k=4b=-2.

∴ y=4x-2.检验知（3，10）也符合此表达式.

∴阴影小三角形的个数与图案的次序之间的关系为y=4x-2. ∴当x=n时，y=4n-2.

故第n个图案中阴影小三角形的个数是4n-2.

二、分类讨论思想

在数学中，我们常常需要根据研究对象性质的差异，分各种不同情况予以讨论.这种分类讨论的方法是一种重要的数学思想方法，同时也是一种解题策略.

引起分类讨论的因素较多，归纳起来主要有以下几个方面：

（1）由数学概念、性质、定理、公式的限制条件引起的讨论；

（2）由数学变形所需要的限制条件所引起的分类讨论；

（3）由于图形的不确定性引起的讨论；

（4）由于题目含有字母而引起的讨论.

分类的原则有：①分类中的每一部分是相互独立的；②一次分类按一个标准；③分类讨论应逐级进行.

例2 （湖北襄阳卷）如果关于x的一元二次方程kx2-■x+1=0有两个不相等的实数根，那么k的取值范围是（ ）

A.k<■ B.k<■且k≠0 C.-■≤k<■ D.-■≤k<■且k≠0

解析 由题意，根据一元二次方程二次项系数不为0的定义知： k≠0；

根据二次根式被开方数非负数的条件得：2k+1≥0；

根据方程有两个不相等的实数根，得■=2k+1-4k>0.

三者联立，解得-■≤k<■且k≠0. 故选D.

三、数形结合思想

数形结合思想是数学中重要的思想方法.所谓数形结合就是根据数学问题的题设和结论之间的内在联系，既分析其数量关系，又揭示其几何意义，使数量关系和几何图形巧妙地结合起来，并充分地利用这种结合，探求解决问题的思路，使问题得以解决的思想方法.运用这一数学思想解题，要熟练掌握一些概念和运算的几何意义及常见图形中的代数特征.

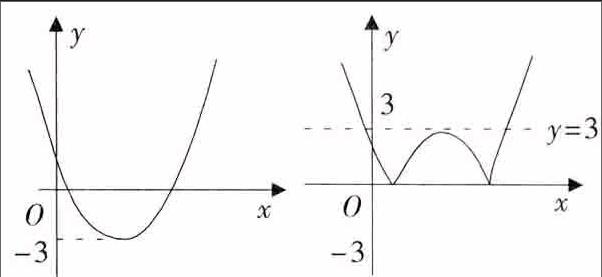
例3 （甘肃兰州卷）二次函数y=ax2+bx+c（a≠0）的图象如图1所示，若|ax2+bx+c|=k（k≠0）有两个不相等的实数根，则k的取值范围是（ ）

A. k<-3 B. k>-3 C. k<3 D. k>3

解析 根据题意得：y=|ax2+bx+c|的图象如图2，

所以，若|ax2+bx+c|=k（k≠0）有两个不相等的实数根，则k>3.故选D.

点评 本题考查了二次函数的图象，解题的关键是根据题意画出y=|ax2+bx+c|的图象，然后根据图象得出k的取值范围.

四、整体思想

整体思想，就是在研究和解决有关数学问题时，通过研究问题的整体形式、整体结构、整体特征，从而对问题进行整体处理的解题方法.从整体上去认识问题、思考问题，常常能化繁为简、变难为易. 整体思想的主要表现形式有：整体代入、整体加减、整体代换、整体联想、整体补形、整体改造等等.

在初中数学中的数与式、方程与不等式、函数与图象、几何与图形等方面，整体思想都有很好的应用，因此，每年的中考中涌现了许多别具创意、独特新颖的涉及整体思想的问题，尤其在考查高层次思维能力和创新意识方面具有独特的作用.

例4 （湖南娄底卷）如图3，正方形MNEF的四个顶点在直径为4的大圆上，小圆与正方形各边都相切，AB与CD是大圆的直径，AB⊥CD，CD⊥MN，则图中阴影部分的面积是（ ）

A. 4π B. 3π C. 2π D. π

解析 ∵ AB⊥CD，CD⊥MN，

∴ 根据轴对称的性质，阴影部分的面积恰好为正方形MNEF外接圆面积的■.

∵ 正方形MNEF的四个顶点在直径为4的大圆上， ∴ S阴影=■π×（■）2=π.故选D.

五、转化与化归思想

所谓转化与化归思想，就是将待解决的问题和未解决的问题，采取某种策略，转化归结为一个已经能解决的问题，或者归结为一个熟知的具有确定解决方法和程序的问题，最终求得原问题的解.

转化与化归思想的原则：

（1）熟悉已知化原则：将陌生的问题转化为熟悉的问题，将未知的问题转化为已知的问题，以便于我们运用熟知的知识、经验和技巧来解决.

（2）简单化原则：将复杂问题转化为简单问题，通过简单问题的解决思路和方法，获得对复杂问题的解答启示和思路以达到解决复杂问题的目的.

（3）具体原则：化归方向应由抽象到具体.

（4）和谐统一性原则：转化问题的条件或结论，使其表现形式更符合数与形内部所表示的和谐统一的形式；或者转化命题，使其推演有利于运用某种数学方法或符合人们的思维规律.

（5）正难则反的原则：当问题正面讨论遇到困难时，应想到问题的反面；或问题的正面较复杂时，其反面一般是简单的；设法从问题的反面去探求，使问题获得解决.

例5 （山东泰安卷）如图4，AB∥CD，E、F分别为AC、BD的中点，若AB=5，CD=3，则EF的长是（ ）

A.4 B.3 C.2 D.1

解析 连接DE并延长交AB于H，

∵ CD∥AB， ∴ ∠C=∠A，∠CDE=∠AHE.

∵ E是AC中点， ∴ DE=EH. ∴ △DCE≌△HAE（AAS）， ∴ DE=HE，DC=AH.

∵ F是BD中点， ∴ EF是△DHB的中位线， ∴ EF=BH. ∴ BH=AB-AH=AB-DC=2，

∴ EF=1. 故选D.

点评 作辅助线：连接DE并延长交AB于H，把EF变换成△DHB的中位线，使问题易于解决，体现了由未知——已知、综合——单一的化归.

例6 （山西卷）如图5，一次函数y=（m-1）x-3的图象分别与x轴、y轴的负半轴相交于A、B，则m的取值范围是（ ）

A. m>1 B. m<1 C. m<0 D. m>0

解析 根据一次函数图象与系数的关系， ∵函数图象经过二、三、四象限， ∴ m-1<0，解得m<1. 故选B.

点评 根据一次函数图象与系数的关系，把m的取值范围问题转化为求解不等式，体现了由抽象——具体的化归.（编辑 孙世奇）