低轨道量子卫星通信时分交换方案及性能分析*

杨 光，聂 敏，江 帆

（西安邮电大学通信与信息工程学院 西安 710121）

1 引言

量子通信基于海森堡不确定性原理和量子态不可克隆定理，能够实现不可破译与窃听的安全保密通信。近年来随着全球信息安全问题的加剧，量子通信愈加成为人们关注的科学领域。由于光子在外层空间传播时几乎没有损耗，基于卫星构建量子通信网成为实现广域范围安全保密通信的一个新思路。同步卫星通信系统由于其轨道高度达数万公里，时延长、退相干影响大，短期内不具备同步量子卫星通信的实用化条件。而低轨道卫星系统轨道高度较低，星地链路时延相对较小，是实现卫星量子通信的一种较为可行的选择。当前，有关量子卫星通信的研究主要围绕星地量子密钥分发问题[1～3]，参考文献[4]研究了星地密钥传送的单光子捕获理论，参考文献[5]研究了背景光对星地量子密钥分发误码率的影响。参考文献[6]研究低轨道卫星量子信道切换等。然而，量子卫星通信网是一个多用户系统，如何解决多个用户的接入与量子信息交换是十分关键的问题[7～9]。时分多址与交换是在经典通信网中常用的技术，但其进行时分交换的关键部件是信息存储器。受限于量子存储器的技术发展状况，经典时分交换并不能直接应用于量子信息交换。参考文献[10]提出了一种陆地量子时分交换系统，但并不适用于多波束、高时延的星地量子通信场合。

本文提出了一种多波束低轨道量子卫星时分交换方法，各个波束上的多个用户可在不同的时隙接入星地量子信道并经量子时分交换机将信息传送至目的用户。为克服量子卫星系统的时延对吞吐量的影响，本文提出了基于量子信道字的传送与交换方法，有助于降低单量子比特平均传输时延，提高系统吞吐量。

2 低轨道量子卫星时分交换通信系统结构

2.1 系统总体结构

低轨道量子卫星时分交换通信系统结构如图1所示。为实现全球覆盖，该系统由M个轨道平面组成，每个轨道平面内包含N颗卫星。每颗卫星具备4条星际量子链路，分别连接至同轨道内的两颗相邻卫星及相邻轨道面上的两颗卫星。在每颗卫星上，均配备一个多波束时分量子交换机，对地面的量子通信终端进行覆盖。在每个波束的覆盖区，为各个量子发送终端分配不同的通信时隙。此外，本系统需要经典卫星信道的辅助，以完成卫星量子通信的终端位置管理、连接控制、切换控制等。

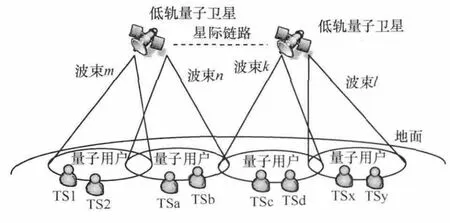
图1 低轨道量子卫星通信系统结构

2.2 时分卫星量子交换机结构

时分量子卫星交换机以多波束方式工作，其结构如图2所示。整个时分量子交换机由信令控制模块、时钟同步模块、量子处理与交换模块、外部接口4部分构成。

图2 时分卫星量子交换机结构

信令控制模块负责处理通信信令并执行内部控制逻辑，根据终端位置指配量子波束或星际链路，并分配量子通信时隙。信令的收发通过经典卫星信道进行。时钟同步模块通过外部同步接口产生时钟同步信号，并提供给交换机的其他模块使用。在本系统中，所有的量子卫星交换机、量子通信终端都必须保持全网同步。具体的同步技术采用经典的卫星通信网同步方式。量子处理与交换模块包括纠缠对分发控制模块、EPR纠缠源、Bell基测量部件、幺正变换门、光开关阵列等。该模块的工作受量子连接状态表及时钟同步模块的控制，在指定的时隙产生EPR纠缠对，并对相应的光子进行Bell基测量和幺正变换等，从而建立纠缠交换通道。外部接口主要包括星地多波束时分量子链路接口、星际时分量子链路接口、经典卫星信道接口、时钟同步接口等。在星地多波束时分量子链路接口上，交换机在指定时隙通过各个纠缠光子发送器向不同波束覆盖区发射纠缠光子，每个发射望远镜采用不同的倾角。地面量子通信终端在指定时隙采用偏振追踪方式探测所在波束的光子。

2.3 量子信道字

在量子交换机的每个波束上，均提供N个通信时隙。每个时隙传送和交换的基本量子信息单元为一个量子信道字，它由L个量子比特组成。由于星地链路及星际链路的距离较长，无论是在纠缠光子的分发还是在经典信道上传递Bell基测量结果，都需要经历毫秒级的时延，这种时延对量子通信的吞吐量具有决定性影响。以星地间的纠缠光子分发为例，假设星地间的光子传输时延为τSE，制备一对EPR纠缠光子对的时间为τEP，分发1个光子，采用参考文献[10]方法需要的传输时间为（τSE+τEP），而采用本文方法分发一个光子需要的平均传输时间为（τEP+τSE/L）。由于τEP的取值为纳秒级，因此基于信道字的方法将单量子比特平均传送时延约降低为原来的1/L，有利于提高卫星量子通信系统的吞吐量。

3 时分量子通信过程

低轨卫星系统中，用户的通信过程与其所处位置有密切关系，假设每个通信用户都能通过GPS等获取自己的当前位置。用户间的量子通信过程主要有3种方式:同一卫星、同一波束下用户间的通信；同一卫星、不同波束下用户间的通信；不同卫星下用户间的通信。前两种通信过程类似，下面主要说明后两种通信过程。

3.1 同一卫星、不同波束下用户间的通信

在进行量子通信之前，首先需要经由经典信令信道执行呼叫建立过程，如图3所示。

图3 量子卫星呼叫建立过程

主叫用户1的终端首先在经典信道上搜索卫星导频信息，当搜索到导频信号最强的卫星时，在信令信道上向卫星发起呼叫请求，该请求中携带主、被叫地址以及主叫位置等。卫星交换机收到该请求后，对被叫用户2地址进行分析，发现该被叫当前位于自己的覆盖范围下并空闲，于是向用户2发送呼叫请求信令，若用户2接收该呼叫，则返回呼叫确认信令，该消息中携带用户2的位置信息。卫星交换机根据用户1、用户2所在的位置，为用户1指配量子波束1，为用户2指配波束2；并根据当前的量子信道忙闲表分配波束1、波束2上的一个空闲时隙，假定为时隙i，i作为本次通信时隙。接下来，交换机向用户1和用户2发送信道指配信令，说明本次通信使用的波束和时隙，若用户同意该分配，则返回信道确认信令，接下来卫星交换机将本次通信连接的信道及波束分配情况写入量子连接状态表，量子通信开始。

当时隙i到来时，通信过程按以下步骤进行。

（1）EPR纠缠源依次产生L对处于Bell态的纠缠光子，这些量子态如式（1）所示:

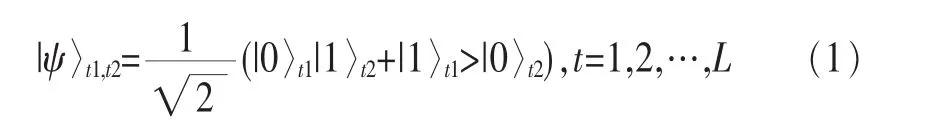
（2）纠缠分发部件依次将光子t1送至纠缠光子发送器1，从而在波束1上向用户1发送光子t1；同理纠缠光子发送器2在波束2上向用户2发送光子t2。

（3）用户1和用户2分别依次探测到光子t1、t2。

（4）用户 1 产生 L 个待发送光子 t0，t=1，2，…，L，其量子态为:

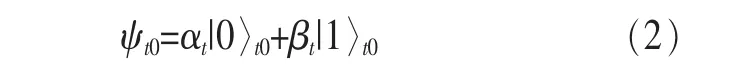
此时，光子 t1、t2及量子态 ψt0的总量子态可以表示为:

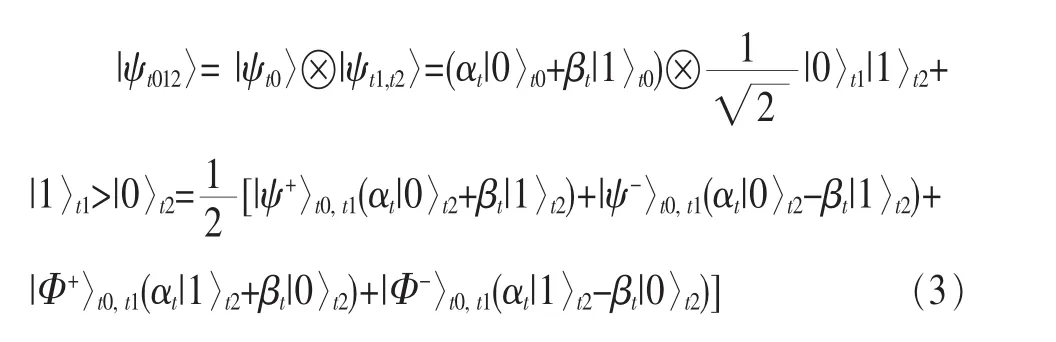
（5）用户1依次对光子t0和t1进行Bell基测量，测量结果将等概率得到4个Bell基中的一个。则用户2获得的光子t2必处在和光子t0的原始状态直接相关的一个量子态中。

（6）接下来，用户1通过经典信道通知用户2这L个测量结果，然后用户2对光子t2做适当的幺正变换，见表1。便可获取光子 t0 的信息（αt,βt）。

至此，在时隙i上，用户1将L个量子态ψt0传送至用户2。若要实现用户间的双向通信，同理可分配另一时隙j，在该时隙上，用户2将待发送量子态发送给用户1。

3.2 不同卫星下用户间的通信

当主叫用户1处于卫星1覆盖范围下，被叫用户2处于卫星2的覆盖范围下，经过与第3.1节类似的过程，卫星1分析出用户2位于卫星2。于是向卫星2发出呼叫请求信令，卫星2向用户2发呼叫请求信令……经过与第3.1节类似的信令过程，假设为用户1分配卫星1下的波束1，为用户2分配卫星2下的波束2，本次通信分配时隙k，则在时隙k到来时，量子通信过程为:

表1 量子隐形传态幺正变换

（1）卫星1上的纠缠源依次产生L对Bell态纠缠光子:

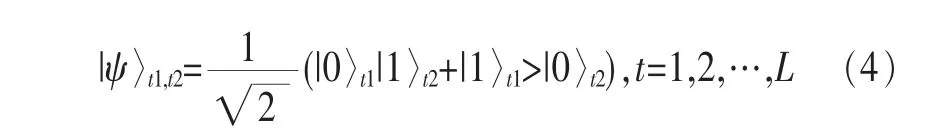
（2）卫星2上的纠缠源依次产生L对Bell态纠缠光子:

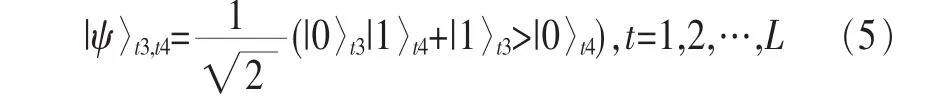
（3）根据量子连接状态表，卫星1上的纠缠分发部件在延迟时间D后依次把光子t1发送至纠缠光子发送器1，D取决于卫星1计算的纠缠交换时延；卫星1把光子t2发送至星际纠缠光子发送器E1。

（4）卫星2探测到光子t2，并把自己产生的光子t3和光子t2送入Bell基测量模块进行测量。在测量前，光子t1、t2、t3、t4 的总量子态为:

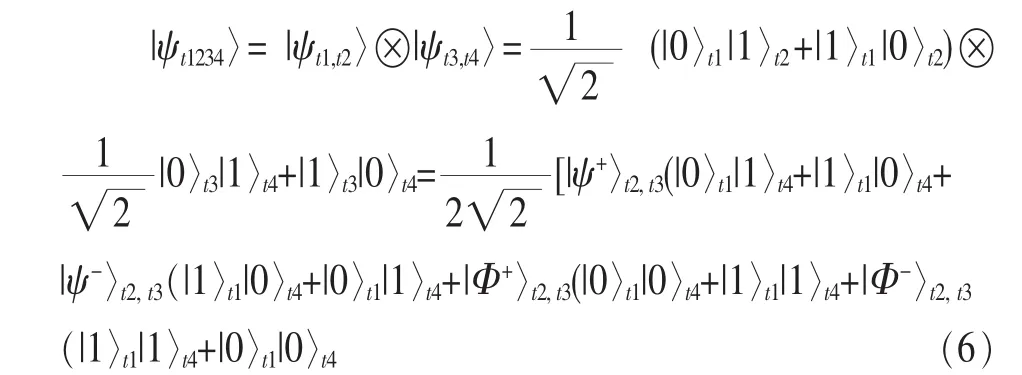
测量后，光子t1和t4将根据测量结果等概率地塌缩到4个量子态之一。

（5）为使 t1、t4 共享的纠缠态仍为|ψ+〉t1,t4=(|0〉t1|1〉t4+|1〉t1|0〉t4，卫星2需根据测量结果对光子t4进行幺正变换，幺正变换见表2。

（6）卫星2将光子t4发送至纠缠光子发送器2，在该时隙，用户2探测到光子t4。至此用户1与用户2之间的纠缠交换通道建立，用户1可以采用与前面同样的隐形传态方式向用户2发送量子态ψt0，这里不再赘述。

表2 纠缠交换幺正变换

4 分析与仿真

4.1 系统的吞吐量

在本系统中，传送一个量子信道字需要的总时间可以表示为:

Te表示在主叫用户和被叫用户间建立纠缠信道的平均时间；Tm表示主叫用户进行Bell基测量的平均时间；Tt表示主叫用户通过经典信道将测量结果传给被叫的平均传送时间；Tu表示被叫根据测量结果进行幺正变换恢复量子比特的平均时间。设一个量子信道字长为L个量子比特，一次通信中需要跨越的平均卫星个数为S，则:

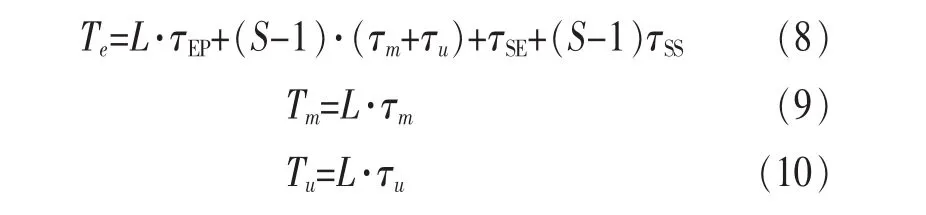
其中，τEP为制备一对EPR纠缠对的平均时间，τSE为从卫星向地面传送纠缠光子的平均时间，τSS为在一段卫星链路上传送纠缠光子的平均时间，τm为进行一次Bell测量的平均时间，τu为进行一次幺正变换的平均时间。设一个波束上的时隙数为N，则一个波束周期的总时间长度为:

在量子信息的传输过程中，由于信道噪声及量子设备等的影响，不可避免地造成量子信息的传送差错。假设系统中的量子比特误码率为Pe，则对一个时隙上的通信用户，其成功传送量子信道字的最大速率为:

对一个时隙上的通信用户，其成功传送的平均最大量子比特率，即吞吐量为:

采用MATLAB对系统的吞吐量Rqb进行仿真，仿真参数取典型值 τEP=1 ns，τm=2 ns，τu=3 ns，τSE=1 ms，τSS=3 ms,Tt=2 ms，S=4。

图4给出了当Pe取0.05时，在不同时隙数N下，每个波束上单个时隙用户的最大量子比特率随信道字长的变化曲线。可见随着时隙数的增大，单时隙用户最大量子比特率降低，这是由于系统总吞吐量一定，时隙数越多，用户数越多，分配到单用户的吞吐量越少。在时隙数一定的情况下，单用户的最大量子比特率随信道字长度的增加而增加，这是由于量子信道字越长，单个量子比特的平均传输时延越小，量子比特传输率越高。但当量子信道字增加到一定长度后，量子信道字的成功传送概率下降占据主导因素，因而平均量子比特率开始下降。图5给出了在N=8时，不同误码率下，单时隙用户吞吐量随信道字长的变化曲线。可见，在一定的误码率下，都存在一个最佳信道字长，使得吞吐量最大。随着误码率的增加，最佳信道字长减小。

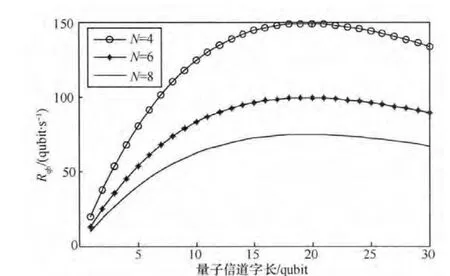
图4 单个时隙上的用户吞吐量

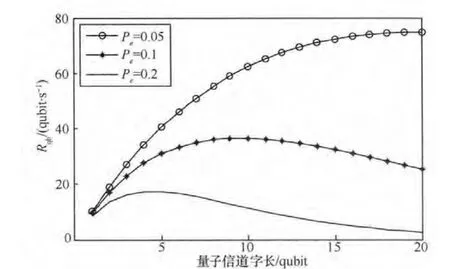
图5 误码率对最佳信道字长的影响

4.2 系统的呼损率

卫星量子时分交换系统采用固定时隙交换方式，当所有的时隙都已被占用，则不再接收新的用户呼叫，因此本系统属于呼损制系统，采用排队论进行分析，该系统符合M/M/m/m模型。假设一个卫星交换机提供X个波束，每个波束上N个时隙，则m=N·X。系统的呼损率即为m个时隙都占用的概率为:

这里λ表示用户业务的稳态平均到达速率，μ代表稳态平均服务速率。图6给出了每波束的不同时隙个数下，单波束上呼损率随λ/μ值的变化曲线。可见随着λ/μ值的增加，系统呼损率增大；当时隙个数越多，系统提供的信道越多，呼损率降低。但同时，由于时隙数的增加，将降低单用户的最大量子比特传输率，因此在实际的网络设计中应根据呼损率及量子比特率的要求进行综合考虑。

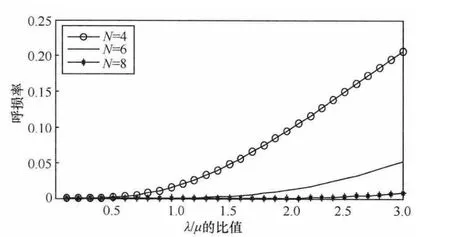
图6 系统的呼损率

4.3 与已有量子时分交换方案的对比

在已有的量子时分交换方案中[10]，在每个时隙进行交换和传送的信息为一个量子比特。而在本文的方案中，在每个时隙进行交换和传送的信息为一个量子信道字，该量子信道字由L个量子比特组成。在低轨道卫星量子通信系统中，较大的星地、星际链路时延对系统的吞吐量起着决定性的影响作用。若将参考文献[10]的方案直接应用于低轨道量子卫星通信系统中，则在每个量子比特的交换传送过程中，都需要经历沿途所有星地、星际链路段的总时延，对系统的吞吐量产生不利的影响。而应用本文方案则能够将沿途星地、星际链路段的总时延分摊到L个量子比特，从而提高系统的吞吐量。图7给出了在低轨道量子卫星系统中应用参考文献[10]的方案及本文方案的单时隙吞吐量对比。从图7中可以看出，在其他参数相同的情况下，本文方案的单时隙吞吐量明显大于参考文献[10]的方案，且随着信道字长的增加，吞吐量有所上升。但根据第4.1节的分析结论，信道字长并不能任意增加，在一定的量子误码率条件下，存在一个最佳字长使得吞吐量最大。

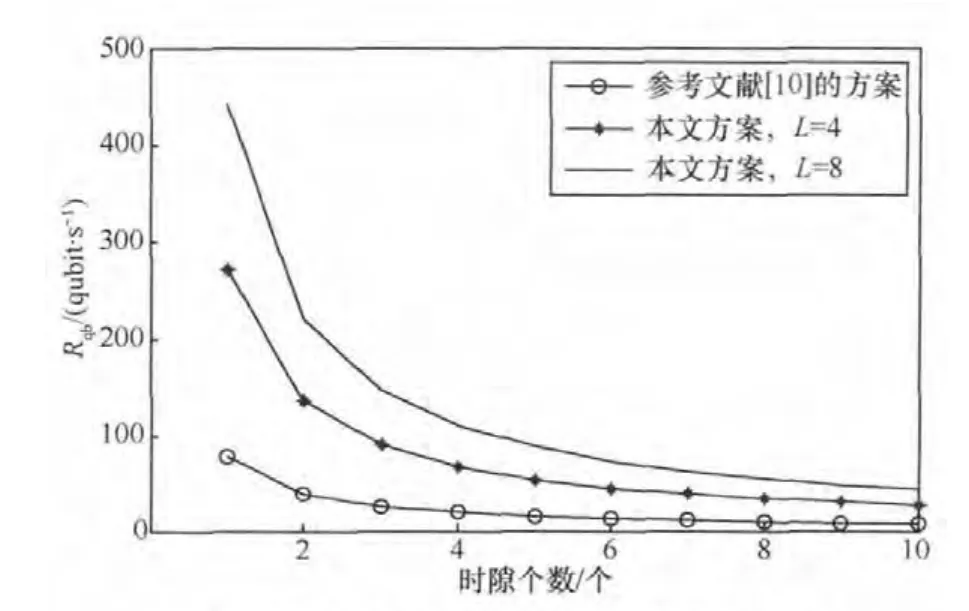
图7 本文方案与已有方案的单时隙吞吐量对比

5 结束语

随着量子通信重要性的不断突显，全球各科技强国都在着手进行卫星量子通信网的研究开发。本文提出的时分量子交换方法有助于在现有条件下解决低轨道卫星通信系统的多用户通信问题，并有助于在较大的时延条件下提高系统量子信息传输吞吐量。在系统的具体设计中，时隙个数及信道字长的选取可根据系统的误码性能、用户业务速率需求及系统呼损指标要求来确定。

1 崔明路，王治强，刘薇.一种星地量子密钥通信仿真平台.中国科学院研究生院学报,2011,28(2)

2 罗海龙，陈砚圃，裴昌幸等.星地量子密钥分发链路持续时间分析与仿真.量子光子学报,2009,15(1)

3 史春燕，钟红恩.星-地量子密钥分配误码率及成码量分析仿真.计算机仿真,2012,29(11)

4 张光宇，于思源，马晶.星地量子密钥分配中单光子捕获理论分析.光电工程,2006,33(3)

5 张光宇，于思源，马晶等.背景光对星地量子密钥分配量子误码率的影响.光电工程,2007,34(2)

6 王志，聂敏.低轨道量子卫星通信星上交换算法及仿真.光子学报,2012,41(9)

7 郭忠文,马鸿洋.多用户网络量子密码术的改进.计算机工程与设计,2006,27(20)

8 Skander A,Abderraouf M,Malek B,et al.Approach of large satellites networks communications based on quantum transmissions.Proceedings of2011 6th IEEE Conference on Industrial Electronics and Applications,Beijing,China,2011

9 刘晓慧，聂敏.基于ASON的量子通信网络构建和量子交换机设计.电信科学,2011(4)

10 Liu X H,Pei C X,Nie M.The time division multi-channel communication model and the correlative protocol based on quantum time division multi-channel communication.Chinese Physics Letter,2010,27(12)