基于有限域逆映射的轻量级加密SOPT-S盒构造与研究*
2014-03-12樊兆龙徐启建徐勇军
樊兆龙 ,徐启建 ,徐勇军 ,王 飞
(1.中国人民解放军理工大学 南京 210007;2.中国电子设备系统工程公司研究所 北京 100141;3.中国科学院计算技术研究所 北京 100080)
1 引言
随着普适计算的深入发展,人们可以随时随地、快速透明地获得所需的数字化服务,由于各种各样的信息数据均为人们共享,信息的安全问题也越来越复杂。如战场中的军事传感网,节点在感知并获得战场实时信息的同时需对其加密以确保安全,并且考虑到传感器节点能量小、计算能力低的特点,解决这一问题需要设计一个既能在能量及计算能力受限的传感器节点上实施,又具有顽健性的轻量级加密算法。S盒作为分组密码结构中唯一的非线性组件对于加密算法的顽健性有着重要的作用[1]。虽然现在存在许多安全性能较高的S盒,如AES中的S盒可以抵抗差分攻击、线性攻击等几乎所有的攻击,但由于其8×8的S盒需要1000 GE(gate equivalent),其大规模不适合能量受限的无线传感网节点等设备[2]。另外,6×6(300 GE)S盒以及DES中6×4(120 GE)S盒也不符合轻量级需求。参考文献[3]介绍了一种超轻量级加密算法PRESENT,该算法的非线性层采用4×4 S盒实现混乱特性,每个S盒只需28 GE,满足小规模、低消耗的设计要求。参考文献[4]随后提出了一种新的算法LED(light encryption device),其中S盒的设计与PRESENT相同。参考文献[5]中根据Feistel型密码构造出LBlock密码,该密码非线性由8个不同的4×4 S盒并置而成。虽然4×4规模的S盒符合节点对于轻量级的要求,但是其加密算法的安全性也随之降低,例如在参考文献[6]的轻量级加密算法 KLEIN中,使用了 4×4对合S盒,即S盒的输入输出成对出现,虽然降低了解码的硬件要求但是其密码学特性中的差分均匀度以及雪崩效应随之降低。因此,设计一个规模小但安全性高的S盒用于传感器加密成为国内外研究的首要问题。
虽然算法抗攻击性能不完全由S盒决定,但是在轻量级加密算法S盒中,依然是重要的一部分,小规模S盒若没有较好的性能,整个算法的安全性也将受到影响。本文基于有限域GF(24)上的逆映射构造出一类次最优(suboptimal)4×4 S盒,首先通过求解GF(24)上不可约多项式对应的逆元,再经过一个仿射变换从而得出一系列S盒,最后根据设计要求筛选得出性能最佳的S盒。该算法首次将AES中S盒的构造方法用于轻量级S盒的构造,将其密码学特性进行分析并与典型的轻量级加密算法PRESENT中S盒进行对比发现,该S盒的雪崩概率以及代数次数均优于PRESENT的S盒,抵抗差分攻击的能力也强于后者,具有良好的密码学特性,可以用于轻量级加密非线性层的设计中,为算法后续模块的设计奠定良好的基础。
2 预备知识
S盒概念首次出现在Lucifer算法中并随之广泛应用于DES、AES等许多密码算法[7],其设计要求是构造一个性能优良的S盒首先需要考虑的问题。
由于S盒的密码学特性可用多输出布尔函数来描述[8],所以通过对多输出布尔函数的分析来具体研究轻量级S盒(4×4)的设计思路。衡量其密码学指标主要包括以下几项。
(1)非线性度
令 S(x)=(f1(x),…,fn(x)):GF(2)n→GF(2)n是一个多输出函数,则S(x)非线性度为:
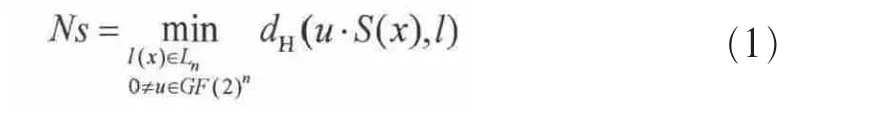
其中,Ln为全体n元线性仿射函数集,dH(u·S(x),l)表示函数S(x)与l(x)之间的汉明距离。非线性度决定了S盒抵抗线性密码分析的能力,非线性度越高,则抵抗线性攻击的能力越强。当S(x)达到上界2n-1- 时,称为Bent函数,即非线性最佳。
(2)差分均匀性
n×n S盒差分均匀度可表示为:
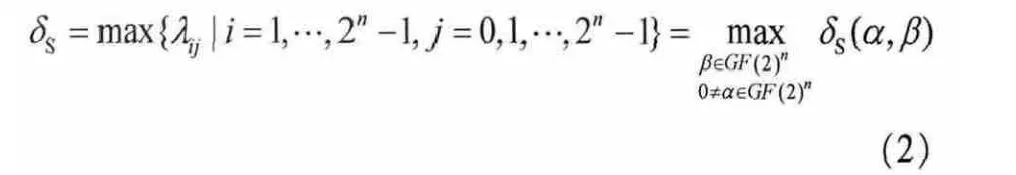
其中,δS(α,β)=|{x=GF(2)n:S(x堠α)+S(x)=β}|。差分均匀性是用来衡量该密码抗击差分密码分析能力的指标,由差分分布表来反映。差分分布表反映了输入差分与输出差分分布情况,分布越均匀,即差分传播概率最大值越小,S盒抵抗差分攻击的能力越强,最佳为满足差分2-一致性S盒。
(3)雪崩效应
指S盒输出任一比特与输入比特之间的关系,衡量输入改变对输出改变的随机性,即当输入有1 bit改变时,有一半输出比特改变时则满足雪崩效应,而当每个输出改变的概率(雪崩概率)为1/2时,满足严格雪崩准则(SAC)[8]。
(4)代数次数及项数分布
代数次数用来衡量S盒的代数非线性程度,代数次数越高,项数越高,复杂度就越高,因此越难用线性表达式逼近。当S盒输入为n时,最佳的代数次数值为n-1。
3 SOPT-S盒的构造
根据上面提出的设计原则,下面将基于有限域上的逆映射来构造4×4的SOPT-S盒,这类S盒具有良好的密码学特性并且无陷门[1]。同时,许多大规模的S盒(AES)依靠此类数学函数方法来实现,这为轻量级S盒的构造提供了理论基础。
3.1 SOPT-S盒构造方法
基于有限域上的逆映射的构造主要分为两个可逆步骤。首先,将状态字与GF(24)中的元素一一对应并在GF(24)上求出各状态字的逆元。然后,根据上步求出的结果再通过一个仿射变换从而构造出4×4 S盒,该仿射变换可表示为:

其中,X-1为第一步的输出,m(x)表示有限域 GF(24)上的任意4次多项式,μ(x)在保证与m(x)互素的原则下任意选择,v(x)为仿射常量,保证变换过程中不存在不动点与反不动点。
根据近世代数相关知识可知伽罗瓦域GF(24)上仅存在3个不可约多项式,分别为:x4+x+1、x4+x3+1和x4+x3+x2+x+1。分别求出其各自对应状态字[0123456789 A B C D E F]的逆元:

其中,括号里使用状态字的16进制来表示即可得到(X-1)的值。
μ(x)可通过一个矩阵U来表示,由于S盒为4×4 S盒,因此令 U=[U3U2U1U0],则:

关于仿射常量v(x)=[v3v2v1v0],则保证变换过程不存在不动点和反不动点,即S(x)=x和S(x)=。
最后可得出S盒的输出如下:
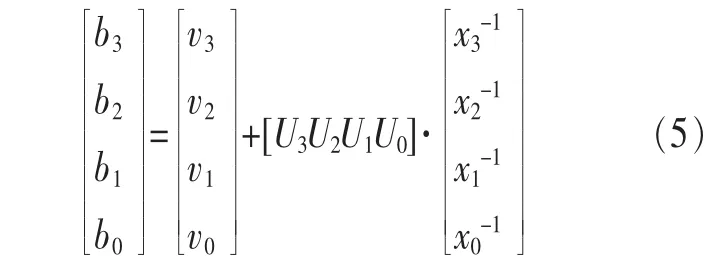
通过对伽罗瓦域GF(24)上3个不可约多项式下的m(x)、μ(x)以及v(x)进行穷举测试可得出4000多个S盒,其中除去不包含不动点以及反不动点的S盒,剩余约有600多个,然而并不是这600多个S盒的密码学性能都可以达到最佳,通过以下分析可以得到若干组{m(x)、μ(x)、v(x)},以生成最佳S盒。
由于消除不动点与反不动点时引入的仿射常量v(x)不影响S盒的密码学特性,所以由式(8)可知决定S盒性能的参数为 U 矩阵,即 m(x)和 μ(x),m(x)表示有限域 GF(24)上的任意4次多项式,μ(x)与m(x)互素,由此可知m(x)的选择至关重要,m(x)可取 x4+1、x4+x、x4+x2、x4+x3、x4+x2+1、x4+x2+x、x4+x3+x2、x4+x3+1、x4+x3+x、x4+x3+x2+1、x4+x3+x2+x、x4+x2+x+1、x4+x3+x+1、x4+x3+x2+x+1。
定义1 在矩阵U中,若每行每列非零个数均相同,则称为均匀U矩阵。
对于上述多项式m(x),可将其分为不可约多项式、只含一个因子的多项式以及含多个因子的多项式。当m(x)为不可约多项式时,μ(x)可取任何一个多项式均与其互素。根据式(3)可知不存在一个μ(x)使得U矩阵为均匀矩阵。当m(x)为只含一个因子的多项式时,很容易得出该因子为 x+1,对应的 m(x)为 x4+1,此时,当取 m(x)与 μ(x)互素的多项式时,得到的U矩阵均为均匀矩阵。当m(x)为含有多个因子的多项式时,与μ(x)生成的U矩阵不存在均匀阵。
证明 当时m(x)=x4+1,由式(3)可知,Ui多项式可表示

所以m=x4+1时,可以发现如下规律:不同μ(x)生成的均匀矩阵与各状态字的逆元相乘之后得到的矩阵中每一行均为任意3个各不相同的状态字的模2和。而m(x)取其他多项式时并不存在该规律(此处略去证明部分),由此为寻找最优S盒提供了途径。通过对该m(x)以及所有与之互素的μ(x)进行穷举分析,构造出了雪崩效应以及代数次数最佳的S盒。
3.2 SOPT-S盒构造过程
(1)以不可约多项式为例进行S盒的构造。
取m(x)=x4+1,这时,与m(x)互素的多项式μ(x)分别为:

通过计算,仿射常量v(x)可取:v(x)=x2+x+1和v(x)=x,即 v(x)=[0111]和 v(x)=[0010]。现以 m(x)=x4+1、μ(x)=x2+x+1、v(x)=x2+x+1为例进行上述仿射变换可得:

根据式(6)求得S盒,见表1。
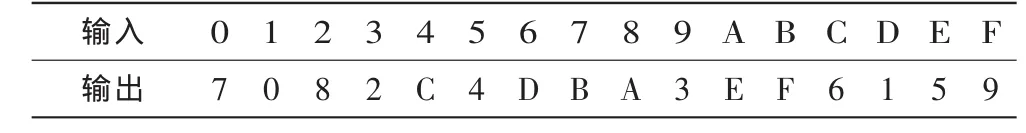
表1 SOPT-S盒
当然以上只是选择所有的{m(x)、μ(x)、v(x)}对中的一例进行 S 盒的构造,以下列出上述所有的{m(x)、μ(x)、v(x)}对以生成最佳S盒(包括上文已构造)。

(2)当不可约多项式取剩余两个多项式时,虽然一些密码学特性像非线性度以及差分均匀度与上述不可约多项式相同,然而对于雪崩概率以及代数次数并不能达到最佳,不能构成性能最佳的S盒,因此不做深究。
4 SOPT-S盒密码学性能
结合第1节给出的轻量级S盒设计准则以及第2节构造出的SOPT-S盒,本节将在对其密码学性能进行详细分析的同时,与现有典型的轻量级加密算法PRESENT非线性层中所使用的S盒进行对比,其中包括非线性度、差分均匀性和差分分布表、雪崩效应和雪崩概率、代数次数。
4.1 非线性度对比
非线性度决定了密码算法抵抗线性分析的能力,根据第1节中对于非线性的描述以及参考文献[9,10]的研究可知,假设 F(x):GF(2)n→GF(2)n,则非线性度为:
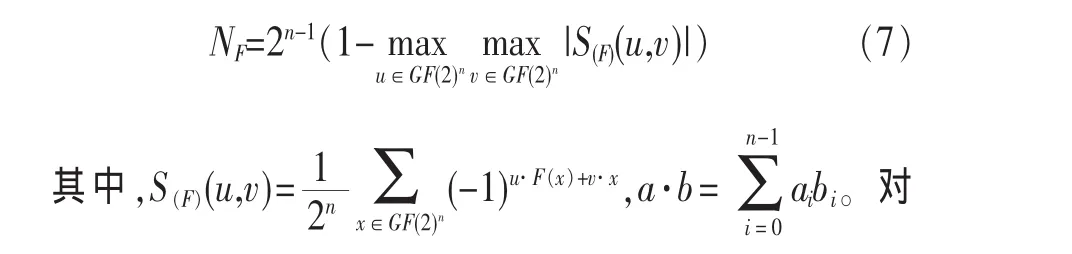
PRESENT中的S盒以及SOPT-S盒的非线性度进行求解可得如下结果:

其中,非线性度上界为 。结果表明,SOPT-S盒与PRESENT-S盒均具有较好的非线性度。
4.2 差分均匀性对比
较小的差分均匀度δ是S盒抗击差分密码分析的必要条件。由于差分均匀度可用差分分布表来反映,在此计算出了SOPT-S盒的差分分布,见表2。
其中,Δ(x)表示输入差分,Δ(y)表示输出差分,Δ代表了差分特征值,表1、表2均反映了当输入差分取0~F时对应的输出差分分别取0~F的个数,即差分特征数。
通过对表2进行分析可以看出:SOPT-S盒差分分布中每一行(除Δ(x)=0行)最高差分输出个数为4,满足上文提到的差分4-一致性,并且每行均有7个差分输出Δ(y)非0,同时第一列不包含非0元素,分布均匀。PRESENT-S盒虽然也满足差分4-一致性,但是大多数行分布都不均匀,存在包含1个以上差分输出个数为4的行,导致每行含0个数过多。其中第4行(Δ(x)=1)以及最后一行(Δ(x)=F)差分输出非零的个数仅为4个,非0个数最少。此外,当wt(ΔI)=wt(ΔO)=1时,差分输出的个数全部为 0,所以容易受到差分攻击。参考文献[11]对于其S盒的分析中同样可以看出,虽然满足其构造条件可以提高雪崩效应,但是并不能有效地抵抗差分攻击,因为当输入输出汉明距离等于1时,差分分布表中对应项为0,所以使得差分分布不均匀,导致了有差分攻击的可能性。总之,SOPT-S盒在差分均匀性这一指标上优于PRESENT-S盒,可以更好地抵抗差分攻击。
4.3 雪崩效应对比
S盒雪崩效应的优劣可以通过雪崩概率来度量,即改变输入的1 bit,输出比特改变的概率。当雪崩概率为1/2时,满足严格雪崩准则(SAC),此时雪崩效应为最理想[1]。表3和表4分别给出本文构造S盒的雪崩概率以及PRESENT-S盒的雪崩概率。

表2 SOPT-S盒差分分布
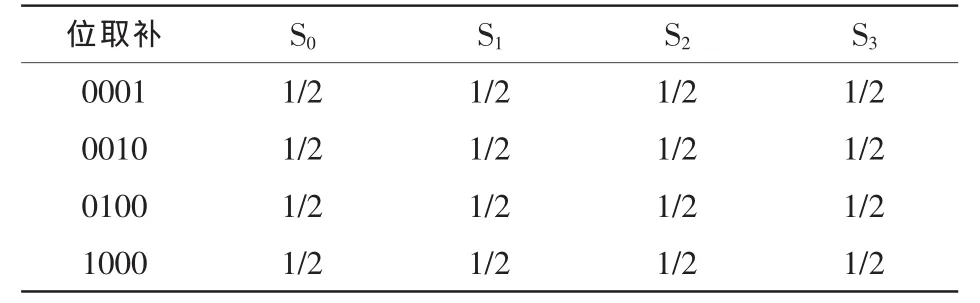
表3 SOPT-S盒雪崩概率
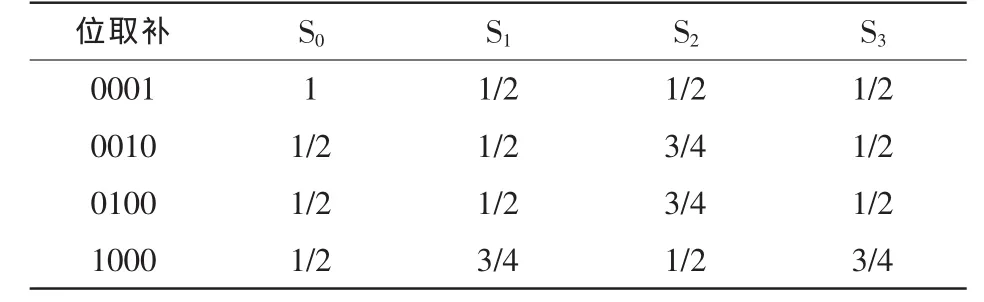
表4 PRESENT-S盒雪崩概率
其中,0001到1000分别表示从最低位到最高位进行取补运算,S1~S4表示S盒对应位改变的概率。
通过对比可以看出,SOPT-S盒雪崩概率值均为1/2,满足严格雪崩准则的条件。而PRESENT中S盒的雪崩概率值不全为1/2,其中包括了1、3/4以及1/2。由此表明,SOPT-S盒在雪崩效应指标上明显优于PRESENT的S盒,可以更快地将输入扩散到整个S盒中继而输出。
4.4 代数次数及项数对比
根据参考文献[10],4×4 S盒可以表示为有限域GF(2)上4 个布尔函数 :Sbox(x0,…,x3)=(f0(x0,…,x3),…,f3(x0,…,x3)),更进一步讲,S盒可由4个只含and和xor逻辑符号的布尔方程 fi(x0,…,x3)(0≤i≤3)表示:
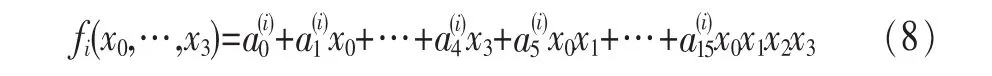
其中,aj(i)∈{0,1}是待确定的系数。据此可以确定SOPT-S盒布尔方程及其代数次数:
代数次数 D(f0)=3,D(f1)=3,D(f2)=3,D(f3)=3。
PRESENT-S盒布尔方程以及代数次数为:

代数次数 D(f0)=3,D(f1)=3,D(f2)=3,D(f3)=2。
将式(9)、式(10)两组方程进行对比整理,可得表 5。
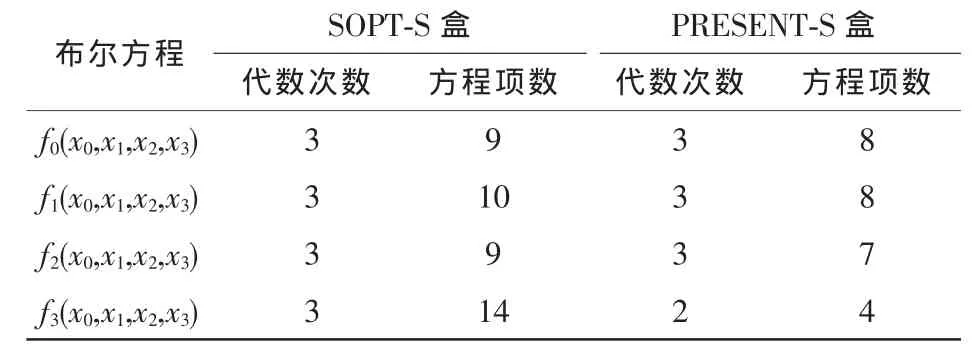
表5 结果对比
可以看出:SOPT-S盒4个布尔方程的代数次数全部达到了最佳 (n-1),同时方程项数越多,方程越复杂。而PRESENT-S盒代数次数没有全部达到最佳,最后一个布尔方程没有3次项,并且方程项数较少。因此,SOPT-S盒代数次数及项数分布指标也要优于PRESENT-S盒,可以更好地抵抗线性攻击和其他有关攻击。
将SOPT-S盒与PRESENT-S盒以上密码学特性进行总体上的对比,见表6。
表6从整体上反映出SOPT-S盒以及PRESENT-S盒的密码学性能,可以看出SOPT-S盒在雪崩效应以及代数次数两个指标上达到最佳值,非线性度和差分均匀度也保持与PRESENT-S盒性能相当,从而为轻量级加密算法的设计提供了有力的支撑,进而在战场上利用传感网节点能高效、快速地对获得的第一手信息进行加密,保证了信息不会暴露而是安全地传递。
4.5 与其他最优S盒对比
虽然现有的参考文献中提出了许多非线性最佳或者雪崩效率达到最佳即SAC的S盒,但只是在某一种密码学特性中表现最优,轻量级加密的设计需要对S盒的多个因素综合考虑,才能保证算法不被某一种攻击所攻破。参考文献[9]中提到,当函数的非线性为第1.1节介绍的Bent函数时,虽然非线性度达到最大,但是该函数并不是一个平衡函数 (不能构成S盒)并且代数次数不超过 D/2。参考文献[12]基于 APN(almost perfect nonlinear)函数构造了一种APN S盒,APN函数是有限域GF(24)上差分性质很好的非线性函数,APN S盒满足差分2-一致性,它在抵抗差分密码攻击以及线性密码攻击时最有效[13]。然而,APN S盒的构造要求函数必须为APN置换函数,满足这一条件同时执行变量n为偶数的APN函数并不存在。Dillon在参考文献[14]中构造出了分组密码执行变量为偶数(n=6)的APN多项式置换函数,满足差分2-一致性条件同时非线性达到了上界 ,但是n为6的S盒不满足构造轻量级S盒的要求。基于以上问题,本文构造的S盒在非线性度以及差分均匀度上取了折中,虽然未达到最佳值,但是在S盒的设计上遵循了轻量级的设计思路,同时在其他特性上达到了最佳,构造的次最优S盒很大程度上节省了硬件空间,适用于传感器节点的加密环境。
5 结束语
无线传感网的飞速发展带给传感器节点信息安全越来越大的冲击,传感器节点的信息加密已成为共同关注的话题,建立一个良好的信息加密体系对于城市管控、个人隐私、金融贸易,尤其在军事领域中有着重大的意义。然而节点在这种特殊的环境下完成加密任务对于加密算法的要求极为苛刻,不仅要保证S盒具有优良的密码学特性以满足算法的安全性和顽健性,还要保证S盒占有较小的硬件空间,从而实现算法的高效性。考虑到现有轻量级算法存在的一些问题,国家高技术研究发展计划(“863”计划)也将其作为研究的内容之一,可以说明研究轻量级加密算法S盒构造的必要性。本文基于有限域的逆映射构造出一类性能优良的S盒,并对其密码学性能进行了分析测试,与现在流行的加密算法PRESENT中的S盒相比,该S盒有着更好的密码学性能,其中雪崩效应以及代数次数均达到了最佳,同时在硬件实现方面,差分均匀度也与PRESENT-S盒占有的硬件开销相等,为轻量级加密算法中分组密码的非线性层设计提供了一种参考。对于未来轻量级S盒的研究,应着眼于寻找规模小,硬件(FPGA)实现简单,不仅可以很好地抵抗传统密码分析,而且对于扩展性的分析,如差分分析中的差分能量分析也具有较好的抵抗力。同时,从整个轻量级加密算法来看,对于非线性层与线性层二者的结合也是研究的一个方向。
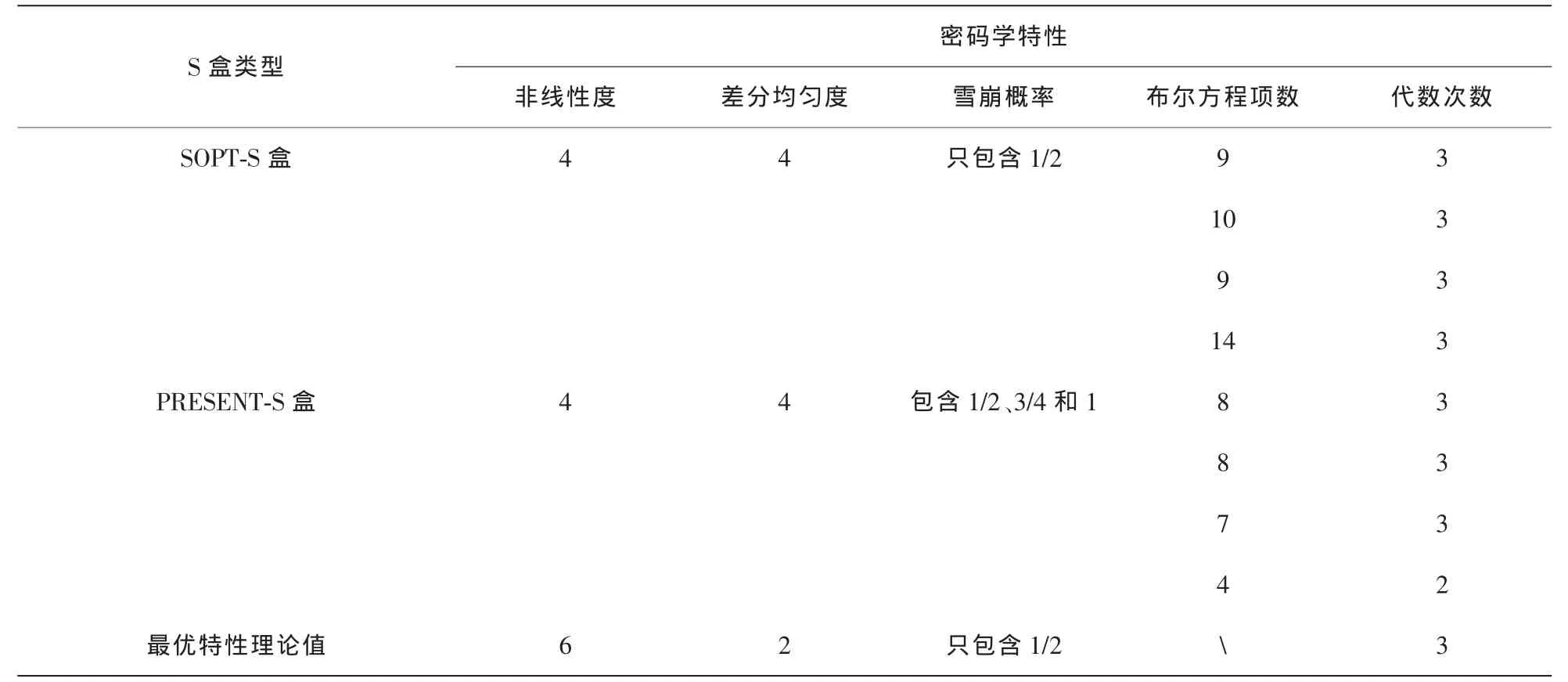
表6 整体性能对比
1 Feng D G,Wu W L.Design and Analysis of Block Cipher.Beijing:Tsinghua University Press,2000
2 Eisenbarth T,Paar C,Poschmann A,et al.A survey of lightweight-cryptography implementations.IEEE Circuits and Systems Society,2007(6)
3 Bogdanov A A,Knudsen L R,Leander G,et al.PRESENT:an ultra-lightweight block cipher.Proceedings of CHES 2007,Vienna,Austria,2007
4 Guo J,Peyrin T,Poschmann A,et al.The LED block cipher.Procedings of 13th International Workshop,Nara,Japan,2011:326~341
5 Wu W L,ZhangL.LBlock:alight weight block cipher.Proceedings of ACNS 2011,Nerja,Spain,2011:327~344
6 Gong Z,Nikova S,Law Y W.KLEIN:a new family of lightweight block ciphers.Proceedings ofRFIDSec 2011,Amherst,Massachusetts,USA,2011
7 Khoo K,Gong G.Highly nonlinear S-boxes with reduced bound on maximum correlation.Proceedings of IEEE International Symposium,Paris,France,2004
8 Qu L J,Tan Y,Tan C H,et al.Constructing differentially 4-uniform permutations over via the switching method.IEEE Transactions on Information Theory,2013(7)
9 Leander G,Poschmann A.On the classification of 4 bit S-boxes.Proceedings of Ari thmetic of Finite Fields,First International Workshop,WAIFI 2007,Madrid,Spain,2007
10 Gligoroski D,Elisabeth G M M.On deviations of the AES S-box when represented as vector valued boolean function.IJCSNS International Journal of Computer Science and Network Security,2007(4)
11 AlDabbagh S S M,Shaikhli I F T A.Security of PRESENT S-box.International Conference on Advanced Computer Science Applications and Technologies,Kuala Lumpur,Malaysia,2012
12 Fu M F.Research of block cipher S-box based on APN permutation.Network and Computer Security,2012(10)
13 Budaghyan L,Carlet C,Leander G.Constructing new APN functions from known ones.Finite Fields and Applications,2008(2)
14 Dillon J.APN Polynomials:An Update.International Conference Finite Fields and Their Applications,2009
