中心复合设计最优条件选取时四种方法的比较*

冯瑞梅王 婷戴 帅陈 益仇丽霞△

中心复合设计最优条件选取时四种方法的比较*

冯瑞梅1王 婷1戴 帅1陈 益2仇丽霞1△

目的比较三种传统优化方法和遗传算法基于中心复合设计的单目标优化时的特点。方法利用提高木聚糖酶产量的结果，分别用直接法、等高线法、最速上升法、遗传算法寻找最优结果，比较后得出结论。结果直接法、最速上升法、等高线法、遗传算法寻优的木聚糖酶含量分别为27.77UA/m l、23.93UA/m l、47.07UA/m l、51.04UA/m l。结论直接法可在其设计水平上较快找出结果，但不能保证局部或是全局达最优；在星点设计基础上的单目标寻优时等高线法的结果和遗传算法相当，等高线法可观察到部分因素对响应的影响大小，但存在局部最优和主观性较强的不足；最速上升法易陷入局部最优而忽略其他可能最优解。

中心复合设计 传统优化方法 遗传算法 最优试验条件

多因素、多水平的试验在实际应用中很常见，而常用的设计有析因设计、正交设计、均匀设计等，析因设计相对耗时、耗力，正交设计以牺牲高阶交互作用为代价降低了试验次数，均匀设计牺牲了整齐可比且在因子和水平多时效率高，而中心复合设计（central composite design，CCD），亦称为星点设计，是一种新型的试验设计方法，它具有试验次数少，试验精度高等特点，可以解决均匀设计和正交试验设计优化法的不足［1］。基于一定设计寻找最优试验条件是我们试验的目的，而采用的寻优方法包括传统寻优法（直接法、等高图法、最速上升或下降法等）和新近的解决全局优化问题的遗传算法等。本文将利用Design-Expert V8.0.6.1输出等高线图、SAS9.1RSREG过程及MATLAB2009a外挂SGSLAB工具箱单目标遗传算法程序寻找最优解，基于结果将对三种传统优化方法和遗传算法的效果及特点比较。

原理与方法

1.CCD设计

中心复合设计，多因素五水平的试验设计，有完全中心复合设计和小规模中心复合设计［2］，由2k析因设计或部分因子设计（规范化后通常用±l表示）加上2k个（k为因子数）坐标轴点（±α，0，0，…，0），（0，±α，0，…，0），……，（0，0，0，…，±α），和相应的nc个中心点（0，0，…0）组成。小规模CCD设计采用的是非对称的最小试验次数优化法，因子数与完全CCD设计不同；α的适当选择可以满足旋转性和实现试验的序贯性，改善预测精度，上述两种情况的α也是不同的，例如k＝3时完全CCD设计α＝1.682或1.732，小规模CCD设计α＝1.41；而中心点个数依因子数不同而不同，一般nc取4个以上。此设计的析因部分（图1中立方体的顶点），用于估计一阶项和交互作用项；轴向点（图1的星点）用于估计二阶响应曲面模型的纯平方项；中心点（图1立方体的中心）用于提供对一致精度和纯误差项的估计［3］。

2.模型的建立

基于CCD设计本身的特点，拟合二次响应面回归模型是合理的，通常采用的二阶模型表达式为：

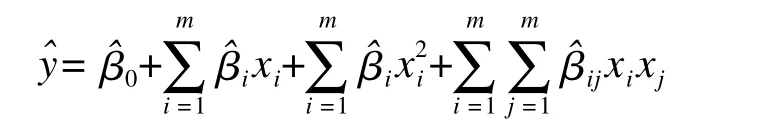
i＜j，m为因素个数。

图1 CCD设计（k＝3）

3.四种优化方法

（1）直接法

根据实验设计获得的试验数据和响应指标值限制条件，在设计的试验范围内直接寻找相对符合条件的最优解，即根据试验数据及分析结果，计算各因素不同水平下响应指标的平均值或合计，在因素间无交互作用时，选择各因素不同水平下响应指标的平均值或合计最大或最小时的因素水平为最优条件；在某些因素之间的交互作用有统计学意义时，首先要计算存在交互作用的因素各水平在试验中的各种组合条件下响应指标的平均值或合计，无交互作用因素最优条件选择同前，综合两类因素的结果，就可确定含有交互现象时各因素的最优条件［4］。

（2）最速上升（下降）法

沿着响应值有最大增量的方向逐步移动，直到响应不再增加（减少）为止，通常分析方法包括典型分析和岭脊分析：进行典型分析后，如果特征值有正有负，则进行岭脊分析，其原理是以原始设计中心点为球心、r为半径的超球面与响应面的交点形成的轨迹范围内找出最佳响应值，即最佳工艺条件［5］，此过程可通过SAS9.1 PROC RSREG完成。

（3）等高线法

通过绘制等高线图和响应曲面，结合优化条件，在系列图中找寻最优解，此过程在本文是通过Design-Expert V8.0.6.1完成。

（4）遗传算法

模仿自然界生物进化机制的随机全局搜索的优化方法，通过设置MATLAB单目标遗传算法程序的参数后搜索最优解。本文参数设置为初始种群＝30、单点交叉概率＝0.75、最大进化代数＝100时，随机进行20次搜索。

实例分析

1.数据资料

木糖降解需要木聚糖酶，经研究发现木聚糖酶在经链霉菌属P12-137发酵获得时其活性受木糖底物、硝酸钾含量、麦麸含量的影响，故试验的影响因素为麦麸、硝酸钾、木糖含量，而其响应指标为木聚糖酶含量。本项研究的试验设计是小规模CCD设计，其因素编码水平表和试验结果分别见表1、表2。

表1 因素编码水平

表2 CCD设计试验过程及结果

2.模型的建立及评价

利用Design-Expert V8.0.6.1软件，采用逐步筛选法（α入＝0.10，α出＝0.15）建立二阶响应模型为经方差分析得：所建的二次模型是有统计学意义的（F＝4.95，P＝0.0210），且拟合不足部分无统计学差别（F＝2.87，P＝0.1656），说明模型拟合是良好的。

3.试验条件的优化

最速上升法、等高线图法及遗传算法的寻优均是建立在上述所建模型基础上进行的，这是方法本身所决定的。

（1）直接法

X1与X2、X2与X3之间的交互作用项具有统计学意义，根据现有的设计水平组合，X1与X2分别在-1和1水平时，木聚糖酶含量较高为27.77 UA/m l，而X2与X3都为1水平时木聚糖酶含量较高，恰好为第七次试验方案，故直接法寻优结果：麦麸量为1%，硝酸钾为1%，木糖含量为0.5%时获得最大的木聚糖酶含量，为27.77 UA/m l。

（2）最速上升法

典型分析的特征值有正有负，所以需要进行岭脊分析，结果见表3，得出的木聚糖酶提取的最优条件为：麦麸量为1.88%，硝酸钾为0.16%，木糖含量为0.20%时获得最大的木聚糖酶含量23.93 UA/m l。

（3）等高线图

搜索的24次结果中1号相对最优，结果见图2，最优条件为麦麸、硝酸钾、木糖含量分别为0.80%、1.16%、0.80%时获得相对最大木聚糖酶含量47.07 UA/m l；另外由系列响应曲面图（图2右侧）可知X1与X2存在交互作用，且KNO3对响应影响较大。

图2 X3＝0.80，X1、X2变动时Y的等高线图与响应曲面图

表3 岭脊分析表

（4）遗传算法

由MATLAB2009a的单目标遗传算法程序搜索20次（仅列出8次，见表4），较理想的结果为麦麸、硝酸钾、木糖含量分别为0.83%、1.13%、0.72%时获得相对最大木聚糖酶含量51.04 UA/m l。

表4 遗传算法部分搜索结果

4.四种优化结果的比较

对于本试验数据寻优结果可知，遗传算法寻优的木聚糖酶含量比直接法、最速上升法、等高线法分别增加23.27 UA/m l、27.11 UA/m l、3.97UA/m l，提高了83.8%、113.3%、8.43%；在传统优化方法寻优结果中，等高线法、直接法比最速上升法增加了23.14 UA/ m l、3.84 UA/m l，提高了96.7%、16.0%。

讨 论

从优化方法的特点而言，直接法是在一定实验设计范围内通过求平均值寻找优化结果，可较快找出相对的最优解，不能保证局部或全局最优，但基于试验设计的优化，可为预试验或试验提供较理想的结果；等高线法亦基于试验结果基础上，通过软件绘制等高线时，仅两个因素可以在试验范围内变化，其他的因素保持在某个水平，而导致找出最优解过程相对于前者复杂和主观性强，但结果比较直观，可得出局部相对最优解和哪个因素影响大或是小，但不能保证在更大的空间范围内为最优，而且在试验为多因素多水平（因素在三或三个以上，在绘图时，需固定两个因素以外的其他因素，有时绘不出等高线）、多个响应指标时比较复杂，不易给出最优解；最速上升（下降）法通过求各因素偏导数基础上典型分析确定稳定点，若稳定点远离二次响应面模型的探测区域时，还需进行岭脊分析，随着因素增多，求解过程难度变大或不易求出，而且存在多目标优化时不能直接使用，最优解也只能是局部最优；本试验中遗传算法的结果和最速上升法相当，是由于本试验采用星点设计，拟合效果较好，已经接近最优点所在区域，所以最速上升法的效果才比较好，并不是最速上升法所有情况下优化效果都好。

从优化方法的效果而言，在这四种优化方法中等高线法及遗传算法优化效果最好，最速上升法次之，直接法处于相对劣势。造成这四种方法优化效果差别的原因：（1）四种优化方法本身的优化特点是不同的，而遗传算法始终是在全局范围内寻找最优解；（2）试验所选择设计类型及因素水平数不同，拟合的方程也将不同，所以建立在模型基础上的优化效果也是不同的。本项研究所采用的中心复合设计，拟合二次响应曲面方程，基于设计和模型的优化所确定的最优区域没有偏离真实的最优区域很远，所以传统优化方法尤其是等高图法与遗传算法的效果相差不大。

在选择优化方法时，因素较少、条件简单时可以使用传统的优化方法，直接法适用于粗略寻找最优解，如若要求较严格，可选用等高线法或是最速上升（下降）法；因素较多、条件复杂时应采用遗传算法。

1.刘艳杰，项荣武.星点设计效应面法在药学试验设计中的应用.中国现代应用药学杂志，2007，24（6）：455-457.

2.Draper NR，Lin DKJ.Small Response-Surface Designs.Technometrics，1990，32（2）：187-194.

3.胡雅琴，何桢.响应曲面二阶设计方法比较研究.天津大学，2005.

4.仇丽霞，刘桂芬.多因素试验优化算法及医学应用.山西医科大学，2003.

5.王黎明，夏文水.水法提取茶多糖工艺条件优化.食品科学，2005，26（5）：171-174.

（责任编辑：郭海强）

Com parison of Four M ethods on Optim izing Conditions by Using the Central Com posite Design

Feng Ruimei，Wang Ting，Dai Shuai，et al（ShanxiMedicalUniversity（030001），Taiyuan）

ObjectiveThe characteristics of the optimalmethods can be learned after carrying outa single objective optim ization bymeans of them.MethodsThe optimal parameter status of the production of xylanasesw ill be optim ized using the directmethod，the contoursmethod，the steepest rising or falling method and genetic algorithm.Based on the optimal results，we can come to some conclusions.ResultsThe production of xylanases after optim izing through the above four methods are 27.77UA/m l，23.93UA/m l，47.07UA/m l and 51.04UA/m l，respectively.ConclusionThe directmethod can find solutions in a short time，which may not be best in a local or a global area.In an optim izing example of a single objective designed by central composite design，the optimal effect of contoursmethod was closer to genetic algorithm；thatwhich factor wasmore influential can be observed in the contoursmethod，which can notavoid the defaults of the local optim ization and subjectivity.The steepest rising method was prone to giving the disadvantage solution while ignoring other advantage results.

Central composite design；Traditional optimalmethods；Genetic algorithm；Optimal parameter status

*：国家自然科学基金项目（30872183）

1.山西医科大学公共卫生学院卫生统计学教研室（030001）

2.Glasgow Caledonian University

△通信作者：仇丽霞，E-mail：qlx-1126＠163.com