基于“自适应遗传算法”的磁轴承系统辨识

赵 林，魏 彤

（北京航空航天大学 仪器科学与光电工程学院，北京 100191）

磁悬浮轴承是一种阻尼和刚度主动可控、非接触的支撑方式，与机械轴承相比，具有无摩擦、高精度、长寿命的优点[1]，近年来广泛应用于车床主轴等工业领域设备及飞轮、控制力矩陀螺等航天领域设备[2]。

准确掌握系统模型是提高磁轴承系统的控制精度、稳定性及可靠性的基础。将自校正控制[3]等先进的控制方法及干扰观测器、前馈补偿等扰动抑制方法应用于磁轴承系统可以提高磁轴承系统的控制精度及稳定性，对磁轴承系统进行故障诊断[4]和容错控制则可大幅度提升系统可靠性，这些方法均需要磁轴承系统的即时系统模型参数，而对磁轴承进行系统辨识是获取系统模型参数的重要手段。

系统辨识的一般方法是基于某一种优化准则，对系统参数进行最优估计。系统辨识的优化准则包括最小方差准则、广义误差准则和输出误差准则。以最小方差为准则的方法，如极大似然法[5]、卡尔曼滤波[6]，以及以广义误差为准则的方法，如最小二乘法 LS（least square）[7-8]、梯度校正法等，这些方法使用线性优化方法，计算量小，在系统噪声为白噪声的情况下有较高精度。对于系统噪声为有色噪声的情况，极大似然法和上述算法的一些衍生算法，如自适应卡尔曼滤波算法[9]、偏差补偿最小二乘法[10-11]、广义最小二乘法[12]等方法，在已知噪声方差阵或者统计特性的情况下精度较高。但是，在磁轴承系统辨识中，噪声特性会受温度、湿度或输入信号的频谱宽度等各种因素的影响而发生变化，因此使用上述方法辨识精度会受到较大影响。基于输出误差准则的方法，由于输出误差与系统参数为非线性关系，往往将待辨识参数作为优化参数，将输出误差的一个标量函数作为优化的目标函数，用最优化算法对其进行优化，这种方法在不知道噪声统计特性的情况下仍然有较高精度。由于在磁轴承系统辨识中，难以求出目标函数对优化参数的导数，传统的优化方法无法使用，而近年来发展迅速的现代智能算法不依赖于问题本身的数学性质，可以解决这类最优化问题。现代智能算法通常分为单值优化算法和群优化算法，其中单值优化算法中常用的方法有爬山算法、禁忌搜索和模拟退火等方法，这类算法较容易陷入局部最优解；群优化算法有遗传算法GA（genetic algorithm）[13]、粒子群算法 PSO（particle swarm optimization）、蚁群算法 ACO（ant colony op timization）、人工蜂群算法 ABC（artificial bee colony）等，这类算法与单值优化算法相比往往更易得到全局最优解。这些算法中，“自适应遗传算法”具有最坚实的理论基础，应用最为广泛，并且可以有效降低标准“遗传算法”中“早熟”现象出现的概率。

本文对磁轴承原理样机进行系统辨识实验，分别使用目前应用广泛的卡尔曼滤波和“自适应遗传算法”对其进行系统辨识，后者辨识的准确性大幅度提高，验证了方法的有效性。

1 单通道磁轴承系统模型

磁轴承系统单通道结构原理如图1所示。

图1 磁轴承系统单通道结构图Fig.1 Single-channel structure of the magnetic bearing system

本文中所使用的磁轴承系统采用不完全微分的PID控制器，其传递函数为

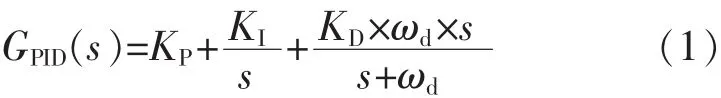
磁轴承系统中，功率放大器具有饱和非线性，当输入信号的频率和幅值较小时，可以对其进行近似线性化，等效为一阶低通环节，传递函数为

磁轴承转子采用差分电流控制，转子所受电磁力为

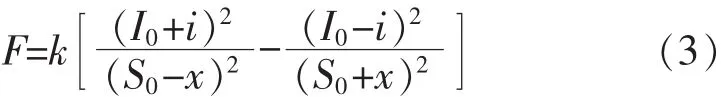
式中：k为与磁导率、线圈匝数及铁芯横截面积等有关的比例常数；I0为偏置电流；S0为名义气隙。转子位移较小时，可作近似线性化处理，将 F（i，x）在 F（0，0）处泰勒展开，仅保留一阶项，得到轴承力的近似线性化表达式：

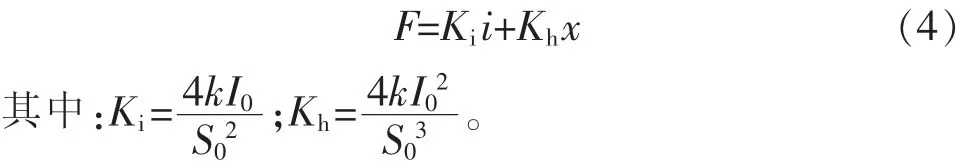
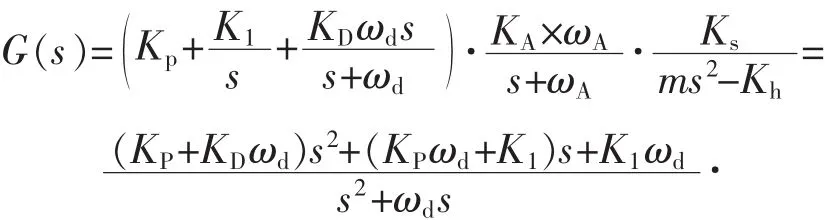
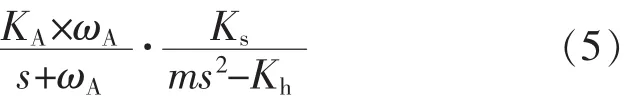
对应的磁轴承系统轴向通道的系统框图如图2所示。由于辨识使用离散数据，采用双线性方法对式

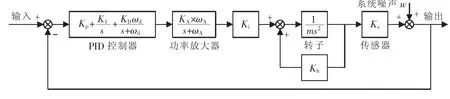
图2 磁轴承轴向通道系统框图Fig.2 Diagram of axialmagnetic bearing system

（5）离散化，离散传递函数仍为5阶，得到：

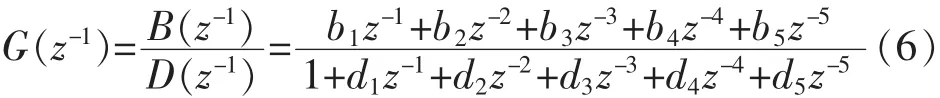
利用图2中输入和输出数据进行辨识，首先辨识出系统闭环系统参数：

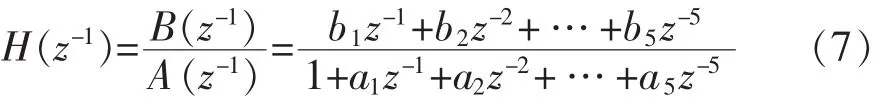
辨识出闭环系统参数 θ0＝［a1，a2， …，a5，b1，b2，…，b5］T后，根据闭环和开环传递函数的关系式 H（=进一步计算出开环系统参数 θ＝［d，d，）G12…，d5，b1，b2，…，，其中 di=ai-bi，i=1，2，…5，为自适应控制、故障诊断等提供系统开环模型。虽然实际磁轴承系统的功率放大器、转子环节具有一定非线性特性，当转子位移较小时，线性化后的模型基本可反映系统真实特性。

2 基于“自适应遗传算法”的磁轴承系统辨识方法

磁轴承系统各变量示意图如图3所示。以输出误差为准则的系统辨识方法则是求出模型参数使得输出误差 e的一个标量函数最小，这里设为。

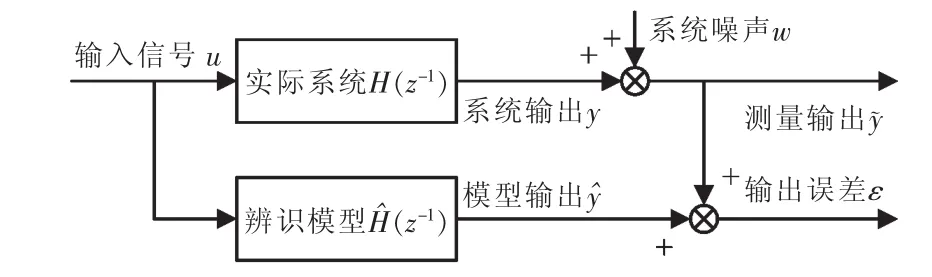
图3 输出误差示意图Fig.3 Schematic of output error

由图3可得：

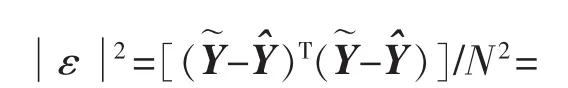
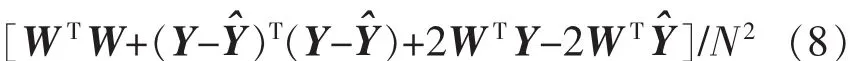
都是确定信号，而w是零均值随机信号，通常假设 w 和 y、ˆ相互独立，亦即

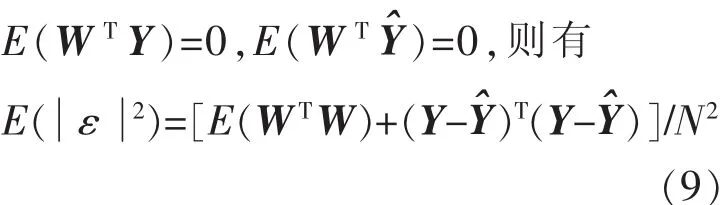
由于E（WTW）为仅与噪声方差有关的常数，而（Y（Y-≥0，所以在 E（）取最小值时必然有YY，进而有因此只要噪声 W 和 Y、独立统计，以输出误差为准则的辨识方法辨识精度便不受噪声有色特性影响。

各染色体的交叉概率和变异概率的计算公式为

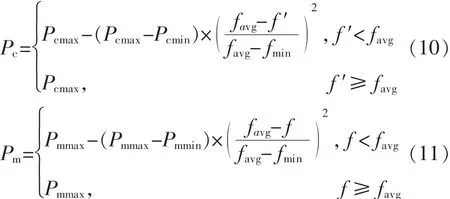
其中：Pcmax、Pcmin、Pmmax、Pmmin分别为当前种群最大、最小交叉概率和最大、最小变异概率；f′为参与交叉的两个染色体的较小适应度；f为变异染色体的适应度。Pcmin和Pmmin与上一代的种群相同，而Pcmax和Pmmax的计算公式为

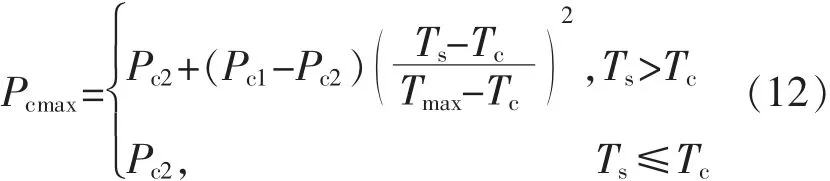
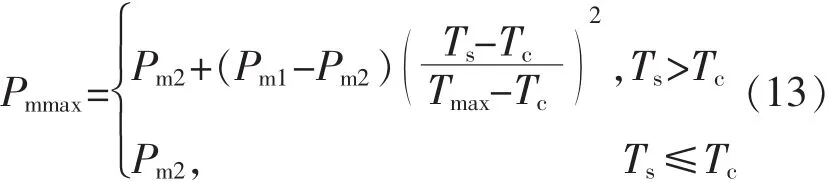
其中：Pc1、Pc2、Pm1、Pm2为进化过程中的最大、次大交叉概率和最大、次大变异概率；Tmax为设定的最大遗传代数；Ts为最优个体适应度连续不变的代数；Tc为控制参数。这样，当种群进入停滞状态时，适当加大了种群的交叉概率和变异概率，从而增加了种群的多样性，帮助种群尽快打破僵局，有效防止早熟。

3 实验

采用实验室自行研制的磁悬浮控制力矩陀螺系统进行实验，设备如图4所示，主要包括：磁悬浮控制力矩陀螺、电源、电路板以及数据采集系统等。输入信号为M序列电压信号，采样频率为1 kHz。

图4 实验用磁轴承系统Fig.4 Experimentalmagnetic bearing system

磁轴承在长期运行中随着温度、湿度等环境因素的变化以及其他影响因素的影响，其输出端噪声的频谱宽度难以确定，因此在实验中在输出端叠加不同频带宽度的噪声信号，来验证在不同频带宽度的噪声信号的影响下“自适应遗传算法”均有较高精度。其辨识结果如表1所示。

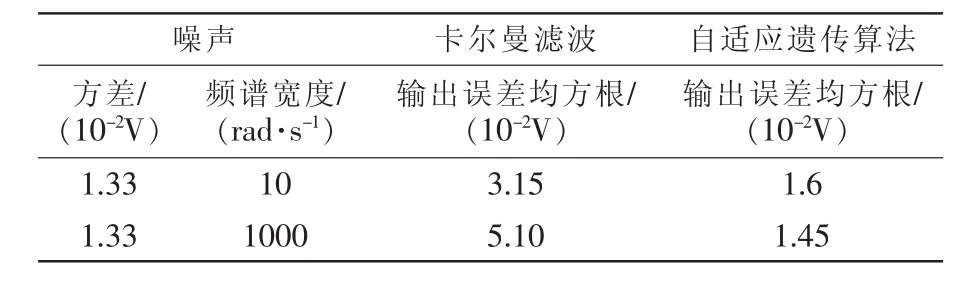
表 1 两种算法对实际系统辨识结果Tab.1 Identification results of two algorithms for the actual system

从表1可以看出，自适应遗传算法在噪声频谱宽度为10 rad/s和1000 rad/s时均有较高精度，而卡尔曼滤波算法由于频谱宽度的增加辨识精度下降。

图5为表1最后一组数据，即频谱宽度为1000 rad/s时，系统输出与卡尔曼滤波、自适应遗传算法辨识模型输出的比较结果。从图中可以看出，磁轴承系统输出信号的数据点均匀分布在自适应遗传算法辨识模型输出的两端，而卡尔曼滤波辨识模型输出与系统输出之间有较大误差，说明在这种噪声的影响下卡尔曼滤波辨识结果有一定误差，而自适应遗传算法仍然有较高精度，与仿真结果一致，进一步验证了方法在有色噪声条件下该方法的有效性。

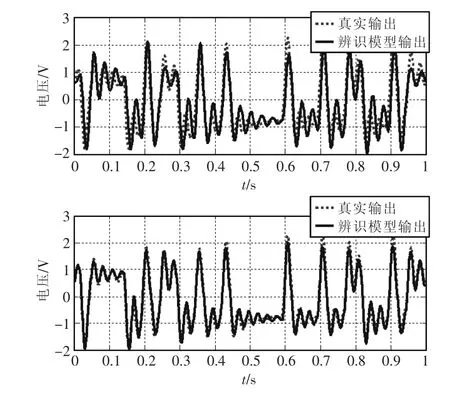
图5 真实系统输出与各辨识模型输出比较图Fig.5 Com parison chart between real system output w ith the identification model output

4 结语

现有的磁轴承系统辨识方法由于受有色噪声干扰，辨识精度较低，无法满足应用要求。本文利用自适应遗传算法对此轴承系统模型进行辨识，这种方法以输出误差均方根作为适应度，在进化过程中考虑了整体种群的进化程度，使交叉概率和变异概率在停滞阶段适当增加，从而避免种群“早熟”。实验结果表明，这种方法与具有较高辨识精度的“卡尔曼滤波”相比精度大幅度提高，充分验证了方法的有效性。

[1] R Amano，S Kamada，T Sugiura.Dynamics of a flexible rotor with circumferentially non-uniform magnetization supported by a superconducting magnetic bearing[J].IEEE Trans.Applied Superconductivity，2013，23（3）：2104-2107.

[2] B Han，S Zheng，X Hu.Dynamic factor models of a thrust magnetic bearing with permanent magnet bias and subsidiary air gap[J].IEEE Trans Magnetics，2013，49（3）：1221-1230.

[3] N S Gibson，G D Buckner.Real-time adaptive control of active magnetic bearings using linear parameter varying models[C]//in Proc.IEEE of 2002 Southeast Conf.，Columbia，SC，2002.

[4] R Gouws，G Schoo.A comparative study on fault detection and correction techniques on active magnetic bearing systems[C]//Proc.of 2007 Africon，Windhoek，2007.

[5] V B Tadic Analyticity，convergence，and convergence rate of recursive maximum-likelihood estimation in hidden markov models[J].IEEE Trans.Info.Theory，2010，56（12）：6406-6432.

[6] J Hu，X L Ding.Kalman-filter-based approach for multisensor，multitrack，and multitemporal InSAR[J].IEEE Trans Geoscience and Remote Sensing，2013，51（7）：4226-4239.

[7] C Gahler，R Herzog.Identification of magnetic bearing systems[C]//4th Int.Symp.on Magnetic Berings，ETH Zurich，1994.

[8] C G R Herzog.Multivariable identification of active magnetic bearing systems[C]//5th Int.Symp.on Magnetic Bearings，Kanazawa，1996.

[9]V Venkataraman，G L Fan，J P Havlicek.Adaptive Kalman filtering for histogram-Based appearance learning in infrared imagery[J].IEEE Trans Image Processing，2012，21（11）：4622-4635.

[10]K Ikeda1，Y Mogami1，T Shimomura1.Bias-compensated least squares method in closed loop enviornment estimation under coloured noise[C]//in Proc.2009 ICROS-SICE Int.Joint Conf.，Fukuoka，2009.

[11]A Bertrand，M Moonen，A H Sayed.Diffusion bias-compensated RLS estimation over adaptive networks[J].IEEE Trans.Sig.Processing，2011，59（11）：5212-5224.

[12]N Qiu，Q S Liu，Q Y Gao，et al.Combining genetic algorithm and generalized least dquares for geophysical potential field data optimized inversion[J].IEEE Geoscience and Remote Sensing Letters，2011，7（4）：660-664.

[13]Ip，WH DingweiWang.Aircraft ground service scheduling problems and their genetic algo rithm with hybrid assignment and sequence encod ing scheme[J].Systems Journal，IEEE，2013，7（4）：649-651.

[14]任海艳，陈飞翔.自适应遗传算法的改进及在曲线化简中的应用[J].计算机工程与应用，2012，48（11）：152-155. ■