基于Fluent的仿生机器鱼胸鳍摆动模型仿真分析

冯静安，晁贯良，王卫兵，牛建文，邱艳军

(石河子大学机械电气工程学院，新疆石河子 832003)

基于Fluent的仿生机器鱼胸鳍摆动模型仿真分析

冯静安，晁贯良，王卫兵，牛建文，邱艳军

(石河子大学机械电气工程学院，新疆石河子 832003)

为研究胸鳍攻角对仿生机器鱼升潜运动的影响，制定机器鱼升潜运动控制规则，分析了升力产生的机制和影响因素，建立了机器鱼胸鳍摆动数学模型，根据机器鱼胸鳍几何模型，应用Gambit建立了机器鱼胸鳍二维网格模型，应用Fluent仿真，分析了不同攻角下机器鱼升力阻力差，确定胸鳍在来流速度为0.5 m/s的水动力环境下做周期摆动时的最佳攻角为20°左右。

机器鱼;胸鳍;摆动模型;Fluent仿真

生物学研究发现，在所有的海洋物种中，鱼类的游动方式效率最高，相对于传统的螺旋桨驱动，鱼类的游动还具有高机动性、高隐蔽性的特点，因此，越来越多的中外学者展开了对仿生机器鱼的研究［1－6］。

机器鱼实现上浮、下潜运动，主要通过以下四种方式［7］:在鱼体中内置泵和水箱，通过调整自身重力与浮力差实现升潜运动;改变尾鳍矢量推进方向，如将尾鳍旋转90°，则原来的转弯运动变为升潜运动;改变机器鱼重心位置，使鱼体与水平面成一定角度，在推进的同时实现升潜运动;通过胸鳍上下摆动产生的升力实现升潜运动。

文中所述机器鱼采用BCF模式推进方式，通过胸鳍在一定攻角下做周期摆动产生的升力实现升潜运动。通过建立仿生机器鱼胸鳍摆动数学模型，应用Gambit建立机器鱼二维几何网格模型，通过Fluent仿真，分析机器鱼在胸鳍做周期性摆动时，不同攻角下的升力阻力差，分析胸鳍最佳攻角，为制定仿生机器鱼升潜运动控制规则奠定基础。

1 翼型薄板升力机制

机器鱼在静水中或稳定匀速流场中游动，其速度比较低，雷诺数属中等雷诺数范围 (103＜Re＜106)。为了对胸鳍进行受力分析，对流体进行以下简化处理:流体稳定均匀、密度均匀且不可压缩、非黏性、无穷远处流体不受干扰，因此机器鱼运动受力问题可以简化为无黏性流体问题。

依照无黏性流体理论，定常流体中运动的封闭物体，可以分解出一个垂直于其相对运动方向的力，即升力。

如图1所示，b为弦长，c为翼的弦线，α为翼弦与来流v∞的夹角，称为攻角。翼型表面上各点都作用有摩擦力和压强，水翼上摩擦力F2和总压力F1，产生合力F。将F按平行于v∞方向和垂直于v∞方向分解为Fx和Fy，Fx为阻力，Fy为升力。

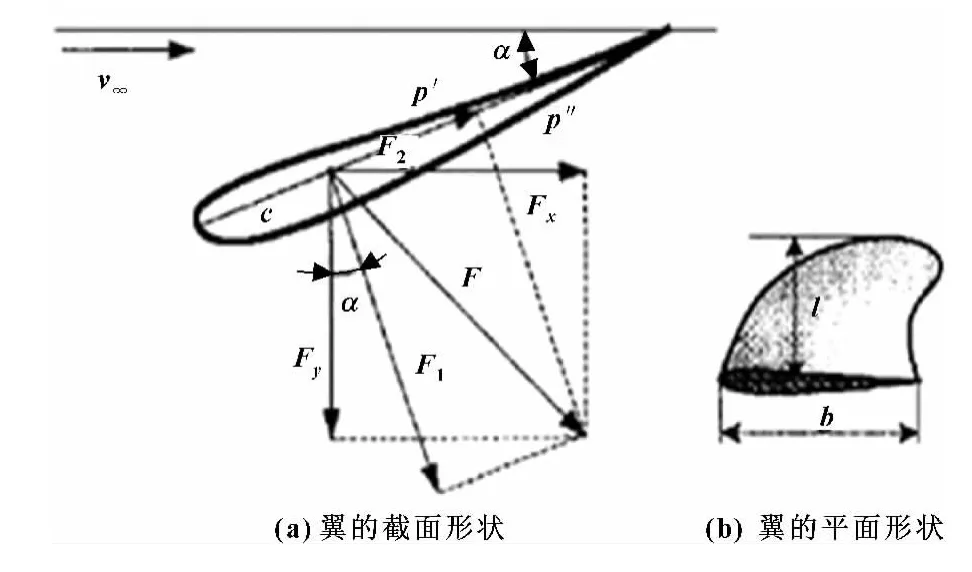
图1 水翼参数与受力分析

2 升力影响因素分析

根据量纲一化流体动力系数定义:

式中:l为翼的展长;

b为弦长;

v∞为来流速度;

ρ为流体的密度;

Cy、Cx为流体动力系数。

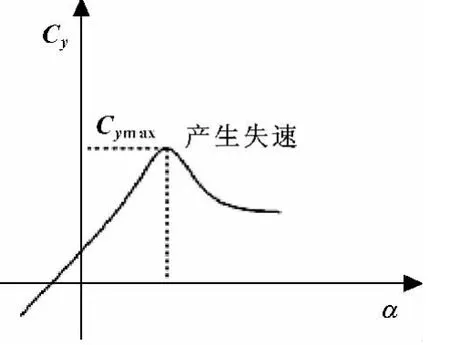
图2 升力系数与攻角之间的关系

当直线低速流动的均匀流体以v∞、小α流过水翼时，翼型阻力主要是附体流动产生的摩擦阻力，因此Cx值较小且随α变化不大，随着攻角α的增大，上下翼面压差增大，升力近似线性增加;当攻角增大到某临界值后，下翼面的附体流动被破坏，出现粘性压差阻力增量，Cx值急速增大，升力迅速下降，此临界攻角称为失速角。升力系数与攻角间的关系可由图2所示。

同时，假定流体密度ρ不变，由式 (1)可知，升力Fy与升力系数Cy、来流速度v∞、翼的展长l、弦长b成正比。

3 胸鳍建模

3.1 胸鳍摆动数学模型

假定机器鱼在游动过程中，躯体的前2/3没有摆动，即没有摇首动作，刚性胸鳍仅做绕轴摆动，其运动模型如图3所示。

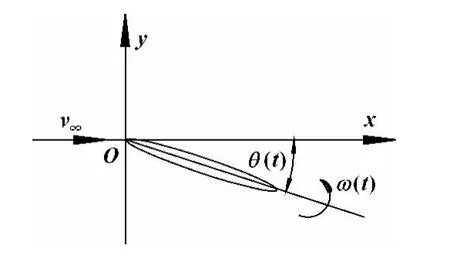
图3 胸鳍运动模型

胸鳍的运动规律可以表示为:

式中:θ0为胸鳍的最大摆角，rad;

f为摆动频率，Hz。

摆动速度可以表示为

胸鳍末端位置变化规律:

式中:A为胸鳍最大摆幅，A=Lsinθ0;

L为胸鳍展长。

整个胸鳍的纵向位置坐标方程为:

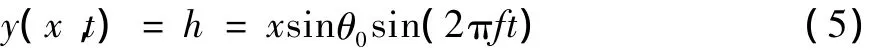
式中:x，y为机翼坐标;t为运动时间。

3.2 胸鳍几何模型

胸鳍几何结构模型如图4所示，展长为77 mm，最大厚度为12 mm，宽度为50 mm，机翼平面位于xOy平面内，转动轴位于距离前端7 mm处绕z轴周期摆动。

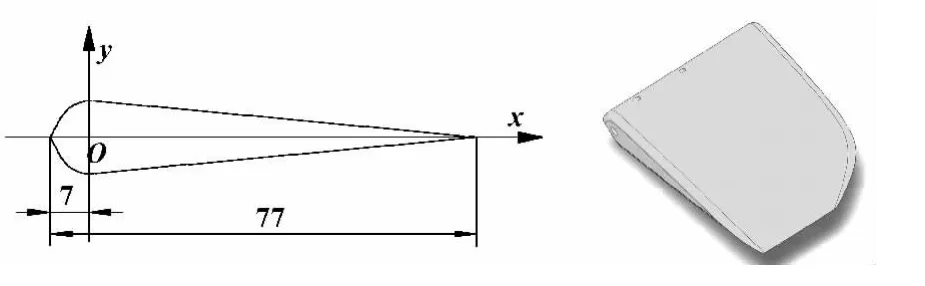
图4 胸鳍几何结构模型

3.3 二维网格模型

应用Gambit建立胸鳍二维几何模型，并生成网格。计算区域采用上下6倍展长，尾部10倍展长的长方形区域，以减小边界对运动的影响，网格划分结果如图5所示。

图5 胸鳍二维网格划分模型

4 Fluent仿真

4.1 仿真参数设置

(1)边界条件设定

如图3所示，流场左边界定义为速度入口 (Velocity Inlet)，右边界定义为出口边界 (Outflow)，上下边界为对称边界 (Symmetry)，胸鳍为壁面边界条件(Wall)。

(2)动域的确定

将胸鳍定义为动域，根据胸鳍摆动数学模型，通过UDF编程加载到fluent中。

(3)动网格参数设置 (如表1所示)

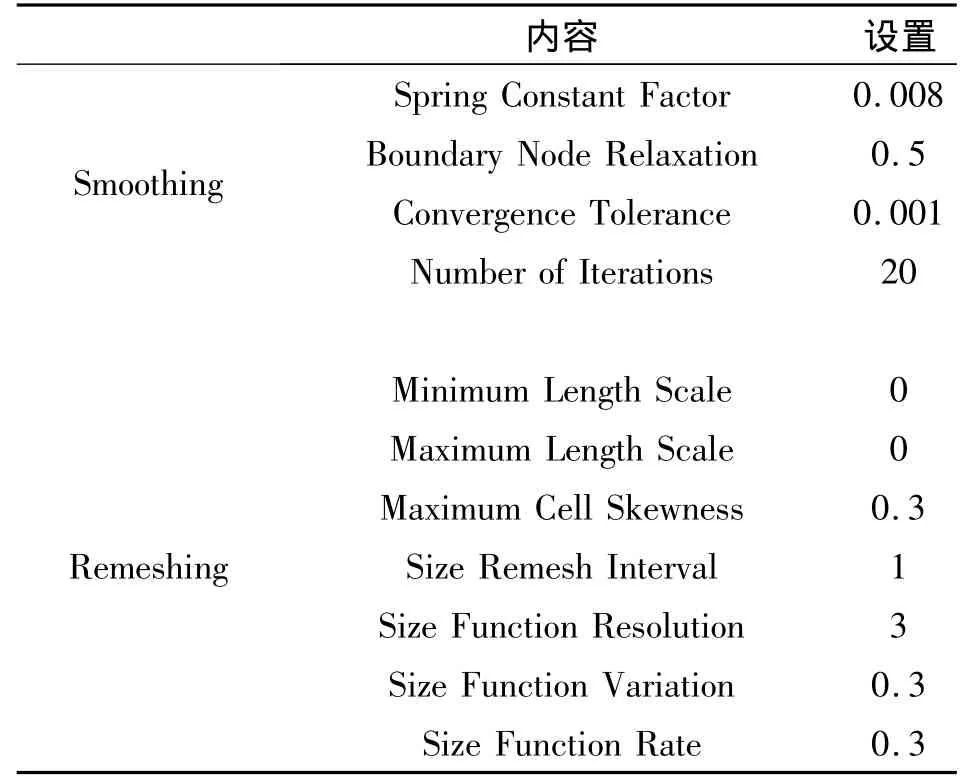
表1 动网格参数设置

(4)Fluent求解参数设置 (如表2所示)

表2 Fluent求解参数设置

4.2 仿真结果分析

不同攻角下的升力阻力仿真结果如图6—10(图中的横坐标Flow Time，单位为s;纵坐标中Cd为阻力系数，Cl为升力系数)所示。

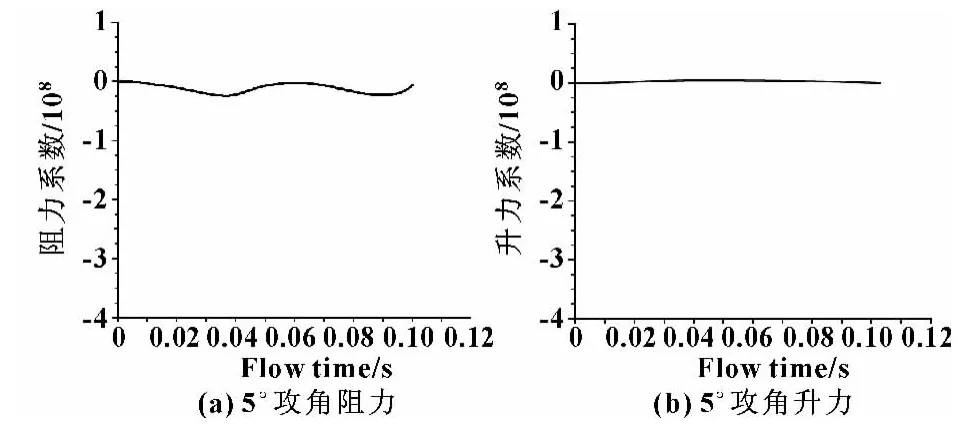
图6 5°攻角升力阻力曲线

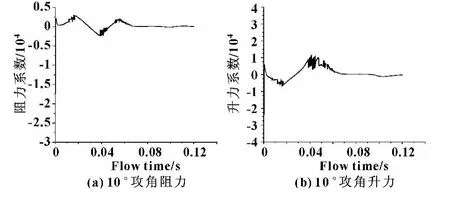
图7 10°攻角升力阻力曲线

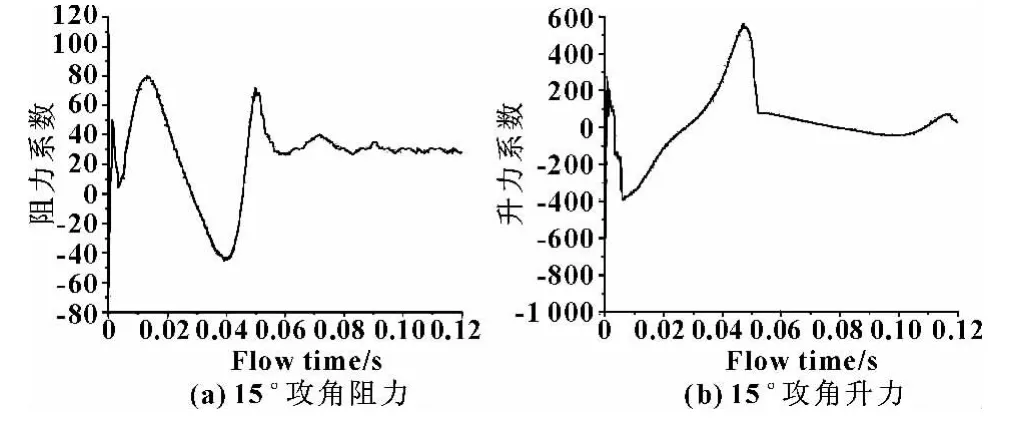
图8 15°攻角升力阻力曲线

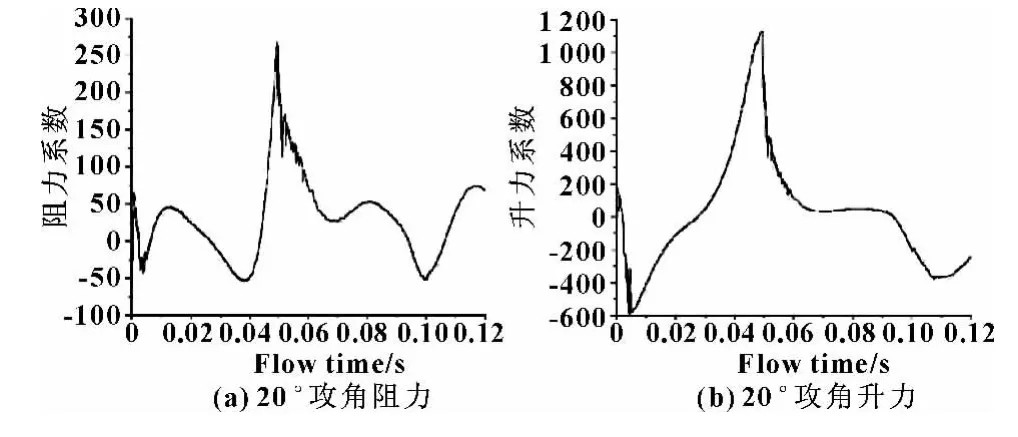
图9 20°攻角升力阻力曲线

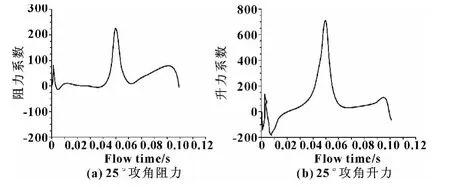
图10 25°攻角升力阻力曲线

由图6可知:升力与阻力基本重合，其差值基本为0，说明胸鳍在5°攻角摆动时，升潜效果不明显。分析图7—10发现:各攻角在半个周期附近升力与阻力差呈现最大值，这是由于胸鳍在一定攻角下做绕轴摆动时胸鳍与水平面的夹角一直在变化，当到达半个周期时夹角呈现最小值;出现最大差值的位置在小范围内波动，可能是由于在摆动时受到涡流的影响。通过5组图对比可以发现，20°攻角以前升力随攻角呈递增关系，而阻力增加不明显，之后攻角再变大时，阻力没有太大变化，而升力则有明显下降趋势，这是由于攻角过大时对流场的扰动相应增大。由此可以确定，攻角在20°左右为机器鱼上浮下潜的最优角度。

5 结论

胸鳍摆动式仿生机器鱼通过胸鳍攻角的变化引起胸鳍升力与阻力差，实现机器鱼的升潜运动;在一定范围内，攻角增大，升力增加，升力阻力差增大，但攻角超出一定值后，升力迅速下降，升力阻力差减小;通过对来流速度为0.5 m/s的环境下对做周期性摆动的胸鳍进行不同攻角下的水动力学模拟分析，确定机器鱼升潜运动最佳攻角为20°左右。

［1］徐义刚，万德成.刚性胸鳍运动参数的优化［J］.力学季刊，2012，33(2):210－220.

［2］魏鹏.低航速减摇鳍的升力特性分析及控制方法研究［D］.哈尔滨:哈尔滨工程大学，2011.

［3］彭之春，庞永杰.机器鱼的运动仿真方法［J］.系统仿真学报，2004，16(12):2643－2646.

［4］蔡月日，毕树生.胸鳍摆动推进模式仿生鱼研究进展［J］.机械工程学报，2011，47(19):30－37.

［5］徐一村，宗光华，毕树生，等.胸鳍推进机器鱼俯仰稳定性分析［J］.机器人ROBOT，2012，34(3):376－379

［6］WANG Weibing，YU Junzhi，DING Rui，et al.Bio－inspired Design and Realization of a Novel Multimode Amphibious Robot［C］.IEEE International Conference on Automation and Logistics，Shenyang，China，August5－7，2009:140－145.

［7］朱兴华.一种仿生机器鱼的运动分析及其控制系统研究［D］.哈尔滨:哈尔滨工程大学，2005.

Simulation and Analysis of Bionic Robo-Fish Swing Model Based on Fluent

FENG Jingan，CHAO Guanliang，WANG Weibing，NIU Jianwen，QIU Yanjun
(College of Mechanical and Electrical Engineering，Shihezi University，Shihezi Xinjiang 832003，China)

To research the influence of attack angle on the bionic robo-fish in dive motion，the robo-fish dive motion control rules was made，the lift with generation mechanism and influence factors was analyzed，and the swing model of pectoral fin was established.According to the geometry model of pectoral fin，the pectoral fin of robo-fish two-dimensional grid model was established by applying the software of Gambit.And applying Fluent software simulation，the robo-fish lift and resistance difference under different attack angle was analyzed，the pectoral fin optimal angle of attack is about 20°at flow velocity of 0.5 m/s in hydrodynamic environment with doing periodic swing was determined.

Robo-fish;Pectoral fin;Swing model;Fluent simulation

TP391.9

A

1001－3881(2014)9－124－3

10.3969/j.issn.1001－3881.2014.09.034

2013－04－11

国家863计划项目 (2007AA04Z202);国家自然科学基金项目 (60865004)

冯静安 (1977—)，男，硕士，在读博士，讲师，主要从事机械 CAD/CAM研究。E－mail:fja_mac@ shzu.edu.cn。通信作者:王卫兵，E－mail:wwbshz@163.com。