综合孔径辐射计亮温反演算法研究

黄传禄 晁 坤 毛云志

（中国电波传播研究所，山东 青岛266107）

引 言

综合孔径辐射计引入射电天文中“孔径综合”的概念，通过小孔径阵列等效合成大孔径，利用干涉测量、相关处理等技术，有效提高了辐射计的空间分辨率，成为当前辐射计研究和发展的热点［1-5］.综合孔径辐射计亮温反演成像的基础是利用干涉测量得到的可视度函数反演成像得到观察区域的辐射亮温分布［1-2］.在远场条件及系统理想的情况下，可视度函数与修正亮温分布呈傅里叶变换关系，而且所有相同长度和取向的基线具有相同的干涉测量结果，从而可以使用稀疏天线的布局，避免了大口径天线的加工困难及机械扫描问题，并可以在一定程度上缓解由于积分时间引起的空间分辨率和温度分辨率的矛盾［1-2］.

综合孔径亮温反演从本质上属于空域傅里叶变换［3-4］，其阵列参数决定了系统的空间分辨率、观察范围、反演结果精度等重要指标.为了简化阵列结构，获得尽可能多的空间频率点，综合孔径辐射计稀疏阵列的组合形式是设计中的关键问题，对此已有许多深入的研究［1，6-7］.反演中G矩阵求逆运算直接关系反演结果的误差，因此在设定阵列参数时需要十分谨慎［1，4］.

消条纹函数，也称为梳状（Fringe Wash）滤波函数，描述了各阵元之间传输延时造成的空间解相关效应，对系统性能具有重要影响［2，7-8］.在窄带信号、阵列孔径不太大且各通道特性完全一致的理想情况下，消条纹函数值接近于常数1，从而空间解相关效应可以不考虑.然而在实际应用中，为了提高辐射计的灵敏度，综合孔径辐射计尽量采用大的通道带宽，当阵列孔径造成的信号延时与系统带宽的倒数可比拟时，便不再满足阵列窄带信号的假设［7］.此时，综合孔径反演算法中空间解相关效应不可忽略.此外，实际系统中的各个通道的特性并非完全一致，也会造成空间解相关效应.因此，消条纹函数在综合孔径辐射计亮温反演中占据重要位置，传统的反演算法（如快速傅里叶变换（Fast Fourier Transform，FFT）算法，（Backus-Gilbert，BG）算法等）中忽略消条纹函数的影响，必然带来反演误差［8-9］.

本文从空域傅里叶变换角度分析了综合孔径阵列各参数的设计约束，采用一维均匀等距线阵为例，探讨了阵元间距和阵元数以及阵列波束宽度等对综合孔径系统性能的影响.根据干涉测量基本原理，通过消条纹函数分析了系统带宽以及通道特性造成的空间去相关效应对反演误差的影响.基于BG算法，分析了G矩阵相关性对亮温反演误差的影响.利用消条纹函数建立了考虑带宽效应和通道不一致性时的误差校正模型.

1 理论分析

1.1 综合孔径辐射计阵列参数分析

综合孔径辐射计通过相关干涉测量获得可视度函数，可视度函数与目标亮温分布呈傅里叶变换关系［1］.综合孔径辐射计实际上是在空间频率域上进行采样，采样值即为可视度函数值.

为简化分析，采用一维均匀线阵进行分析，设阵元间隔为d，阵元数为N.图1为综合孔径辐射计信号处理中傅里叶变换关系示意图.如图1所示，频域采样间隔为u1＝d／λ，频域采样孔径为us＝Nu1.在空域中间隔xs＝1／us，空域周期即口径x1＝1／u1.

图1 综合孔径空域傅里叶变换示意图

空间域x＝sinθ，可见，空间域由空间角度决定，因此空域也称为角域.空域即阵列观测区域，一般取阵列上半空间，即对应角度范围为［-90°，90°］，则x范围为［-1，1］.

设阵列波束范围为［-θL，θL］，按照傅里叶变换性质，为无失真的恢复采样信号，应满足

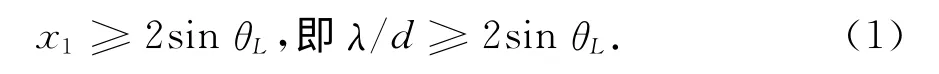
为保证全方向无模糊，即在［-90°，90°］范围内无失真采样，应具有d≤λ／2，即频域采样间隔u1≤0.5.

1.2 综合孔径辐射计亮温反演算法

设接收通道中心频率为fc，系统带宽为B，一般B≪fc，可以当作窄带随机过程来处理［1］.设两接收阵元天线的激励电压为VT（θ，t）和VT（θ，t-τ）.τ＝Δr／c为时间延迟.两天线单元的接收电压分别为

式中，Θ为天线方向图积分区域.经过功分、乘法运算及低通滤波得到如下复相关输出

由于Va（t）和Vb（t）为遍历信号，可认为时间平均等价与集平均.＜VT（θ，t），VT（θ′，t）＞是信号的功率，它与天线方向图加权的亮度温度T（θ）成正比.式（3）可表示为

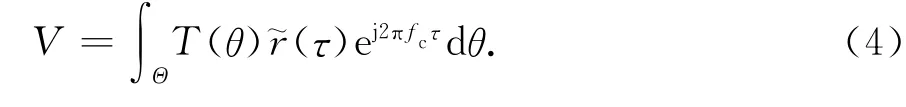
式中：Gi表示i通道最大增益；Bi表示i通道的等效噪声带宽；对于一维阵列，τ＝dsinθ／c.

式（4）即建立了亮温与可视度函数的对应关系.由式（4）可以建立亮温反演模型，将积分离散化为

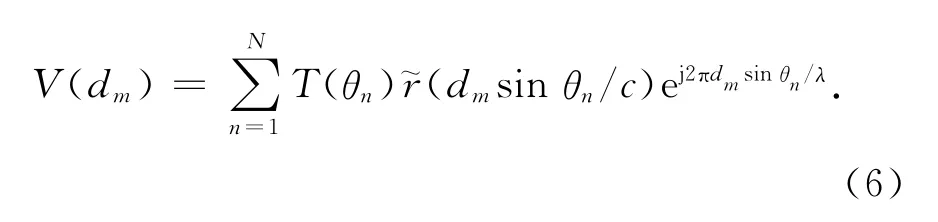
式中：θn为空间第n个区域角度；dm为第m对基线长度.

1.3 BG算法中G矩阵相关性分析

在实际应用中，为便于降低反演误差，亮温反演中一般采用BG算法.根据式（6），并忽略消条纹函数影响，可得如下矩阵方程

式中：V为M×1的可视度函数向量，M＝2 N＋1，N为等效一维均匀线阵的阵元数；T为Np×1为目标亮温分布向量；G为M×Np的傅里叶变换矩阵.因此，反演过程即由M个可视度函数反演Np个亮温，一般Np＞M，因此过程是欠定的，并且往往是病态的.采用最小二乘法求解矩阵方程（7），得

式中：G＋为G的广义逆矩阵［2］.BG算法的核心是构造G矩阵，并且求其广义逆G＋.G矩阵的相关性，严重影响求逆运算的稳定性和准确性.当矩阵的条件数很大时，矩阵是病态的，求逆结果很不稳定，误差增大.

G矩阵中第i列的导向矢量为

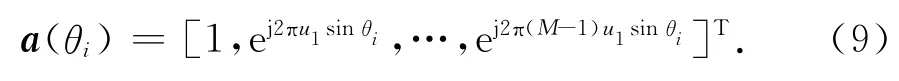
式中，θi为目标辐射信号的入射角度.

定义G矩阵任两矢量的内积为

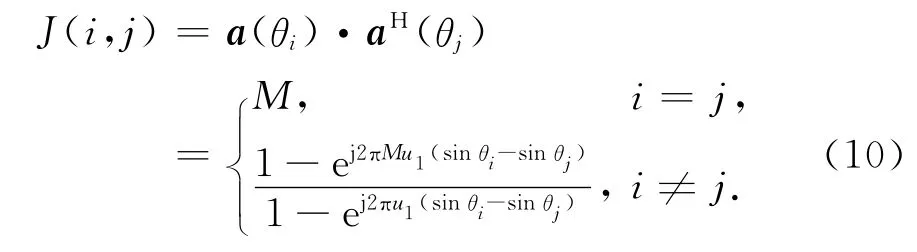
内积J（i，j）可以描述两矢量的相关性，J（i，j）越大，则相关性越大.当分母项为零，即2πu1（sinθi-sinθj）＝2πK，K为非零整数时，J（i，j）取极大值.G矩阵的相关性由其任意两列矢量相关性的综合效果决定，这里取各矢量相关性的均方值来定义G矩阵的相关性为

设目标区域按正弦值均匀划分，共分为Np个区域，间隔为Δx＝2sinθL／（Np-1）.如果存在

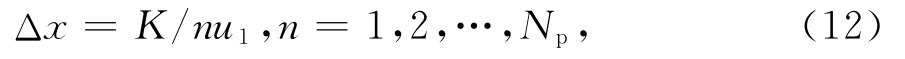
则表明其中两矢量相关性陷入极值，G矩阵条件数非常大，求逆运算误差将极大.因此，在设计空间分辨率时，应选取合适的区域间隔，使G矩阵相关性最小，以减少求逆误差，从而降低亮温反演误差.

1.4 空间解相关效应分析

由sinc函数特性，在｜πBτ｜接近0时，函数值接近1，式（6）中可以忽略（τ）的效应.按照阵列信号理论，当πB≪｜1／τ｜时，信号定义为阵列窄带信号，此时空间解相关效应可以忽略［1］.

理想矩形带通滤波器在实际中是物理不可实现的，为了模拟现实系统中通道的带通特性，采用如下的二阶系统来描述通道特性：

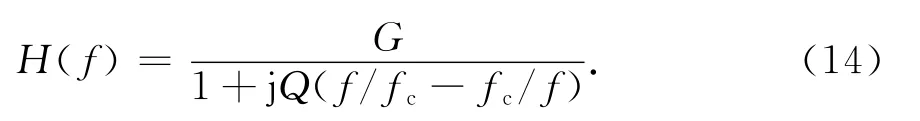
式中：G为通道最大增益；Q＝fc／Δf为品质因数；Δf为系统3dB带宽.将其带入式（5）中即可得到（τ）表达式.

按照式（5），除了带宽的影响外，通道不一致性也会造成空间解相关效应［10］.因此，利用消条纹函数，可以建立考虑带宽误差和通道不一致性误差的校正模型.

式（6）描述的方程，转化为如下矩阵方程：

式中：G是维数为M×N的傅里叶变换矩阵，同式（7）定义一致，G（m，n）＝ej2πdmsinθn／λ；Gr是维数为M×N的消条纹函数修正矩阵，也叫去相关矩阵，Gr（m，n）＝（dmusinθn／c）.对Gr·G求解广义逆，得到亮温的最小二乘解.

2 仿真分析

以Ka波段综合孔径辐射计为例进行仿真分析，假设等效阵元数N＝90；波束范围-35°～35°.

由式（1）计算得到d／λ≤0.87，否则会产生频谱混叠造成反演失真.图2及图3为阵元间隔波数u1分别为0.5和2时，信号频谱图和亮温反演结果.由图2可以看出，当阵元间隔为0.5时，频谱采样没有混叠，包含了目标的大部分频率分量.因此经过反演，能较准确地恢复原始信号.而如图3所示，当间隔波数为2时，频谱产生混叠，在高频部分出现较大失真分量.

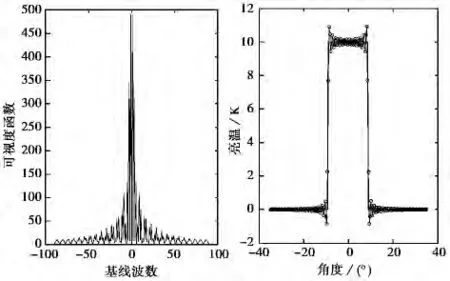
图2 u1＝0.5时可视度函数值和反演亮温

由图2可以看出，反演结果在目标亮温变化部分出现振荡.这实际上是频域采样时对高频截断造成的吉布斯振荡效应.由图2中的信号频谱图可以看出，综合孔径阵列采样时最高只采到2 Nd／λ的频率分量，其余的高频分量被舍弃导致高频分量截断，因此在反演中出现高频振荡［2］.在实际系统中，阵列孔径不可能无限增加，因此高频振荡效应无法完全消除，但可以采用加窗的方式降低其影响［3］.

图3 u1＝2时可视度函数值和反演亮温

在u1＝0.87时，按照式（11）计算的G矩阵相关性最小处对应的区域划分点数分别为181.由上述分析可得，u1＝0.87的阵列在频域内采样数为181，因此经过傅里叶变换在空域仅能准确得到181个目标亮温值，更多的反演目标点由这181个点插值得到.这点也可以从矩阵理论上分析得到，G矩阵为行满秩，其行秩为M，即可视度函数的数目［1］.因此G矩阵求逆后，只有M行是线性无关的，其余的行向量都由该M行向量线性组合得到.

图4给出了在u1＝0.87时，选取区域划分数目分别为140、181及543时，反演的亮温结果.由图4（b）看出，目标划分点数为140时，反演结果误差非常大.这是因为此时G矩阵相关性极大，从而导致求逆误差很大.图4（c）为选取最佳反演点数即181时反演结果，其反演非常准确，误差很小.图4（d）为选取3倍反演点数时反演结果，可以看出，其误差相比181点数时较大，但与原目标相比仍比较准确.而此时反演结果更加平滑.因此在实际应用中可以选取3倍最佳点数，反演结果更加平滑，同时反演误差和计算时间也可以接受.

下面计算分析空间解相关效应对亮温反演的影响.采用一维稀疏阵列，单元数为16，最小间隔为0.5λ.通道特性如式（14）描述，通道3dB带宽为200MHz，等效噪声带宽为300MHz，假设各通道特性完全一致.

图5为对应的消条纹函数曲线.如图所示，该消条纹函数为一单边减幅余弦信号，在τ＝0时，函数值为1.设阵元最大基线长度（即阵列口径）为2m，天线方向图区域为［-40°，40°］，则计算可得最大延时约为3.3ns.由图5可以看出该时延值下，消条纹函数值约为0.3，其代表的空间解相关效应不可忽略.从另一角度计算，此时Bτ≈1，不满足阵列窄带信号定义，因此其空间解相关效应必须进行补偿.另外，计算发现，当πBτ＜0.5时，消条纹函数大于0.95，即误差在5%之内，空间解相关效应可以忽略.

图4 不同划分数目时亮温反演结果

图6给出了点目标反演仿真结果.在角度0°和6.5°设置了两个点目标，其亮温为1K.如图6所示，在采用无修正的BG算法时，反演结果误差很大，在利用式（15）考虑消条纹函数修正模型后，反演结果与目标亮温非常接近.图7为区域［-40°，40°］范围内连续分布目标反演结果.可以看出修正算法显著地改善了由空间解相关效应造成的误差.

图5 消条纹函数

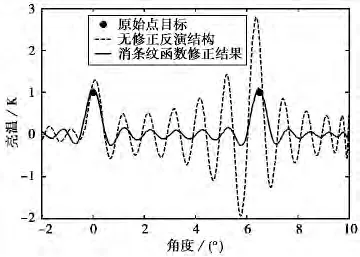
图6 点目标反演结果

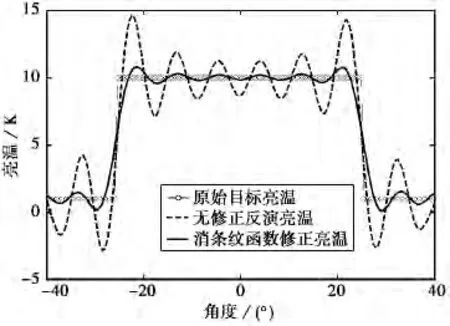
图7 连续目标反演结果

从图6和图7还可以看出，在阵列法线位置附近时，消条纹函数造成的误差很小，而随着角度增大，误差变大.两阵元的时延为τ＝dsinθ／c，因此角度增加时，时延也会增加，从而使空间解相关效应增大，误差增大，本文模型对解相关效应进行补偿后，消去了该误差.

由上面分析，利用消条纹函数，可以补偿两阵元时延造成的空间解相关效应，同时对通道增益、相位不一致性等进行修正.但对阵元位置误差，阵元互耦等误差不能完全进行补偿修正.由式（15）可以看出，阵列位置误差会同时影响消条纹函数矩阵Gr和傅里叶变换矩阵G，需要对两矩阵同时进行修正，对阵元位置误差和阵元互耦误差进行校正也是当前综合孔径辐射计的研究热点［9-10］.

3 结 论

本文基于空域傅里叶变换规律分析了综合孔径亮温反演算法，分析了G矩阵相关性对反演结果的误差影响.利用干涉测量中消条纹函数建立了空间解相关效应修正矩阵.理论及仿真计算发现，设计空间分辨率时，应使G矩阵相关性较小，以降低矩阵求逆误差.空间解相关效应随观测角度和阵元间距的增加而变大，并与系统带宽和阵元间信号时延有关，当πBτ较小时，可假设为阵列窄带信号，从而忽略其效应.在工程应用中，一般选取πBτ＜0.5即可满足要求.

本文的研究对综合孔径辐射计实际参数的设计具有指导意义，对综合孔径辐射计中带宽效应和通道不一致效应的研究都具有应用价值，对进一步研究亮温反演误差校正也具有参考意义.

［1］吴 季，刘 浩，阎敬业，等.干涉式被动微波成像技术［J］.遥感技术与应用，2009，24（1）：1-12.WU Ji，LIU Hao，YAN Jingye，et al.Interferometric imaging technology for passive microwave radiometry［J］.Remote Sensing Technology and Application，2009，24（1）：1-12.（in Chinese）

［2］LEVINE D M，SWIFT C T，HAKEN M.Development of the synthetic aperture microwave radiometer，ESTAR［J］.IEEE Transactions on Geosciences and Remote Sensing，2001，39（1）：199-202.

［3］孙逢林，张升伟.基于综合孔径辐射计稀疏阵列非均匀采样图像的快速重建［J］.电子与信息学报，2013，35（4）：927-932.SUN Fenglin，ZHAN Shengwei.Fast image reconstruction for non-uniform sampling of thinned array of synthesis aperture radiometer［J］.Journal of Electronics ＆Information Technology，2013，35（4）：927-932.（in Chinese）

［4］晁 坤，陈后财，赵振维.综合孔径辐射计反演成像算法研究［J］.电波科学学报，2011，26（5）：881-887.CHAO Kun，CHEN Houcao，ZHAO Zhenwei.Image reconstruction and inversion algorithm of synthetic aperture radiometer［J］.Chinese Journal of Radio Science，2011，26（5）：881-887.（in Chinese）

［5］LEVINE D M，JACKSON T J，HAKEN M.Initial images of the synthetic aperture radiometer 2D-STAR［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45（11）：1355-1368.

［6］王玲玲，方大纲.运用遗传算法综合稀疏阵列［J］.电子学报，2003，31（12）：2135-2138.WANG Lingling，FANG Dagang.Genetic algorithm for the synthesis of thinned array［J］.Acta Electronica Sinica，2003，31（12）：2135-2138.（in Chinese）

［7］TANNER A B，SWIFT C T.Calibration of a synthetic aperture radiometer［J］.IEEE Transactions on Geosciences and Remote Sensing，1993，31（1）：257-267.

［8］赵 锋，苗俊刚，胡岸勇.二维综合孔径微波辐射计误差分析［J］.微波学报，2008，24：197-201.ZHAO Feng，MIAO Jungang，HU Anyong.System errors analysis of aperture synthesis microwave radiometers［J］.Journal of Microwaves，2008，24：197-201.（in Chinese）.

［9］郭 强，谢利子，冯小虎，等.综合孔径微波辐射计互耦模型与校正方法［J］.电波科学学报，2012，27（1）：122-127.GUO Qiang，XIE Lizi，FENG Xiaohu，et al.Mutual coupling model and calibration method for synthetic aperture microwave radiometer［J］.Chinese Journal of Radio Science，2012，27（1）：122-127.（in Chinese）

［10］王 鼎，吴 瑛.基于旋转不变子空间均匀圆阵互耦自校正算法［J］.电波科学学报，2011，26（2）：253-261.WANG Ding，WU Ying.Mutual coupling self-calibration algorithm for uniform circular array based on ESPRIT technique［J］.Chinese Journal of Radio Science，2011，26（2）：253-261.（in Chinese）