中国区域科技成果转化效率研究—基于DEA和SFA的比较分析

吴佩佩，刘家树，齐 昕

（安徽工业大学经济学院，安徽马鞍山243032）

近年来，随着国家创新体系的构建，科技成果产出数量不断攀升的同时，越来越多的学者开始关注科技成果转化问题。2011年国内专利申请授权数为96.1万件，全国共发表科技论文53万篇，这些知识产出在多大程度上带动生产率和经济效益的提高，的确是各创新主体面临的一个问题。由于我国科技资源投入不足的刚性束缚以及资源配置机制的瓶颈制约，我国科技成果转化情况不甚理想。因此，对我国区域科技成果转化绩效进行分地区核算，将有助于把握科技成果转化现状，对促进科技与经济发展互融并进具有重要意义。

国外对科技成果转化效率的研究有：Wahab等[1]从知识和组织学习视角，运用相关系数和多重线性回归方法对4大技术转移特性进行分析，发现关系特征对隐性知识和显性知识转移的效率影响最大。Anderson等[2]运用DEA方法对大学技术转移效率进行测算，并探讨学校的公立和私立性质是否会对技术转移的效率产生影响，结果表明学校的所有权性质对技术转移效率没有影响。Jiang[3]对技术创新联盟的知识转移效率进行了研究。国内对科技成果转化效率也进行了一些研究，如徐晨等[4]运用DEA方法对我国30多个地区（不含港、澳、台）的科技成果转化绩效进行分析，得出我国科技成果转化水平整体较低。刘家树等[5]基于我国大中型工业企业省际面板数据，运用DEA模型，对科技成果转化效率进行测度，发现我国大中型工业企业科技成果转化效率不高。杨宏进等[6]以2007年我国高校科技成果产出均处于效率前沿的省份为研究对象，在国内首次运用三阶段DEA模型对高校科技成果转化进行效率分析。

上述文献中非参数的DEA方法得到了大量运用，其优点在于不需要估计生产函数，而且可以考虑多产出；其缺点是不能衡量随机误差对个体绩效水平的影响，也不能对生产过程进行描述。而参数的SFA方法则可以将随机扰动项分解为随机误差项和技术无效项，并利用计量方法进行效率估计。但是SFA方法用于科技成果转化效率测算的研究国内少见报道，鉴于此，同时避免单一研究方法的局限性，本文将DEA方法和SFA同时用于我国科技成果转化效率的测算，以期对我国科技成果转化情况进行更合理的描述。

1 研究方法与数据处理

1.1 DEA方法

DEA（Data Envelopment Analysis,数据包络分析方法）是由运筹学家Charnes等1978年提出，以输出/输入作为相对绩效而发展起来的评价决策单元相对有效性的非参数方法，本文使用基于产出的CCR模型[7]。

1.2 SFA方法

SFA是一种基于生产前沿面理论的参数方法，根据Battese等提出的面板数据模型,随机前沿生产函数模型的一般形式可以表示为

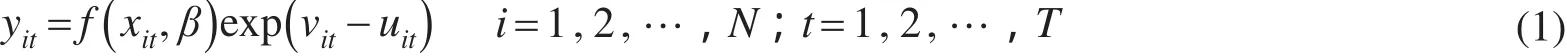
其中：yit表示产出；xit表示投入向量；β为待估计的参数。误差项为复合结构的分布以半正态分布和截断的正态分布为常见[8]。

1.3 变量选择与数据来源

科技成果转化的投入指标从资本投入和劳动投入2方面选取，文中分别为各地区研究与发展（R&D）经费内部支出额和各地区R&D人员全时当量。产出指标选取新产品销售收入。因为科技成果转化是技术成果商品化的过程，最终转化为新产品销售收入。事实上该指标也是有缺陷的，由于新产品销售收入的数据在《中国科技统计年鉴》是分行业的，因此本文新产品销售收入的数据选取大中型工业企业的新产品销售收入。

研究2003—2009年的中国科技成果转化情况。由于成果转化的滞后性，文中滞后期选择为1年。研究对象为中国大陆的省级行政区域，西藏由于部分数据缺失未计入文中。研究的时间跨度为7年，考虑到通货膨胀或通货紧缩对投入和产出的影响，文中计算了各省区2004—2010年各年份的GDP平减指数，将数据统一为2003年价格。所使用的原始数据来源于2004—2011年的《中国科技统计年鉴》和《中国统计年鉴》。

2 实证与结果

2.1 DEA测算结果

利用DEAP2.1软件测算各地区2003—2009年间科技成果转化效率，结果如表1。

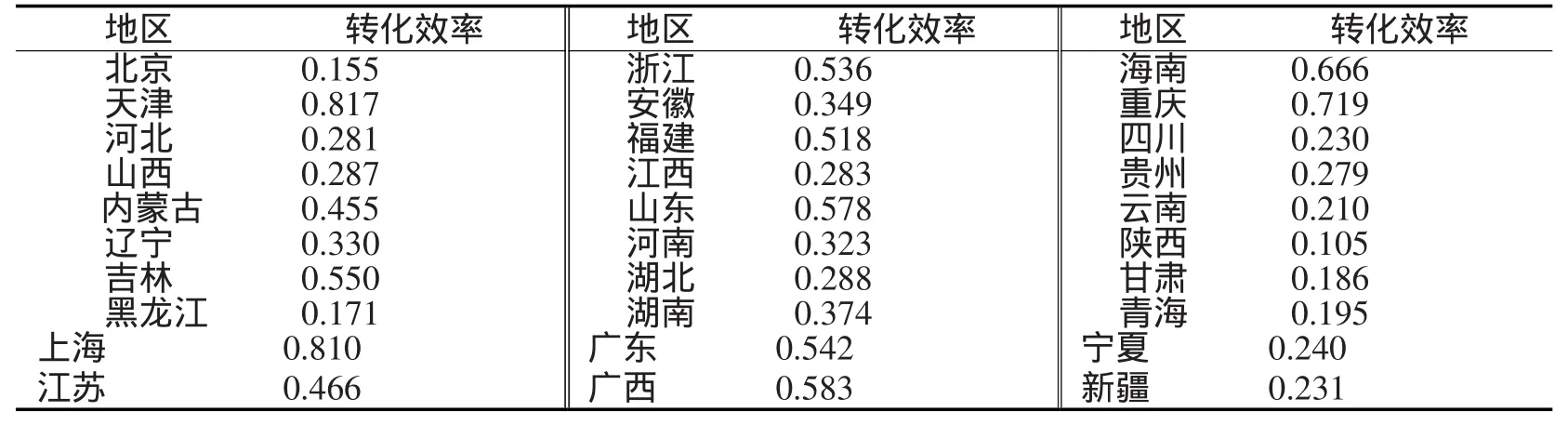
表1 DEA方法下各地区科技成果转化效率Tab.1 Transformation efficiency of regional science and technology achievements under DEAmethod

表1中数据为2003—2009年中国各地区科技成果转化的技术效率均值，全国均值水平为0.392。技术效率水平排在前5位的是天津、上海、重庆、海南、广西，其中天津、上海、海南位于东部地区，重庆、广西位于西部地区。而经济发展水平比较发达的江苏、浙江、广东、山东等省市科技成果转化的效率仅位于全国中等水平。北京、黑龙江、陕西、甘肃、青海等地的科技成果转化效率不足0.2，最低。

2.2 SFA测算结果

利用SFA方法进行效率测算，生产函数模型的选择是关键。目前，随机前沿分析选用的函数形式主要是柯布道格拉斯生产函数（C-D生产函数）和超越对数生产函数。C-D生产函数的优点是模型形式简单、参数少，便于估计，缺点是假定要素的替代弹性不变。超越对数生产函数放宽了要素间替代弹性不变的假定，同时允许非中性的技术进步的存在，但缺点是模型比较复杂，在多种要素投入的情况下，容易引发多重共线性问题[9]。本文根据Battese等的模型分别构建C-D生产函数和超越对数生产函数模型，然后根据参数估计结果选择最合适的模型进行效率估计。C-D生产函数模型为

式中：yit为第i个地区t期的新产品销售收入；Kit为第i个地区t期的R&D经费支出额；Lit为第i个地区t期的R&D人员投入量；β为待估计的参数。超越对数生产函数模型为

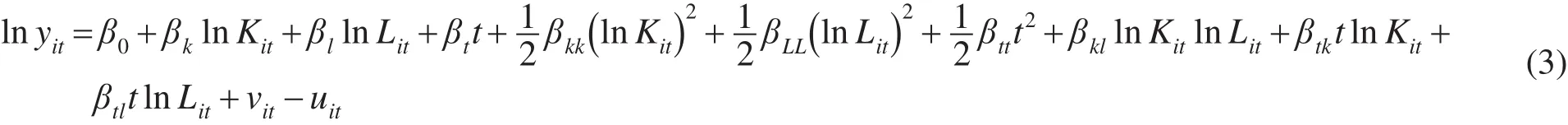
若式(3)中的二次项系数和交叉项系数为0，则超越对数函数变成C-D生产函数。

模型的假设检验有：

1)技术非效率检验 假设不存在技术非效率，那么随机前沿生产函数模型就变成普通的面板数据模型，只包含随机误差项的影响，用普通的OLS方法进行分析即可，不需使用SFA方法。为此，需要检验技术非效率不存在的零假设H0∶γ=0。

2)生产函数形式检验 检验C-D生产函数和超越对数生产函数，哪个更加适合。为此，需要检验零假设H0：βkk=βll=βtt=βkl=βtk=βtl=0。

3)技术进步检验 用t和t2代表技术进步变量，不存在技术进步的零假设H0∶βt=βtt=βtk=βtl=0。

4)技术非中性检验 技术中性指技术进步与投入要素无关，在超越对数模型中，用时间与投入要素的交叉项来衡量技术非中性，零假设H0∶βtk=βtl=0。

5)技术效率时变性检验 技术效率是否随时间变化，需要检验零假设H0∶η=0，当η=0时，表明技术效率不随时间变化。

6)技术非效率半正态分布检验 可利用截断正态分布模型的估计量来进行零假设检验，零假设H0∶μ=0，表示技术非效率项服从半正态分布。

7)半正态分布和时变性检验 零假设H0∶η=μ=0，表示技术效率不随时间变化，且非效率项服从半正态分布。上述7个检验都可以采用“广义似然比（LR）”统计量来检验

其中：lnL(H0),lnL(H1)分别是零假设H0和备择假设H1下模型的对数似然函数值，检验统计量服从χ2分布，自由度为约束变量的数目。如果计算出来的LR统计量大于临界值，则拒绝零假设，反之则接受零假设。

利用Frontier4.1软件对各种假设条件下的模型进行回归，结果见表2。

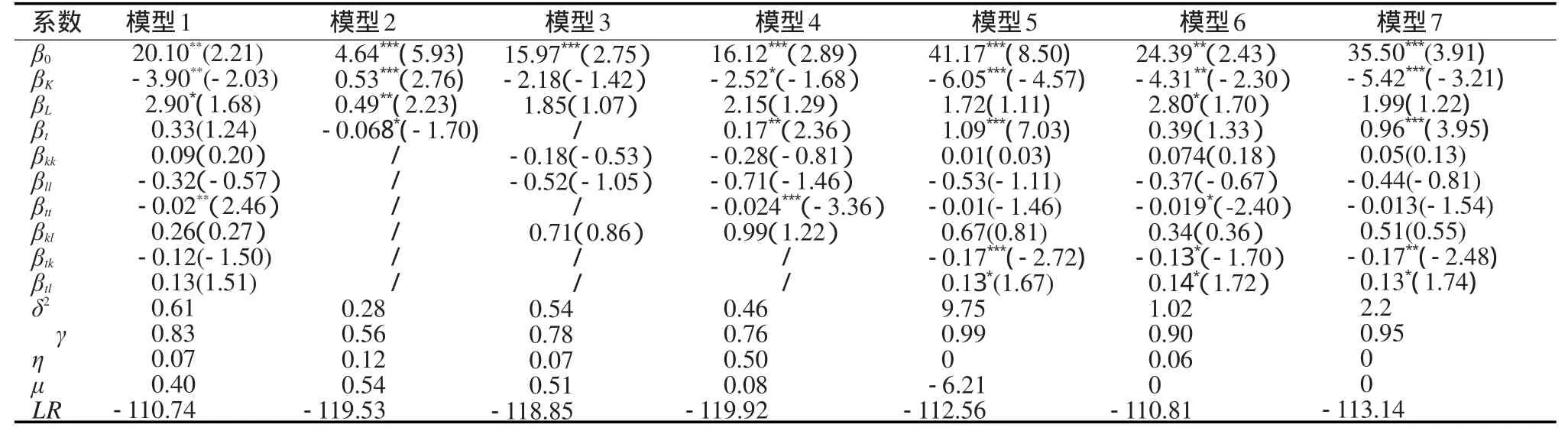
表2 不同假设条件下模型的回归结果Tab.2 Regression results under different assumptions

表3进一步给出了各种假设条件的检验结果，首先是SFA方法必要性的检验，假设1和假设2的零假设被拒绝，说明采用SFA方法是合理的；假设3的零假设被拒绝，说明超越对数函数模型比C-D函数模型更适合；假设4被拒绝，说明模型中需要考虑技术进步因素；假设5被接受，说明模型中的技术是中性的；假设6被接受，说明技术效率不随时间变化；假设7被接受，说明技术非效率项服从半正态分布；假设8被接受，说明技术效率不随时间变化同时技术非效率项服从半正态分布。

表3 假设检验结果Tab.3 Hypothesis testing results

根据检验结果，重新设定模型形式如式(5)。

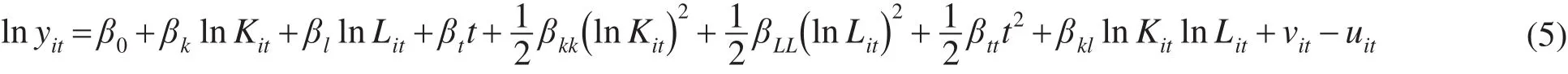
测算各地区2003—2009年间科技成果转化效率，结果见表4，全国均值为0.503。

由表4可知，天津以0.926的效率水平位于全国科技成果转化第一位，紧随其后的是重庆、上海、山东、广东、浙江等省市。排名前六的地区中除了重庆是西部城市外，其余的都是东部省市。河北、山西、内蒙古、辽宁、安徽、河南、湖北、湖南科技成果转化效率比较接近，这些地区大部分位于中部，经济发展水平也较接近。西部地区的云南、陕西、甘肃、青海、宁夏、新疆等地科技成果转化效率相对滞后，与东部某些地区差距较大。

2.3 DEA和SFA结果的比较

对比表1和表4的结果可发现，不管是各地区的效率值还是全国均值，SFA方法测算的值均大于DEA测算值，这是由于SFA方法将随机扰动项分解为随机误差项和技术无效项，而在DEA方法中所有的误差项都被归入技术无效项中，这样便会过高估计决策单元的技术无效率程度。为进一步分析科技成果转化效率的地区差异，有必要对两种方法计算结果进行聚类分析，即将科技成果转化效率最接近的地区划为一类。为便于和全国三大区域的划分进行比较，本文仍将科技成果转化效率分为三类，分别为科技成果转化高效区、科技成果转化中效区和科技成果转化低效区。借助SAS9.0统计软件进行聚类分析，具体结果见表5。

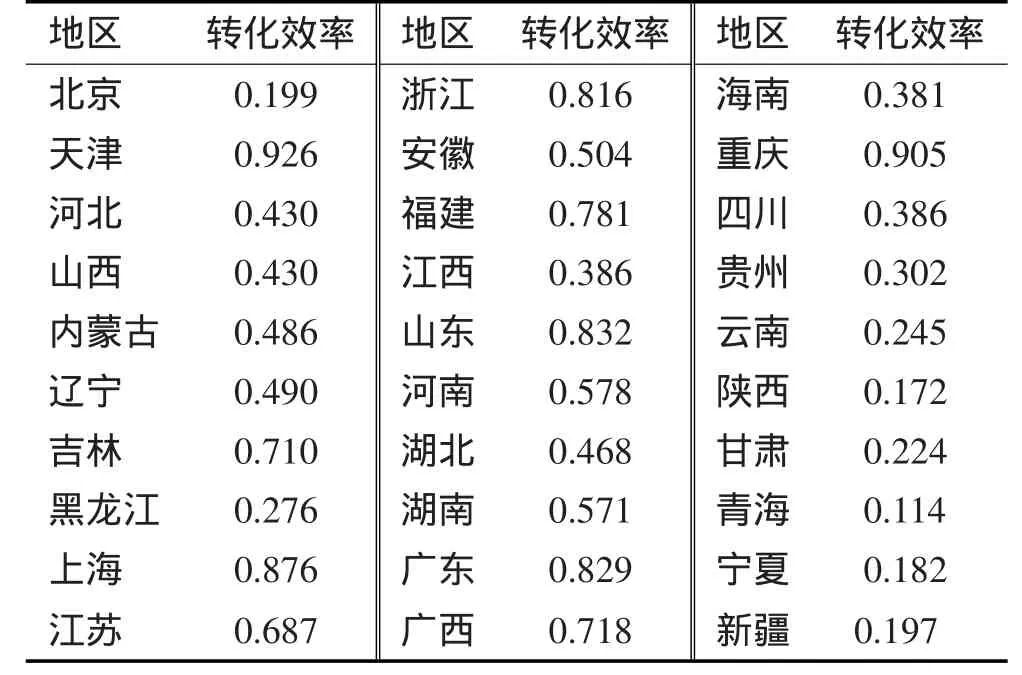
表4 SFA方法下各地区科技成果转化效率Tab.4 Transformation efficiency of regional science and technology achievements under SFAmethod

表5 地区科技成果转化效率聚类结果Tab.5 Clustering results of efficiency of regional scientific and technological achievements

由表5中可看出，用DEA方法测算的结果和SFA方法测算的结果进行聚类，聚类结果差别较大。DEA结果聚类中，科技成果转化的高效区只有天津、上海、海南、重庆，而在SFA结果聚类中，除了天津、上海、重庆之外，山东、广东、吉林、广西、浙江、江苏、福建也划分至科技成果转化高效区。科技成果转化中效区，DEA结果聚类显示有山东、广西、浙江、广东、内蒙古、江苏、吉林、福建，这其中经济发展水平较高的山东、广东、浙江、江苏等地，科技成果转化水平只位于全国中等水平，而在SFA结果的聚类中，中效区有河北、山西、江西、四川、内蒙古、辽宁、海南、河南、湖南、安徽、湖北。科技成果转化低效区，根据DEA测算的结果聚类有山西、湖北、四川、新疆、河北、江西、贵州、辽宁、河南、甘肃、青海、宁夏、北京、黑龙江、云南、安徽、湖南、陕西，共18个省市；在SFA结果的聚类中有北京、新疆、陕西、宁夏、云南、甘肃、黑龙江、贵州、青海，共9个省市。对比DEA、SFA聚类结果和地区分类，发现基于SFA方法的聚类结果和地区分类拟合性更好，一般来说，一个地区经济越发达、基础设施越完善、市场化水平越高，科技成果转化水平就会越高。东部地区11省市除了北京、河北、辽宁、海南外，其他7省市都位于SFA结果聚类的科技成果转化高效区中；中部地区8省都位于SFA结果聚类的科技成果转化中效区中；西部地区11省市中广西被划分至科技成果转化高效区，内蒙古、重庆、四川划分至科技成果转化中效区，其余7省被划入科技成果转化低效区。从SFA方法自身的优势以及两种方法的聚类结果，可以看出SFA方法测算的科技成果转化效率比DEA方法测算的更为合理。

3 结 论

本文利用2003—2009我国省级面板数据，运用DEA方法和SFA方法对各地区科技成果转化效率进行测算，结果表明：

(1)现阶段我国科技成果转化整体效率仍处于较低水平，DEA效率水平仅为0.392，SFA结果显示的我国科技成果转化整体效率水平为0.503，比DEA结果要大，因为DEA方法中所有的误差项都被归入技术无效项中，这样便会夸大决策单元的技术无效率程度。

(2)两种方法的聚类结果显示，参数的SFA方法比DEA方法更好描述各地区的科技成果转化现况。

(3)我国科技成果转化工作地区差异明显，东部地区科技成果转化效率最高、中部居中、西部地区科技成果转化效率最低。

综上，促进科技与经济融合，加速科技成果转化仍是是各地区都要重视的一个问题；消除科技成果转化区域差异，中西部地区应完善相关的政策法规，为科技成果转化工作消除体制上的障碍，使经济走上创新驱动的轨道。

[1]Wahab SA,Rose R C,Osman S W.Empirical investigation on the effects of inter-firm technology transfer characteristics on degree of inter-firm technology transfer:a holistic model[J].Asian Social Science,2012,8(1):89-104.

[2]Anderson T R,Daim T U,Lavoie F F.Measuring the efficiency of university technology transfer[J].Technovation,2007,27(5):306-

318.

[3]Jiang Z S.Research on Efficiency of Knowledge Transfer in Technical InnovationAlliances[J].Physics Procedia,2012,25:1947-1954.

[4]徐晨,邵云飞.基于DEA的科技成果转化绩效评价研究[J].电子科技,2010,23(7):58-61.

[5]刘家树,菅利荣.科技成果转化效率测度与影响因素分析[J].科技进步与对策,2010,27(20):113-116.

[6]杨宏进,刘立群.基于三阶段DEA的高校科技创新绩效研究[J].科技管理研究,2011(9):104-107.

[7]CharnesA,Cooper WW,Rhodes E.Measuring the efficiency of decision making units[J].European Journal of Operational Research,1978,2(6):429-444.

[8]Battese G E,Coelli T J.Frontier production functions,technical efficiency and panel data:with application to paddy farmers in India[J].Journal of ProductivityAnalysis,1992,3(2):321-337.

[9]Reinhard S,Lovell K,Thijssen G.Environmental efficiency with multiple stochastic frontier and DEAmethods[J].Applied Economies,2000,32(4):1665-1673.

[10]Kodde DA,Palm F C.Wald criteria for jointly testing equality and inequality restrictions[J].Econometrica,1986,54(5):1243-1248.