考虑桩－土－结构相互作用的桥梁桩基地震反应有限元分析

张 彬，董齐蕾，尹 丹

(辽宁工程技术大学土木与交通学院，辽宁阜新 123000)

0 引言

近几年来，全世界范围内的地震频繁发生，不仅给社会造成极其严重的经济损失，而且还会造成人员伤亡。桩基灾害已经成为桥梁震害主要形式之一，因此，在桥梁设计中更应加强对桩基的考虑。本文以实际工程为例，借助有限元软件分析计算，分析了在地震荷载作用下的桩—土—结构相互作用的桥梁桩基的反应，根据模拟结果分析，对桩基设计提出更为合理的建议。

1 桩-土-结构模型与分析方法

1.1 土体的本构模型

基于Drucker-Prager屈服准则的弹塑性本构模型对于土体弹塑性动力分析效果好，因此，本文采用DP模型作为土体模拟的本构模型。在实际工程中桩体承受的荷载以竖向荷载为主，所以将桩体等效为单一材料。

1.2 动力方程

在地震动输入的桩一土一结构体系任意时刻t的运动方程为:

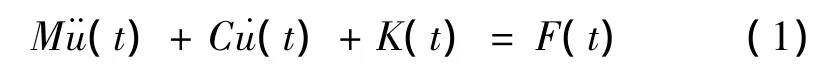
式中，M为系统的质量矩阵;C为阻尼矩阵;K为刚度矩阵;F(t)为结点荷载向量;¨u(t)、˙u(t)、u(t)分别表示系统的结点加速度、结点速度向量和结点位移向量。

本文采用New-mark法进行分析。假设时间间隔Δt内加速度呈现线性变化，在此基础上进行积分，得到t+Δt时刻的位移和速度向量，用位移函数描述位移和速度向量，代入方程，得出时程的反应方程，即:

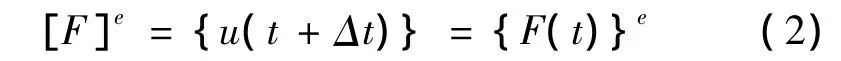
只要知道t时刻的Δt时刻的即可计算出下一时刻各状态的向量。由大量的研究结果表明:当γ≥0.5，β≥0.25时，New-mark法是无条件稳定的。在结构动力分析中，通常取γ=0.5，β=0.25即可取得很好的计算结果［1］。

1.3 地震反应分析方法

动态时程分析法充分考虑了结构的材料属性、几何形状、边界连接条件等非线性因素，还考虑了桩—土—结构相互作用以及地震时程相位差等问题，并且可以直观地反映出地震动的振幅、频谱特性和持续时间，因此，本文采用动态时程分析法［2］。

2 工程实例分析

2.1 工程概况

位于赤峰市内某桥全长632m，宽28m，上部结构为变截面预应力混凝土连续箱梁，下部结构主墩采用11.65m×2m钢筋混凝土八边形桥墩(单幅)，承台厚度2m，主墩桩基采用12根直径为1.2m的钻孔灌注桩，按嵌岩桩进行设计［3］。该区地震烈度为Ⅶ度，地震动峰值加速度0.15g，地震分组为第一组。土层参数见表1。

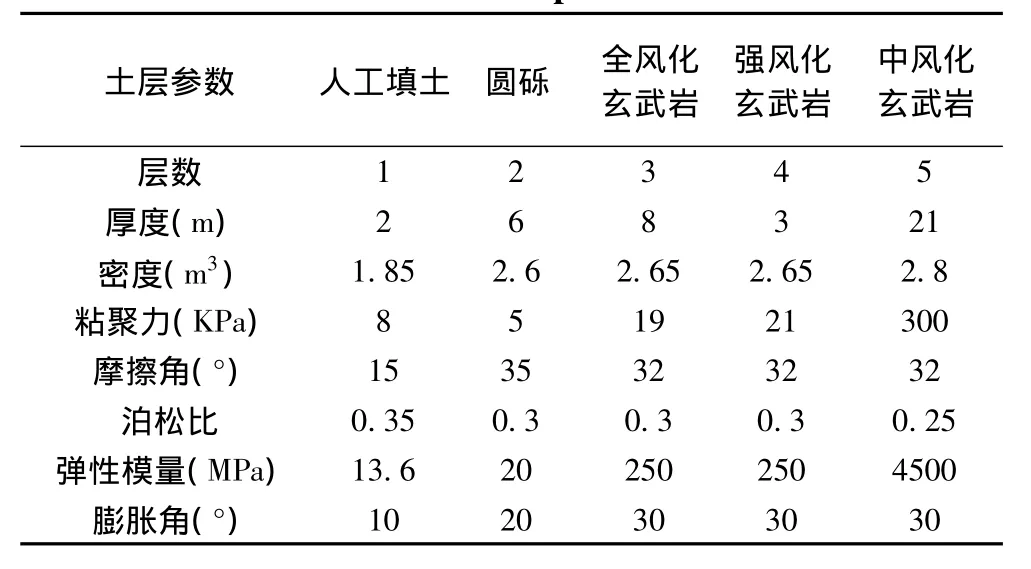
表1 1土层参数Table 1 1 Soil parameters

2.2 地震荷载下桩－土－结构体系影响分析

2.2.1 模型建立

结合上表中的参数，采用3D实体单元进行建模。分别在模型的顶面(上表面)设置应力边界条件;将X，Y方向约束施加在模型的前后和左右四个侧表面上;在底面施加 Z方向约束。模型划分为4371个节点，7个单元组，20174个3D实体单元，如图 1 所示［4］。

图1 有限元模型Fig.1 Finite element model

2.2.2 地震波的选取

本文选取El Centro波，宁河地震天津波和taft波作为地震波的研究波形。

根据国家地震局批准的烈度表，当基本烈度为7度时，地面运动的最大水平加速度a为0.15g，为了简化计算，只截取了部分时段的地震波:取taft波15～25s加速度波(以下简称时程波1);天津波20～30s加速度波(以下简称时程波2);El Centro波10～20s加速度波(以下简称时程波3)。本文中每隔0.2s取一值，共50个。

2.2.3 地震荷载作用下桩-土-结构沉降位移分析

由于在t=13时间步各时程波效果比较好，规律相对比较明显，将此时间步的时程波输入到ADINA软件中可以得到较为规律的点，因此选择t=13时间步进行分析。

将各时程波作用下t=13时间步桩体沉降位移，桩顶各时间步沉降位移总结成图，如图2、图3所示。

图2 各时程波桩体沉降位移Fig.2 Each history wave pile top Settlement displacementdynamic state time dependent

图3 各时程波桩顶沉降位移动态时程Fig.3 Each history wave settlement of pile top displacement dynamic state time dependent

由图2所示，桩体的沉降位移随着桩体的入土深度的变化而变化，桩顶处的沉降位移比桩身其他位置要大，受Z方向约束影响，在土层底部的持力层沉降位移减小趋于零。由图3所示，各时程波作用均会产生不同的沉降位移，具体的位移值由时程波震动的大小的不同而不同，产生的浮动基本与所输入体系地震波震动相关。时程波1作用下沉降位移值在0.07254～0.08476m区间浮动;时程波2作用下沉降位移值在0.07496～0.07685m区间浮动;时程波3作用下沉降位移值在0.07496～0.07701m区间浮动。

2.2.4 桩侧摩阻力

将各时程波作用下t=13时间步桩侧摩阻力，桩顶各时间步桩侧摩阻力总结成图，如图4、图5所示。

图4 各时程波桩侧摩阻力Fig.4 Each history wave pile side of drag

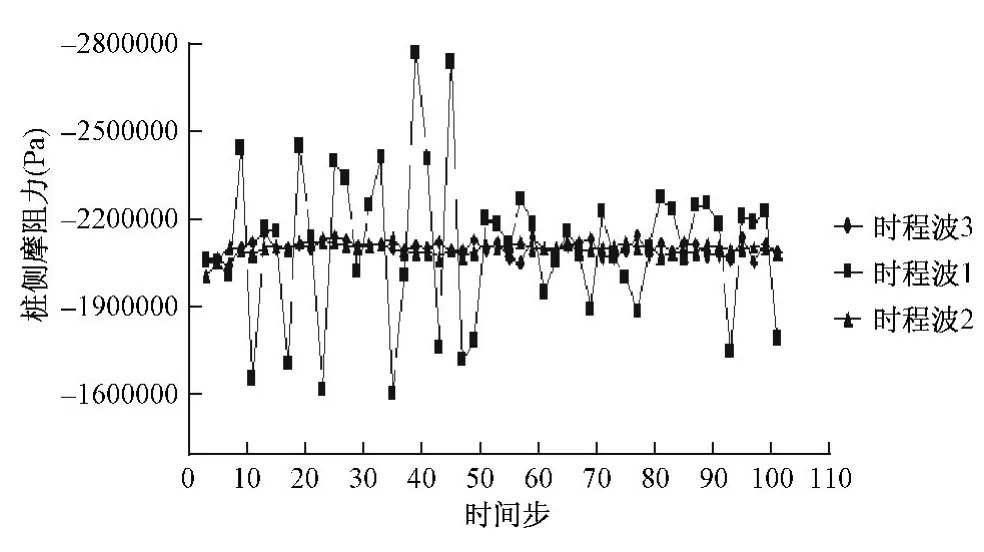
图5 各时程波桩侧摩阻力动态时程Fig.5 Each history wave pile side of drag dynamic state time dependent

由图4、图5可知，由于受承台影响，桩顶附近的侧摩阻力相对较小，随着桩体入土深度的增加，侧摩阻力先在Z轴负向增加，在14m处附近的中硬岩层底部达到最大值，随后侧摩阻力向Z轴正方向增加，负侧摩阻力减小，在20m附近达到中性点，随后增加为正向侧摩阻力，侧摩阻力值的变化基本符合侧摩阻力曲线。不同时程波对桩侧摩阻力均产生影响，不同的时程波引起同一深度处的侧摩阻力值在不同时间步产生浮动，浮动值与时程波的震动规律基本相符。

2.2.5 有效应力

将各时程波作用下t=13时间步桩侧摩阻力，桩顶各时间步桩周有效应力总结成图，如图6、图7所示。

图6 各时程波桩周有效应力Fig.6 The history wave piles week effective stress

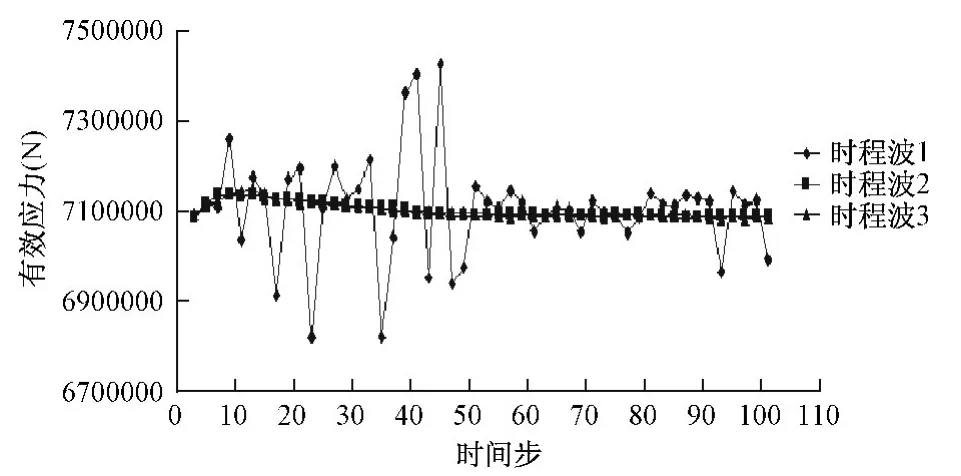
图7 各时程波桩周有效应力动态时程Fig.7 Each the history wave piles week effective stress dynamic state time dependent

从图6、图7可以看出，桩体受土体的有效应力基本按照土层变化及入土深度递减，在桩顶附近的有效应力值比较大，随着各土层中的入土深度的增加，有效应力略有减小，呈曲线变化;在各土层相接处，有效应力会有突变的现象，这是由于各土层的弹性模量、粘聚力、密度等性质的变化，有效应力的变化因此受到影响。在桩顶面的有效应力浮动值基本符合时程波震动规律，但是不同的地震时程波作用的有效应力值不同。

3 结论

本文以位于赤峰市内的某桥梁工程为例，建立了符合工程实际的近似简化模型，通过对模拟结果的分析，在地震荷载作用下桥梁桩体设计时，需考虑桩-土-结构相互作用的影响，应注重以下方面:

(1)桩顶面与承台相接处及其附近的应力及沉降位移的验算;

(2)各土层有明显分层改变处的应力值及沉降位移等参数验算;

(3)应力突变处及有转折处的除应力值外的其他参数验算。

［1］肖晓春，迟世春.水平地震下土—桩—结构相互作用简化分析方法［J］.大连理工大学学报，2003，35(5):561-564.XIAO Xiaochun，CHI Shichun.Horizontal seismic Soilpile-structure interaction analysis method to simplify［J］.Dalian University of Technology，2003，35(5):561-564.

［2］吴正平.引入摩擦元模拟桩土共同作用［J］.南昌航空工业学院学报，2000(4):63-68.WU Zhengping，Introducing friction element modeling of pile-soil interaction ［J］. Nanchang Institute of Aeronautical Technology，2000(4):63-68.

［3］赤峰市新华步行街桥梁设计说明书［R］.辽宁北四达交通技术发展有限公司，2011.Chifeng City，Xinhua Street Bridge Design Manual［R］.Liaoning North Fourth ofTransportation Technology Development Co.，Ltd，2011.

［4］张向东，代丹，许红飞.基于ADINA模拟的桩土相互作用有限元分析［J］.山西建筑，2008，34(36):19-20.ZHANG Xiangdong，DAI Dan，XU Hongfei.ADINA simulation based on finite element analysis of pile-soil interaction［J］.Shanxi Architecture，2008，34(36):19-20.

［5］郑海荣.桩一土一结构相互作用体系的地震响应［J］.地震学刊，1992(2):65-69.ZHENG Hairong.Pile-soil-structure interaction system seismic response［J］.Seismology Journal，1992(2):65-69.

［6］李旭.地震荷载作用下桩—土—上部结构作用机理及数值模拟［D］.西安:华西大学，2010.LI Xu.Pile under earthquake load-soil-Superstructure mechanism and numerical simulation［D］.Xi'an:West University，2010.

［7］W.H.Wu，H.A.Smith.Efficient Modal Analysis for structures with soil-structure interaction Earthquake Engineering and Structure Dynamic，1995，24(3):283-299.

［8］李洞明.地震作用下桩土相互作用的研究与分析［D］.上海:同济大学，2005.LI Dongming.Pile interaction under seismic research and analysis［D］.Shanghai:Tongji University，2005.

［9］毕志成，吴碧中，陈雪丹.桩—土—桩相互作用分析［J］.低温建筑技术，2008(1):107-109.BI Zhicheng，WU Bizhong，CHEN Xuedan.Pile-soil-pile interaction analysis［J］.Low Temperature Architecture Technology，2008(1):107-109.

［10］刘勇生.桥梁结构抗震研究的文献综述［J］.世界地震工程，1992，10(1):48-55.LIU Yongsheng.Bridge seismic research literature review［J］.World Earthquake Engineering，1992，10(1):48-55.

［11］刘立平.水平地震作用下桩—土—上部结构弹塑性动力相互作用分析［D］.重庆:重庆大学，2004.LIU Liping.Pile under horizontal seismic-soil-plastic superstructure dynamic interaction analysis［D］.Chongqing:Chongqing University，2004.

［12］马建.地震作用下桩一土一结构相互作用的分析［J］.科技信息，2011，(8):788-789.MA Jian. Earthquake apileunderasoil-structure interaction analysis［J］. Science and Technology Information，2011，(8):788-789.

［13］范立础.桥梁抗震［M］.上海:同济大学出版社，1997.FAN Lichu.Bridge seismic［M］.Shanghai:Tongji University Press，1997.