基于实测地磁数据仿真的插值算法适构性分析

于运治，姜 璐，田茂均

(海军潜艇学院，山东 青岛 266044）

基于实测地磁数据仿真的插值算法适构性分析

于运治，姜 璐，田茂均

(海军潜艇学院，山东 青岛 266044）

地磁数据具有结构性质多样性，使得对于地磁数据插值的研究在不同区域往往得到不同结论。针对此情况，本文提出插值算法的适构性概念，并建立基于统计学指标的算法适构性评价体系。根据实测地磁数据变化剧烈程度的不同划分5个实验区域;通过等间隔采样的方式，从原始数据中抽取大间隔数据作为实验数据，然后算法插值得到估值数据;围绕原始数据与估值数据残差的集中趋势、离散程度和分布形态等因子，建立基于统计学指标的算法评价体系;仿真验证3种较优插值算法的效果。通过对仿真结果的定量分析，得出了3种插值算法的适构性结论。

地磁图;插值算法;统计学指标

0 引言

地磁数据和其他空间数据一样，结构性质具有多样性。因此，地磁数据的插值很难找到一种插值算法适用于所有情况，学者们在这方面的研究结果佐证了这一点。例如张维娜等学者的研究指出改进的谢别得法非常适用于地磁图插值重构［1］。但黄学功等学者的研究认为径向基函数法更适合于其所研究区域的地磁图构建［2］;而对于克里金插值法及其衍生模型的研究就更多见。这些都说明对于不同的研究区域，由于研究的地磁要素和区域地磁数据空间结构性质的不同，研究得出的结果往往也不尽相同。

由此看来，只研究某一类型区域的最优插值算法，对于插值加密构建地磁匹配基准图还是不够，因为它很有可能在其他性质相异区域得不到如预想的效果。总的来说，对多种类型区域分别验证数种插值算法的效果，最终评价得出各种插值算在不同地磁数据情况中的效果十分必要。针对这一需要，这里提出了插值算法的适构性概念。其中，插值算法适构性是指:插值算法对地磁图插值构建的适应能力，地磁基准图的实测法构建以最大限度的接近自然真值为目的，而插值算法的插值反演以最大限度接近实测值为宗旨。文章围绕评价各插值算法的适构性展开，最后定性得出各类型区域的最优插值算法。

1 算法原理

插值算法在许多工程领域都得到了大量运用，典型的如最小曲率法、样条函数法、多元回归法、数据度量法等［3－4］。而在地理数据的插值研究中，反距离加权法、改进的谢别得法、克里金法、径向基函数法、局部多项式法、自然邻点法等的应用则较为普遍［5］。经过笔者前一阶段的研究发现克里金法、径向基函数法、局部多项式法在海洋地磁数据的插值处理中有较好的表现，本文插值算法适构性的分析即针对这3种方法而展开。

1.1 克里金法

克里金 (Kriging）插值法是一种空间自协方差最优内插算法，实质是利用区域化变量的原始数据和变异函数的结构特点，对未知样点进行线性无偏、最优估计。它一方面通过距离对已知样本点赋权重来计算未知点的值;另一方面又通过变异函数的引入来考虑已知点与未知点的空间关系。克里金法常采用的变异函数模型有常数模型、指数模型、球状模型、高斯模型等［6］。算法原理如下:

对于研究区域A，设在区域内采样的位置坐标为Xi，变量的观测值为 Z(Xi），i=1，2，3，…，n，则预测点X0的估计值Z^(X0）可用这n个样本点的线性组合来表示:

其中λi为已测量点Z(Xi）的权系数。上式中权系数的确定由克里金方程组决定，方程组可表示为:

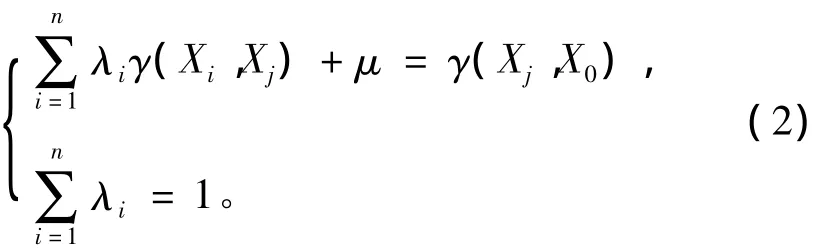
式中:γ(Xi，Xj）为磁测量点的变异函数，μ为拉格朗日系数。本文采用的变异函数为克里金立方模型。

1.2 局部多项式法

多项式插值也是常用的插值方法之一，有着广泛应用。但在进行多项式插值时，要找到一个适合的函数模型不那么容易，而且当多项式的阶数较高时，其波动加大，运算时间也加长。因此，衍生出了局部多项式法 (local polynomial，LP）。局部多项式法是一种局部加权最小二乘方法，即对插值对象给定一搜索域，然后根据适当的特定阶数的多项式函数插值出待插值点的值。局部多项式插值产生的曲面主要依赖于区域化变量的局部变异。其主要采用的多项式有一次、二次和三次多项式［7］。

1.3 径向基函数法

径向基函数法 (radial basis function，RBF）是一种精确的插值方法，适用于对大量点数据进行插值计算，从而获得平滑表面，且能预测比样点高或低的未知点的值，因而具有较高的预测精度，能较好地反应数据变化情况。它首先将插值函数构造成下面形式的空间点函数:

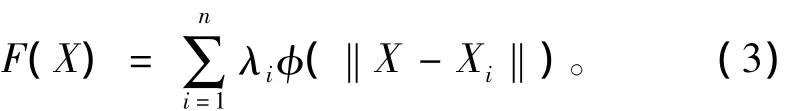
式中:X=(x，y，z），Xi为已知点 (i=1，2，…，n）;λi为待定系数;φ为指定的基函数;‖·‖为欧氏范数。然后权系数的求解可以用已知数据点的值通过插值设定的条件确定。

影响径向基函数法插值精度关键是基函数的确定，常用的有逆二次曲面、二次曲面、自然三次样条、Gauss函数、复二次函数、倒转复二次函数、薄板样条函数［8］。本文采用复二次函数。

2 算法仿真实验

2.1 仿真实验数据

数据来源于某单位在某海区科研课题所采集的磁异常数据。涉及到数据保密性等原因去掉了经纬度而改为绝对距离。为验证算法在不同数据变化区域的效果，依据该区域磁异常变化的剧烈程度确立了5个实验区。其中实验区1数据的特点是变化幅度大，程度相对剧烈;实验区2数据特点是变化幅度较大，程度非常剧烈;实验区3数据则变化幅度小，剧烈程度较弱;实验区4数据变化最为平缓;实验区5是包含上述4个实验区的一个大区，作为不确定数据变化剧烈程度的区域存在。实验区原始数据 (50 m精度）三维图如图1～图4所示。

图1 实验区1磁异常三维图Fig.1 Experimental zone 1 magnetic anomalies in three-dimensionalmap

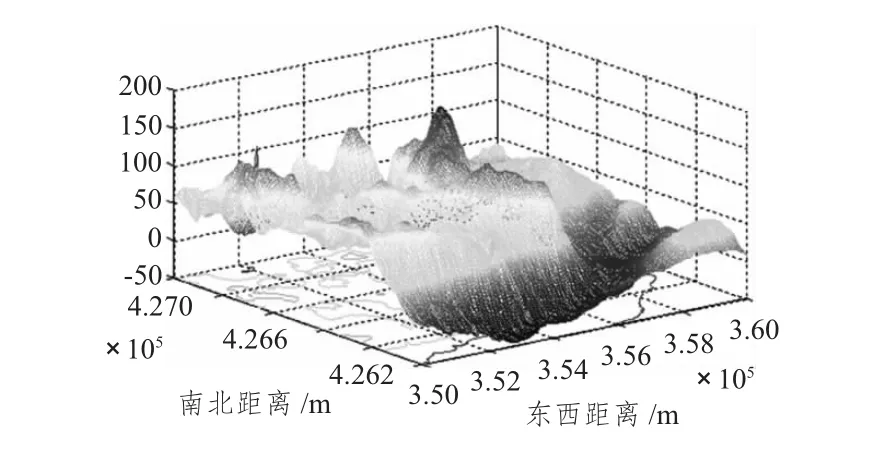
图2 实验区2磁异常三维图Fig.2 Experimental zone 2 magnetic anomalies in three-dimensionalmap

图3 实验区3磁异常三维图Fig.3 Experimental zone 3 magnetic anomalies in three-dimensionalmap

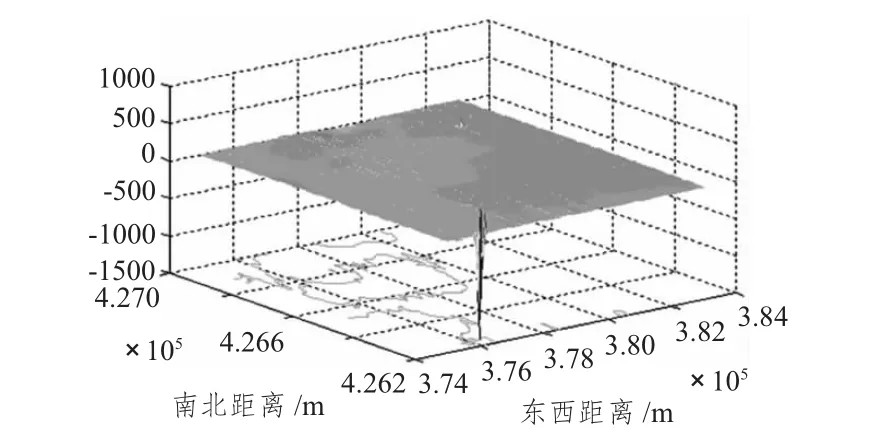
图4 实验区4磁异常三维图Fig.4 Experimental zone 4 magnetic anomalies in three-dimensionalmap

实验区5范围较大，且是综合上述4个区域的综合区，因此不再图示说明。

2.2 算法评价体系

1）评价方法

算法评价是将部分已知属性值的样本点作为“训练数据集”(占原始数据量的1%）用于算法插值计算;将原始所有数据点作为“验证数据集”存在。然后利用“训练数据集”样本点进行插值计算，将得出的插值结果与“验证数据集”中的点测量值对比得出插值算法残差;最后运用各定量评价指标比较各插值算法的适构性。文章采取等间隔采样的方式 (由于目前大部分海上测量都采用的是等间隔）确定等间隔500 m的点作为训练数据集，原始50 m精度的点作为验证数据集。

2）定量评价指标

评价指标确立从2方面考虑，一是算法的运算时间;二是残差的性质。对残差性质的分析目前还是以统计学指标定量评价为主，为此本文从数据集中趋势、离散程度和分布形态3个方面确定均值、平均绝对差、全距、标准差、峰度和偏态等6个统计学指标，再加上运算时间共计7个定量评价指标。指标表示如下［9－10］:

2.3 仿真结果与分析

1）各插值算法仿真验证指标值

各插值算法仿真验证指标值如表1～表5所示。

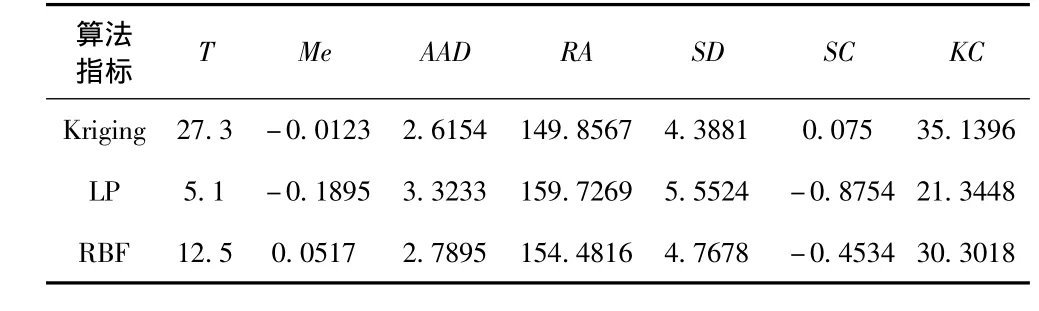
表1 实验区1指标值Tab.1 Experimental zone 1 indicator value table

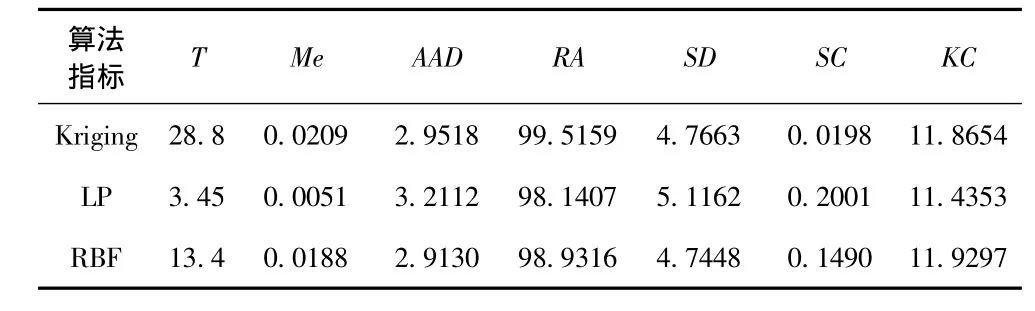
表2 实验区2指标值Tab.2 Experimental zone 2 indicator value table

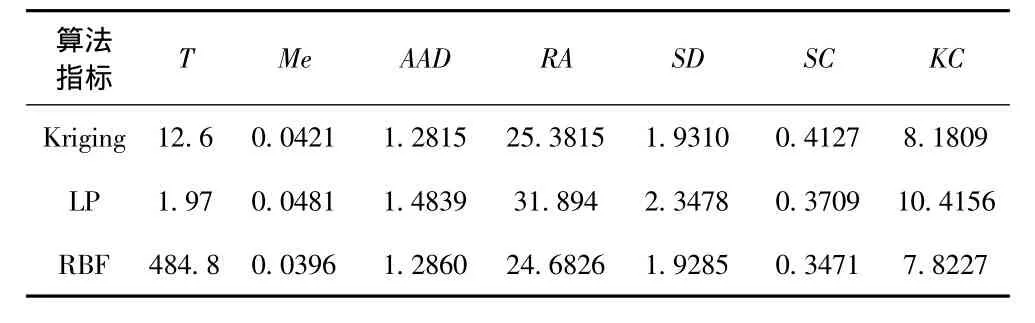
表3 实验区3指标值Tab.3 Experimental zone 3 indicator value table

表4 实验区4指标值Tab.4 Experimental zone 4 indicator value table

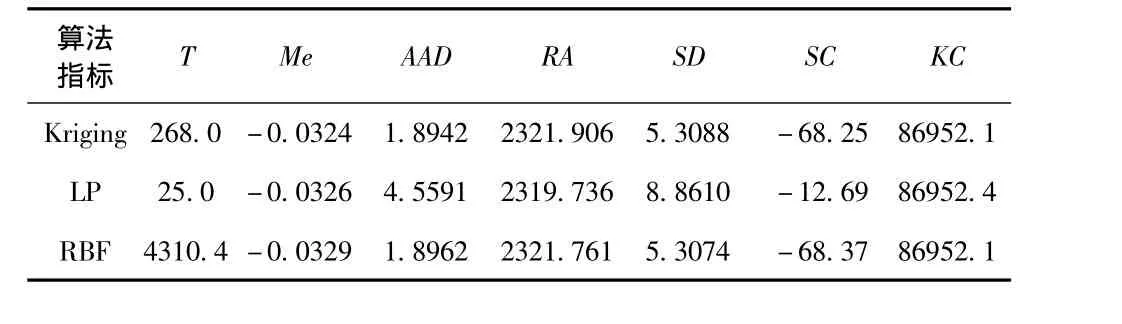
表5 实验区5指标值Tab.5 Experimental zone 5 indicator value table

2）分析结论

从实验区1可看出，克里金法与真值的偏差、数据离散程度、极距等都最小，且分布形态也较为合适，唯一不足的是时效性太差;径向基函数法与克里金法效果接近，而且在时效性上优于克里金法;而局部多项法则在时效性上占了优势。

实验区2结果反映出径向基函数法平均绝对差、标准差、以及运算时间3个重要指标上都占了优势，而且分布形态也较为理想，适构性最好。另外2个次之。

实验区3虽然径向基函数法在绝对差、标准差等重要指标上都最好，但是其时效性太差，而各指标和它接近的克里金法时效性适中，适构性最优。

实验区4中方法的效果除了运算时间外，差别非常小;而参考运算时间来看局部多项式法适构性最佳。

实验区5反映出的结果和实验区3相似，综合来看克里金法适构性优于另外2个。

综合上述5个实验区的分析结果可得出结论;在海洋地磁数据的插值处理中，如果不明确数据变化的剧烈程度应当优先采用克里金法;而明确数据变化程度特别剧烈时应当采用径向基函数法;变化缓慢时优先考虑局部多项式法。

3 结语

由于海洋地磁数据获取的困难性，要获得高精度、高密度的地磁数据非常困难。然而，随着目前地磁匹配导航应用于水下潜航器导航研究的发展。对于地磁图网格精度的要求却在逐渐提高，针对这一矛盾，插值算法的引入是解决困境的关键技术之一。但是插值算法众多，地磁数据的结构特性也各异，因此为选择合适的插值算法给出一定参考准则十分必要。本文研究了3种插值算法在数个地磁变化情况不同区域的效果，以适构性作为算法选取准则的核心做了仿真验证，并得出了克里金法、局部多项式法和径向基函数法的适构性结论。虽然本文的研究取得了一定的成果，但是诸多方面还有待进一步研究。由于海上数据测量的困难性，所能提供的实测数据有限，要更好的评价算法的适构性，就需要大量的实测数据作为实验数据或者佐证数据。这一方面还需要进一步的拓展。

［1］黄学功，房建成，刘刚，等.地磁图制备方法及其有效性评估［J］.北京航空航天大学学报，2009，35(7）:891－894.

HUANG Xue-gong，FANG Jian-cheng，LIU Gang，et al.Geomagneticmapping and validity estimation［J］.Journal of Beijing Universiy of Aeronautics and Astronautics，2009，35(7）:891－894.

［2］张维娜，吕云霄，吴美平.改进谢别德插值方法在地磁图构建中的应用［J］.导航与控制，2011，2(10）:28－32.

ZHANGWei-na，LV Yun-xiao，WU Mei-ping.Application ofmodified shepard interpolation in geomaglletic map［J］.Navigation and Control，2011，10(2）:28 －32.

［3］乔玉坤，王仕成，张金生，等.区域地磁场建模主要方法及其在地磁导航基准图构建中的应用［C］.第五届国家安全与军事地球物理学术研讨会论文集，2009.

QIAO Yu-kun，WANG Shi-cheng，ZHANG Jin-sheng.Regional geomagnetic field modeling method and its geomagnetic navigation reference map building［C］.Conference Proceedings of the Fifth National Security and Military Geophysical，2009.

［4］王哲，王仕成，张金生，等.一种地磁匹配制导基准图制备方法及其有效性评价［J］.系统工程与电子技术，2008，30(11）:2207 －2211.

WANG Zhe，WANG Shi-cheng，ZHANG Jin-sheng，et al.Method for preparation of reference map in geomagnetism matching guidance and its validity evaluation［J］.Systems Engineering and Electronics，2008，30(11）:2207 －2211.

［5］朱会义，刘述林，贾绍凤.自然地理要素空间插值的几个问题［J］.地理研究，2004，23(4）:425 －432.

ZHU Hui-yi，LIU Shu-lin，JIA Shao-feng.Problems of the spatial interpolation of physical geographical elements［J］.Geographical Research，2004，23(4）:425 －432.

［6］白世彪，王建，常直杨.Surfer10地学计算机制图［M］.北京:科学技术出版社，2012:217－220.

BAI Shi-biao，WANG Jian，CHANG Zhi-yang.Surfer10 geoscience computer graphics［M］.Beijing:Science and Technology Press，2012:217 －220.

［7］汪俊，高金耀，吴招才，等.局部多项式插值方法在多源海底沉积厚度数据融合中的应用［J］.海洋科学，2009(4）:25－28.

WANG Jun，GAO Jin-yao，WU Zhao-cai，et al.The local polynomials fitting methods on geospatial data merging:an application to the multi-resources marine sediment thickness data［J］.Marine Sciences，2009(4）:25 － 28.

［8］缪报通，陈发来.径向基函数神经网络在散乱数据插值中的应用［J］.中国科学技术大学学报，2001，31(2）:135－142.

MIAO Bao-tong，CHEN Fa-lai.Applications of radius basis function neural networks in scattered data interpolation［J］.Journal of University of Science and Technology of China，2001，31(2）:135 －142.

［9］贾俊平，何晓群，金勇进.统计学［M］.北京:中国人民大学出版社，2000:212－219.

JIA Jun-ping，HE Xiao-qun，JIN Yong-jin.Statistics［M］.Beijing:China Renmin University Press，2000:212 －219.

［10］杜智敏.抽样调查与SPSS应用［M］.北京:电子工业出版社，2010:471－485.

DU Zhi-min.Sample survey and SPSS applications［M］.Beijing:Publishing House of Electronics Industry，2010:471－485.

［11］王孝玲.教育统计学(2版）［M］.上海:华东师范大学出版社，2001:290－307.

WANG Xiao-ling.Educational statistics(2 edition）［M］.Shanghai:East China Normal University Press，2001:290－307.

Analysis of interpolation suitability of algorithm based on simulation of themeasured geomagnetic data

YU Yun-zhi，JIANG Lu，TIAN Mao-jun
(Navy Submarine Academy，Qingdao 266044，China）

The structural properties diversity of the geomagnetic data，make for geomagnetic data interpolation research in different areas often get different conclusions.In view of this situation，this paper puts forward the optimal structure concept of the interpolation algorithm，and to establish the interpolation suitability of algorithm evaluation system based on the statistical indicators.Firstly，the paper based on different change intensity of the geomagnetic data has division of the five experimental area;Secondly，through the way such as sampling interval，extract big interval data from the original data as experimental data，and use the interpolation algorithm gets valuation data;Thirdly，around the original data and valuation data residual concentration trend，discrete degree and distribution form factors，this paper build the interpolation suitability of algorithm evaluation system based on statistics index;Finally，take advantage of simulation results show the effectof three better interpolation algorithm.Based on the quantitative analysis of the simulation results，it is concluded that interpolation suitability of algorithm conclusion of the three kinds of interpolation algorithm.

geomagnetic mapping;interpolation method;statistical indicators

U666.1

A

1672－7649(2014）05－00130－05

10.3404/j.issn.1672－7649.2014.05.027

2013－01－29;

2013－03－18

于运治(1964－），男，高级工程师，主要从事潜艇导航方面研究。