低渗透油藏长缝压裂直井稳态产能预测模型
2014-03-06刘慧卿吕广忠
王 锋,刘慧卿,吕广忠
(1.中国石化胜利油田分公司技术发展处,山东东营257000;2.中国石油大学(北京)石油工程学院,北京102249;3.中国石化胜利油田分公司地质科学研究院,山东东营257015)
低渗透油藏长缝压裂直井稳态产能预测模型
王 锋1,2,刘慧卿2,吕广忠3
(1.中国石化胜利油田分公司技术发展处,山东东营257000;2.中国石油大学(北京)石油工程学院,北京102249;3.中国石化胜利油田分公司地质科学研究院,山东东营257015)
低渗透油藏长缝压裂直井已在现场获得广泛应用,但目前仍缺乏适用于其工程应用的快速、准确的产能预测模型。为此,根据低渗透油藏长缝压裂直井周围地层渗流情况,运用保角变换原理与双线性渗流理论,建立了低渗透油藏压裂裂缝无限与有限2种导流能力下、考虑启动压力梯度长缝压裂直井稳态产能预测模型,通过与现场实例对比验证了模型的准确性,并利用该产能预测模型计算绘制了油井IPR曲线,分析了裂缝参数对长缝压裂油井产能的影响。结果表明:新建产能预测模型与现场实例基本相符,误差均小于9%,说明模型的准确性较高;长缝压裂直井压裂缝长对产能的影响程度大于裂缝导流能力对产能的影响;当压裂缝长一定时,长缝压裂直井裂缝存在最佳导流能力。
低渗透油藏长缝压裂启动压力梯度无限导流能力有限导流能力稳态产能
在低渗透油藏开发过程中,由于其储层具有渗透率低、孔隙小的特点,大量生产井须通过压裂改造,油井周围地层的渗流情况得到改善后,才能获得较好的开发效果。近年来,中外学者采用多种方法研究了低渗透油藏压裂井的产能预测模型[1-12],主要包括考虑启动压力梯度或非达西渗流的椭圆流模型和线型流模型,但存在考虑因素简单或简化模型缺乏合理性的问题。为此,笔者综合前人研究成果,推导了在低渗透油藏中考虑启动压力梯度的长缝压裂直井的双线性流模型,并利用保角变换方法[13],对压裂裂缝无限导流能力与有限导流能力2种情况下的稳态产能理论进行了研究,以期为低渗透油藏长缝压裂直井产能预测评价提供依据。
1 模型的建立
低渗透油藏长缝压裂直井稳态产能预测模型的基本假设包括:①裂缝高度与油层有效厚度相等;②裂缝宽度远小于原油供给半径;③裂缝导流能力分为无限导流和有限导流2种情况;④流体渗流为单相渗流;⑤稳态渗流,只考虑水平方向流动;⑥忽略地层及裂缝污染。
利用保角变换,将图1中z平面中的各点进行一一映射,得到ω平面,即宽度为d的带状地层,z平面中的压裂裂缝AB映射为ω平面中A′B′,z平面中的井筒o映射为ω面中o′,将裂缝井中流体的渗流等效为在长度为he、宽度为d的横截面内由o″向A′B′的单向渗流。其保角变换公式为

式中:z为z平面内的复变函数;xf为裂缝半长,cm;ω为ω平面内的复变函数。
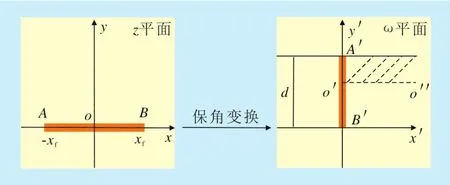
图1 低渗透油藏长缝压裂直井保角变换示意
x为ω平面内流动等势线的横坐标,cm;y为ω平面内流动等势线的纵坐标,cm;d为ω平面内裂缝宽度,cm;x′为渗流长度,cm;y′为裂缝微元体长度,cm
当裂缝导流能力无限大时,结合达西公式,可得压裂直井的产能为

式中:Q为压裂直井的产能,cm3/s;Hf为裂缝高度,cm;K0为地层有效渗透率,μm2;μ为地层流体粘度,mPa·s;p为压力,MPa;G为启动压力梯度,MPa/cm。
对式(2)积分后可得
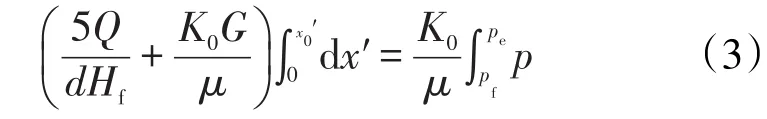
式中:x0′为ω平面内供给半径,cm;pe为供给半径处压力,MPa;pf为裂缝处压力,MPa。
当x0′为常数时,根据保角变换原理,可得流动等势线方程为
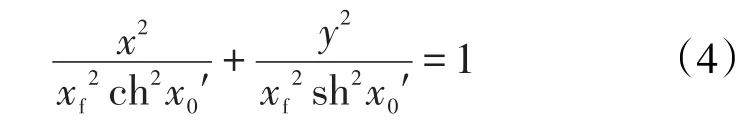
在工程应用误差允许范围内,式(4)中的chx0′和shx0′可分别近似为

将式(5)和式(6)代入式(4),可得
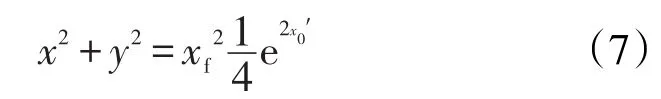
z平面内供给半径可表示为

式中:re为z平面内供给半径,cm。
由式(7)和式(8)可得

将式(9)代入式(3)并整理,得到考虑启动压力梯度的无限导流能力垂直裂缝井产能计算式为
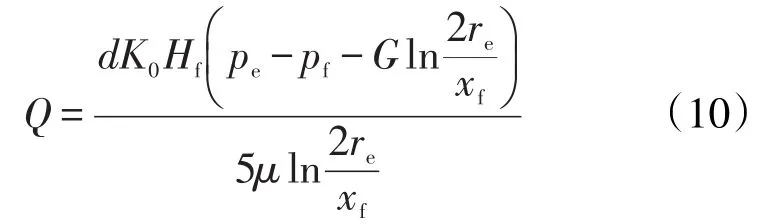
对于考虑启动压力梯度的有限导流能力垂直裂缝井,先对ω平面内长度为dy′的矩形裂缝微元体进行讨论。平面内微元体两侧流体的流入和流出速度分别为
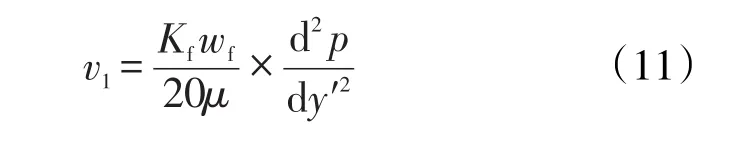

式中:v1为流体流入微元体时的渗流速度,cm/ s;Kf为裂缝有效渗透率,μm2;wf为裂缝宽度,cm;v2为流体流出微元体的渗流速度,cm/s;p0为油层静压,MPa。
根据质量守恒定律,流出单元与流进单元的质量相等,忽略流体压缩性,联立式(11)和式(12),可得

式中:pw为井底压力,MPa。
由式(13)可得
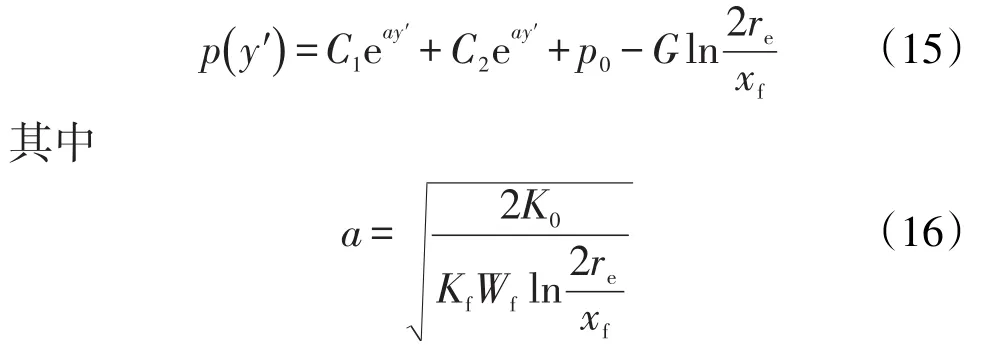
式中:p(y′)为微元体处的压力,MPa;C1和C2为待定参数。
联立式(14)和式(15),可得
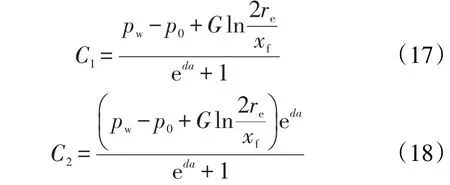
原油在裂缝内的流动符合达西定律,可得考虑启动压力梯度的裂缝有限导流能力长缝压裂井产能公式为
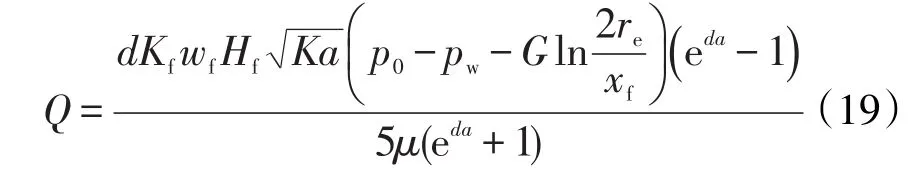
2 模型准确性验证
樊142区块是夹于大套油页岩中、厚度为5~16 m的浊积砂岩特低渗透原生油藏,其相关参数基础数据包括:供给半径为350 m,储层有效渗透率为1.5×10-3μm2,井筒半径为0.1 m,油层厚度为10 m,地层原油粘度为3.54 mPa·s,油层静压为42 MPa,启动压力梯度为0.5 MPa/m。
从表1可以看出,3口压裂井实际平均产能与式(19)的计算结果基本吻合,误差小于9%,符合工程应用误差要求。

表1 压裂井实际产能与预测结果对比
3 产能影响因素分析
利用实例数据,绘制IPR曲线,分析裂缝参数对产能的影响。当裂缝半长为170 m时,由不同裂缝导流能力下油井的IPR曲线(图2)可以看出:油井压裂后的产能较压裂前有大幅度提高;在裂缝缝长保持不变的条件下,当裂缝导流能力由30×10-3μm2·m增至300×10-3μm2·m时,油井的IPR曲线斜率受裂缝导流能力的影响较小。
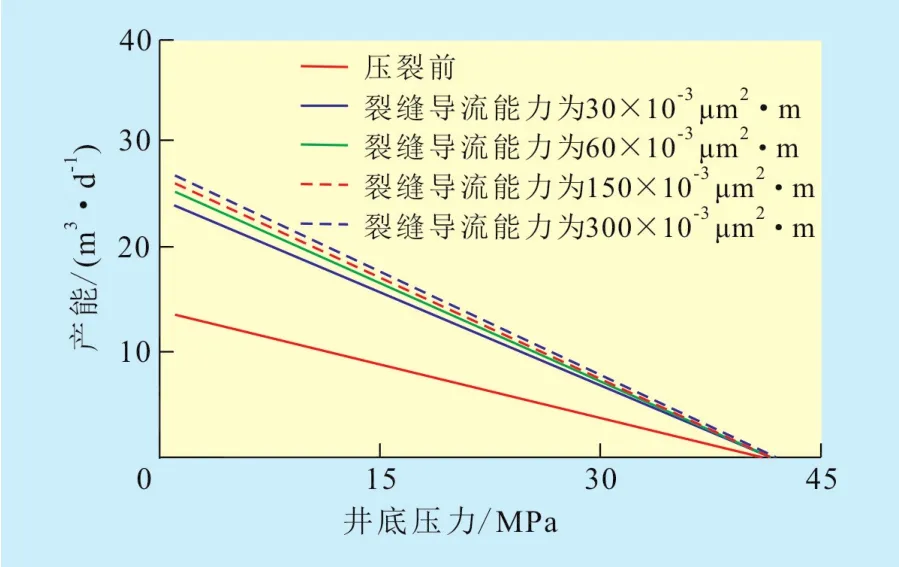
图2 不同裂缝导流能力下油井的IPR曲线
当裂缝导流能力为300×10-3μm2·m时,不同裂缝半长下油井的IPR曲线(图3)表明:压裂后油井产能大幅度提高,同时当裂缝导流能力不变时,油井的IPR曲线斜率受裂缝缝长的影响较大,油井产能随裂缝半长的增加而大幅度增加。说明裂缝缝长对产能的影响程度大于裂缝导流能力对产能的影响程度。
当裂缝导流能力为300×10-3μm2·m、裂缝半长为70 m时,不同地层有效渗透率下油井的IPR曲线(图4)表明:地层有效渗透率对油井产能和油井的IPR曲线斜率影响均较大,油井产能随地层有效渗透率的增加而大幅度增加。
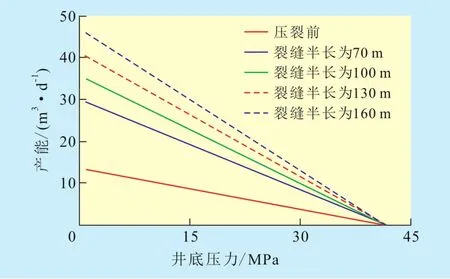
图3 不同裂缝半长下油井的IPR曲线

图4 不同地层有效渗透率下油井的IPR曲线
4 结论
在考虑启动压力梯度的条件下,推导了低渗透油藏无限导流能力垂直压裂井与有限导流能力垂直压裂井的稳态产能公式。现场实例表明,该产能预测模型计算准确率较高。
结合裂缝有限导流能力的长缝压裂直井的稳态产能计算公式,计算并绘制了油井的IPR曲线。通过IPR曲线分析可知:长缝压裂裂缝缝长对产能的影响程度大于裂缝导流能力对产能的影响程度,同时在长缝压裂直井裂缝缝长一定的条件下,裂缝存在最佳导流能力。
[1] 何逸凡,廖新维,徐梦雅,等.低渗透气藏压裂水平井产能预测模型及其应用[J].油气地质与采收率,2012,19(4):93-96.
[2] 蒋廷学,单文文,杨艳丽,等.垂直裂缝井稳态产能的计算[J].石油勘探与开发,2001,28(2):61-63.
[3] 姚志良,曹飞,丁士东,等.分支井产能预测模型及分支形态优化[J].油气地质与采收率,2013,20(3):56-59.
[4] 何应付,徐联玉,吕万一,等.低渗透气藏压裂井产能分析[J].特种油气藏,2006,13(5):59-60.
[5] 汪永利,蒋廷学,曾斌,等.气井压裂后稳态产能的计算[J].石油学报,2003,24(4):65-68.
[6] 邴绍献.油田单井可采储量定量预测模型[J].油气地质与采收率,2013,20(1):85-88.
[7] 李生,李霞,曾志林,等.低渗透油藏垂直裂缝井产能评价[J].大庆石油地质与开发,2005,24(1):54-56.
[8] 尹洪军,刘宇,付春权,等.低渗透油藏压裂井产能分析[J].特种油气藏,2005,12(2):55-56.
[9] 张德良,张烈辉,赵玉龙,等.低渗透气藏多级压裂水平井稳态产能模型[J].油气地质与采收率,2013,20(3):107-110.
[10]刘慈群.双重孔隙介质中有限导流垂直裂缝井的非牛顿流体试井分析方法[J].石油学报,1990,11(4):61-67.
[11]黄延章.低渗透油层渗流机理[M].北京:石油工业出版社,1997.
[12]陈德民.有限导流垂直裂缝井稳态渗流解析解及产能分析[J].大庆石油地质与开发,2006,13(4):62-64.
[13]张伟东,杨铁军,蒋廷学,等.保角变换法用于计算压裂井产能[J].油气地质与采收率,2003,10(增刊):81-82.
编辑常迎梅
TE313.8
:A
1009-9603(2014)01-0084-03
2013-11-03。
王锋,男,高级工程师,博士,从事油田开发方面的科研管理与技术研究。联系电话:(0546)8552322,E-mail:wangfeng755. slyt@sinopec.com。
国家科技重大专项“低渗油气田高效开发钻井优化设计技术”(2011ZX05022-001)。
