基于序列二次规划算法的油藏动态配产配注优化

张 凯，路然然，张黎明，张 龙，姚 军

（1.中国石油大学（华东）石油工程学院，山东青岛266580；2.中国石油塔里木油田分公司天然气事业部，新疆库尔勒841000）

基于序列二次规划算法的油藏动态配产配注优化

张 凯1，路然然1，张黎明1，张 龙2，姚 军1

（1.中国石油大学（华东）石油工程学院，山东青岛266580；2.中国石油塔里木油田分公司天然气事业部，新疆库尔勒841000）

油藏动态配产配注已经成为实现油田效益最大化的有效措施之一。为提高优化运算速度，处理非线性不等式约束，将序列二次规划算法应用到油藏动态配产配注求解过程中。应用序列二次规划算法将求解变量最优值的非线性优化问题转化为一系列的求解变量搜索方向的二次规划子问题，控制变量的搜索方向采用伴随方法和Broy⁃den-Fletcher-Goldfarb-Shanno（BFGS）方法得到，迭代求取控制变量最优值。实例验证结果表明，总注入量等式约束条件下的最优开发方案，累积产油量增加12.8%，累积注水量下降11.1%，累积产水量下降22.3%，含水率下降4.16%；总注入量不等式约束下的最优开发方案，累积产油量增加29.1%，累积注水量下降26.9%，累积产水量下降30.3%，含水率下降4.16%。但是，在不等式约束情况下，由于注采失衡，油藏压力大幅下降，易造成后期开发能量不足；需对总注入量及采出量进行等式约束或在不等式约束的基础上添加约束下限。运用该方法对胜利油区埕岛油田27A区块进行方案调整优化，结果表明，优化后的采出程度相对于优化前提高0.92%，净现值增长35%。

序列二次规划配产配注动态开发等式约束不等式约束

中国主力油区大多数已经进入高含水开发阶段［1-3］，油田稳产难度大。在这种形势下如何提高油田控水稳油效果，高效合理开发油田，是石油行业迫切需要解决的问题［4］。因此，油藏动态配产配注优化技术应运而生。油藏动态配产配注优化是指以计算机模拟技术为基础，综合利用最优化方法［5-6］和理论，对油田生产制度进行优化［7］，以实现开发效益最大化的技术。其优化方法主要有随机算法（如遗传算法［8］、模拟退火算法［9］）和梯度法（如最速下降法［10］和拟牛顿法［10］）2种，后者应用更为广泛。

Fathi等利用伴随梯度算法进行了表面活性剂驱、CO2驱及蒸汽驱优化［11-13］；Zakirov等利用伴随模型对薄互层油藏进行了生产优化［14］；Zakirov等利用伴随算法，对水驱油藏闭合生产进行了优化研究［15-18］。但这些方法均无法有效解决非线性约束问题（如无法保证优化时间内总注水量一定）。油藏生产问题中控制变量通常需要满足一定的约束条件，包括等式约束、不等式约束以及边界约束等［19］。Bieker等利用罚函数法与Karush-Kuhn-Tucker条件混合来处理约束条件［20］；Sarma等采用近似可行方向法来处理非线性不等式约束［21］，Lien等采用梯度平衡方法研究了约束优化［22］。然而上述方法求解速度慢，且不能实现精确约束。为此，笔者将伴随方法与序列二次规划算法（SQP）结合，提出了一种基于SQP方法的油藏动态配产配注优化方法，以期利用序列二次规划超线性收敛的优势及将约束优化求解问题转化为无约束最优化问题求解的特点，实现生产优化约束求解，提高运算效率。

1 数学模型

油藏生产优化通过优化油水井的产出和注入参数，来减缓水的指进，增大原油的采出程度，从而实现油藏目标函数的最大化。油田开发规划一般存在3种不同的目标函数模型［23-26］：①确定规划期各年目标产量后，规划产量构成，追求总成本最低的目标函数模型；②在保持盈亏平衡情况下，寻求最大产量的目标函数模型；③结合产量与成本，综合考虑利润最大化的目标函数模型。笔者以三维三相油藏模拟器来描述油藏开发生产系统，选用第3类目标函数模型，将生产期内经济净现值作为性能指标函数评价注水开发效果，其表达式为

式中：J为生产期内的经济净现值，元；l为总控制时间步；n为控制时间步的迭代次数；Jn为第n次控制时间步内的经济净现值，元；xn+1为第n+1次控制时间步的状态变量（各个网格压力、饱和度和组分等）；sn为第n次控制时间步的控制变量（如油井生产流压及油井流量和注水井注入量等）；Δtn为第n次控制时间步模拟计算时间步，d；tn为至第n次控制时间步的累积计算时间，d；b为平均年利率，%；为总生产井数，口；ro为原油价格，元/ m3；为第 j口生产井第n次控制时间步的平均产油速度，m3/d；rw为产水成本，元/m3；为第 j口生产井第n次控制时间步的平均产水速度，m3/d；Ninj为总注水井数，口；rwi为注水成本，元/m3；为第i口注水井第n次控制时间步的平均注水量，m3/d。

每个模拟时间步，油藏中的剩余油饱和度及压力均会发生改变。根据质量守恒原则，可得油藏数值模拟压力方程为

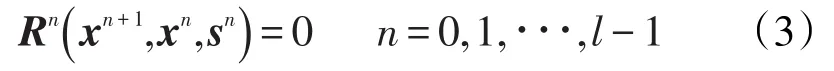
式中：Rn为油藏数值模拟压力函数。

将目标函数与油藏流动方程相结合，使等式约束优化转换为无约束优化，目标函数的增广La⁃grange函数为

式中：JA为目标函数的增广Lagrange函数；λn+1为第n+1次控制时间步的Lagrange乘子。

除了油藏流动方程外，在实际生产中控制变量仍满足一定的约束条件，包括等式约束和不等式约束。区块整体产液量或者注入量可为等式约束也可为不等式约束，其表达式分别为

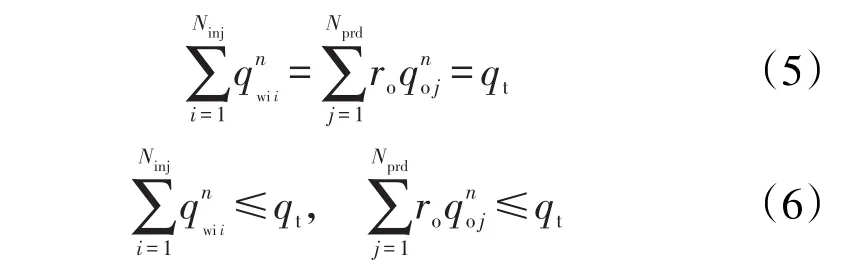
式中：qt为区块整体产液量或者注入量，m3。

边界约束是最常见的不等式约束形式，对于油水井流量控制，其下边界通常设为0，即关井；对于油井井底流压［27］控制，压力下边界一般高于泡点压力或者设定某一合适的值来抑制底水锥进；对于水井井底压力，其上边界一般要低于地层的破裂压力。将各个时间步的控制变量用s来表示，记，将各个时间步的状态变量用x表示，记x=

油藏生产优化就是在控制变量满足各种约束的条件下，求取性能指标的最大值及相应的最优控制变量（主要包括井底流压、油水井流量等）的非线性最优化问题，即

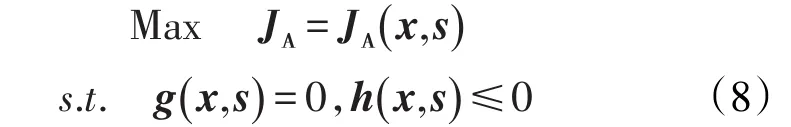
2 优化求解

笔者提出了基于梯度算法的改进序列二次优化算法来求解式（8），该方法须将优化理论与油藏数值模拟结合，求解最优的油藏动态配产配注方案。注采量的变化梯度值使用伴随方法求解，可在参数数量庞大的情况下快速准确地提供目标函数关于控制变量的梯度值。再用SQP算法约束累积注入量及累积产液量，保证一定的注采比。笔者将SQP算法与梯度算法结合，充分利用二者的优势，以提高优化的速度和精度。

2.1 SQP算法简介

SQP算法［28］在动态配产配注过程中，每一次迭代、收敛均可由Lagrange函数的正定Hessen矩阵来保证，Hessen矩阵可通过拟牛顿法得到。使用SQP算法求解非线性约束优化问题比无约束问题进行的迭代次数要少，这是因为约束优化问题的解受约束区域限制，更易得到恰当的搜索方向和迭代步长。

利用式（1）—式（4），构造Lagrange函数为

式中：μ为等式约束的Lagrange乘子向量；v为不等式约束的Lagrange乘子向量。

求解式（9）时，每次迭代油水井的注采量都需满足Karush-Kuhn-Tucker条件，即

将第k次迭代的Karush-Kuhn-Tucker条件关于注采量s(k)进行一阶Taylor展开，即

式（11）表明目标函数和约束条件之间的梯度相互抵消，其中Lagrange乘子(μ(k)，v(k))平衡了优化

目标函数和约束条件之间梯度幅度的差异。由式（8）与式（10）的对应关系可知，式（11）对应的非线性优化问题为

此规划问题中只有Δs(k+1)是未知数，由式（8）求解s的过程转化为式（12）求解Δs(k+1)的过程。沿Δs(k+1)的方向进行线性搜索，得到步长αk，便可更新迭代点s(k+1)=s(k)+αkΔs(k)，修改参数场。不断重复这个过程，直至得到最优控制变量。由于不同的s(k)对应的目标函数的梯度值及Hessen矩阵不同，因此每步s(k)都需要解1个二次规划子问题QP(s(k))。

2.2 伴随梯度的计算

根据油、气、水的流动方程，求得目标函数中生产效益对于注采量的梯度，再代入SQP算法构建的Hessen矩阵，求解约束动态配产配注优化问题。式（12）求解过程中最重要的在于对式（9）求导，得到目标函数对单井注采量的梯度，进而获取油田开发的配产配注方案。利用离散极大值原理，由式（3）可得目标函数的增广Lagrange函数的一阶变分为

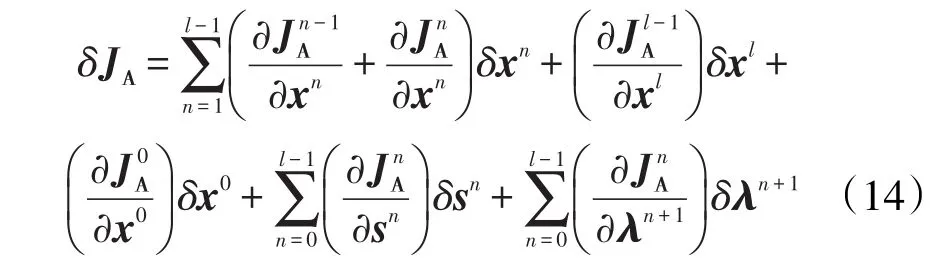
式中：δJA为目标函数的增广Lagrange函数的一阶变分；分别为第n-1， n，l-1，0和n次控制时间步目标函数的增广La⁃grange函数；xl为第l次控制时间步的状态变量；x0为初始时刻的状态变量。

JA取极值的必要条件是δJA=0，且式（14）右边各项相互独立，各项须都等于0。根据式（3）和式（4）可知，=Rn=0；油藏开发时的初始状态已知，故δx0=0；若式（14）其余3项均等于0，则其系数为0。由于相应的Lagrange乘子未知，须先对其进行求解。将式（4）代入式（14）前2项的系数，可得

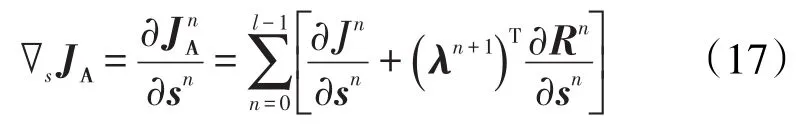
根据式（15）和式（16）便可对λ进行求解，计算得到相应的λ后，便可求得各时间步目标函数的增广Lagrange函数关于控制变量的梯度，即当s接近最优解时=0，即式（14）的右边5项都为0，满足一阶变分条件，目标函数能取得极大值。由式（17）可得目标函数的增广Lagrange函数关于控制变量的梯度为

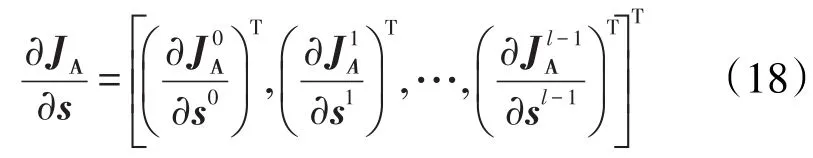
将式（18）代入式（12）可构建二次规划子问题。

2.3 Hessen矩阵的更新

在构建二次规划子问题的过程中，增广La⁃grange函数关于控制变量的Hessen矩阵的构建尤为重要。Hessen矩阵的构建主要用到了控制变量、伴随梯度、等式约束条件及不等式约束条件等。正定拟牛顿近似可用任何拟牛顿法进行更新，其中BFGS算法更常用，其表达式为

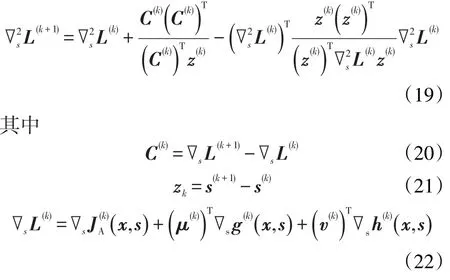
3 模型求解

利用改进的SQP算法来进行油藏生产优化的步骤为：①设定满足约束条件的初始控制变量、La⁃grange乘子及初始正定Hessen矩阵；②利用伴随法计算目标函数的梯度，采用BFGS算法更新Hessen矩阵；③构建QP子问题，求解搜索方向，并计算La⁃grange乘子；④沿搜索方向进行线性搜索得步长，更新控制变量 s(k+1)=s(k)+α(k)Δs(k+1)；⑤判断搜索方向或者目标函数，如果小于最小界限则结束，若大于最小界限，则返回步骤②重新迭代计算。

4 可行性验证

以二维三相油藏模型为例进行测试。油藏模型网格数为25×25×1，尺寸为30 m×30 m×6 m，孔隙度为0.2，渗透率及井位分布如图1所示。共有4口生产井，9口注水井；油藏原始压力为38 MPa，生产井产液量为72 m3/d，注采比为1∶1。原油价格为2 243.35元/t；产出水处理费用为672.12元/t，忽略注水成本。模拟生产时间为1 800 d，分10个时间步，即0，180，360，540，720，900，1 080，1 260，1 440和1 620 d。优化时生产制度为定液量生产，对产液量进行约束，产液量的下界为0，上界为95 m3/d；注水量下界为0，上界为48 m3/d。分别对总注入量及总产出量进行等式约束（注采比为1∶1）和不等式约束（注采比不等于1∶1），上限设为250 m3/d。

图1 油藏原始渗透率及井位分布

由优化后360，1 080，1 800 d时的驱替效果对比（图2）可知，等式及不等式约束的优化方案都抑制了水驱的指进现象，采出程度都较初始方案有了明显的改善。总注入量不等式约束下的优化调控过程与等式约束下的优化调控过程类似，在180 d后，高渗流通道中的Pro4井一直处于关井状态，阻止由Inj8井和Inj6井联合注水所导致的注入水沿高渗透层位突破；同时Pro1井调控至最大产液量，为避免注入水突破至Pro1井井底，与Pro1井处于同一高渗透条带的Inj2井一直处于关井状态。

图2 优化前后驱替效果

由优化前后开发指标对比（表1）及累积产油量与含水率的关系（图3）可看出，总注入量等式约束条件下的最优开发方案，累积产油量增加12.8%，累积注水量下降11.1%，累积产水量下降22.3%，含水率下降4.16%；总注入量不等式约束下的最优开发方案，累积产油量增加29.1%，累积注水量下降26.9%，累积产水量下降30.3%，含水率下降了4.16%。由经济净现值对比可知，不等式约束的开发方案优化效果要好于等式约束的优化效果。但比较油藏压力发现，不等式约束条件下的油藏压力损失严重，开发过程中井底流压下降到泡点压力，会改变液流相态，这对油藏开发非常不利。因此，实际应用时应添加约束下限，在维持一定地层压力的条件下获得相对较优的开发方案。

表1 开发指标对比

图3 优化前后累积产油量与含水率的关系

5 实例应用

运用该方法对胜利油区埕岛油田27A区块进行开发方案调整优化。该井区共完钻井5口，油井开井2口（27A-1和27A-5井），注水井开井2口（27A-4和27A-6井），27A-3井已关停，主力生产层位为Ng35，Ng36和Ng45。投产始于1998年2月，2002年3月开始转注，井区按驱动能量可划分为天然能量开发阶段和注水开发阶段。截至2012年3月，该区块的采出程度为14.95%。利用数值模拟方法预测5 a生产指标，期间累积产油量为4.96×104t，采出程度为18.35%。

利用动态配产配注方法，对注入量采用等式约束优化，保持总注入量不变；油井设定最小流压下限，水井保持总注入量不变。27A-1和27A-5井井底流压初始值为6 MPa，上、下边界分别为7和5 MPa。开发过程中约束27A-4和27A-6井的总注入量为240 m3/d，注入量上界和下边界分别为240和0 m3/d。原油的价格为2 170元/t，处理产出水的费用为10元/t，注水成本为5元/t，折算率为0.1。同样预测5 a，每半年调控1次，优化时间步为10（0，182，365，547，730，912，1 095，1 277，1 460和1 642 d）。

由优化前后的累积产油量、累积产水量和含水率对比（图4）可知，优化后含水率无明显增长，累积产油量的增幅超过了累积产水量的增幅，达到了增油控水的目的。在注水总量保持不变的前提下，增油效果得益于27A-4井注入量的增加，而相应27A-6井的注入量减少，使得27A-4井周围的波及系数增大，减小了27A-6井注入水的指进，优化后的剩余油明显少于优化前（图5）。优化后的采出程度达19.27%，相对于优化前增长了0.92%，累积增油量为1.13×104t，净现值增长了35%。

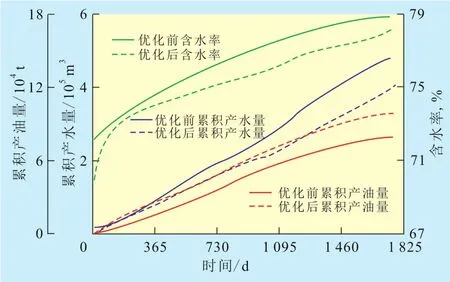
图4 优化前后累积产油量、累积产水量和含水率对比

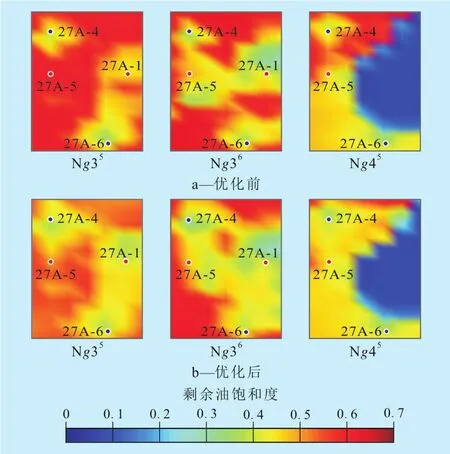
图5 埕岛油田27A区块各小层优化前后剩余油饱和度对比

6 结论

提出了一种新的油藏动态生产优化方法。该方法引用伴随方法求解得到的控制变量关于增广Lagrange函数的梯度值，采用BFGS方法更新Hessen矩阵，以此构建QP优化问题，通过求解一系列的QP问题，最终得到生产优化的最优方案。

改进的SQP生产优化方法结合了伴随方法求解梯度快速有效及SQP快速全局收敛的优点。实例测试表明，该方法是一种灵活高效的生产优化方法。改进的SQP算法在生产优化中，总注入量及采出量不等式约束下的优化效果好于等式约束条件下的优化效果，但后者油藏压力损失严重，对油藏开发非常不利。为了得到合理的开发方案，需要对总注入量及采出量进行等式约束或者在不等式约束的基础上添加约束下限。

［1］ 郝雪峰，尹丽娟.油藏类型与属性的动力学涵义［J］.油气地质与采收率，2013，20（2）：1-4.

［2］ 郑爱玲，王新海.复杂断块油藏高含水期剩余油精细挖潜方法［J］.石油钻探技术，2013，41（2）：99-104.

［3］ 郭元岭.油气勘探发展基本规律［J］.石油实验地质，2013，35 （1）：72-75.

［4］ 陈月明.油藏经营管理［M］.东营：中国石油大学出版社，2007.

［5］ 赵兰水，罗东坤.最优化理论与方法在油田产量优化研究中的改进［J］.技术经济，2006，25（10）：44-47.

［6］ 马立平，任宝生，刘志斌.最优化方法及其在油田开发规划中应用综述［J］.石油规划设计，2009，20（5）：10-14.

［7］ 任闽燕，姜汉桥.非常规天然气增产改造技术研究进展及其发展方向［J］.油气地质与采收率，2013，20（2）：103-107.

［8］ Goldberg D E.Genetic algorithms in search，optimization，and ma⁃chine learning［M］.New York：Addison-Wesley，1989.

［9］ Press W H，Flannery B P.Numerical recipes in C：The art of scien⁃tific computing［M］.Cambridge：Cambridge University Press，1992.

［10］Gill P E，Murray W.Practical optimization［M］.New York：Aca⁃demic Press，1982.

［11］Fathi Z，Ramirez W F.Optimization of an enhanced oil recovery process with boundary controls—a large-scale non-linear maximi⁃ zation［J］.Automatica，1987，23（3）：301-310.

［12］Mehos G J，Ramirez W F.Use of optimal control theory to optimize carbon dioxide miscible-flooding enhanced oil recovery［J］.Jour⁃nal of Petroleum Science and Engineering，1989，2（4）：247-260.

［13］Liu W，Fred Ramirez W.Optimal control of three-dimensional steam flooding processes［J］.Journal of Petroleum Science and En⁃gineering，1994，11（2）：137-154.

［14］宋杨.薄层稠油水平井蒸汽驱优化设计［J］.断块油气田，2013，20（2）：239-245.

［15］Zakirov I S，Aanonsen S I.Optimization of reservoir performance by automatic allocation of well rates［C］.5th European Conference on the Mathematics of Oil Recovery，1996.

［16］Asheim H.Maximization of water sweep efficiency by controlling production and injection rates［C］.European Petroleum Confer⁃ence，1988.

［17］Virnovsky G A.Water flooding strategy design using optimal con⁃trol theory［C］.6th European Symposium on Improved Oil Recov⁃ery，1991.

［18］Sudaryanto B，Yortsos Y C.Optimization of displacements in po⁃rous media using rate control［C］.SPE 71509，2001.

［19］Brouwer D R，Jansen J D.Dynamic optimization of water flooding with smart wells using optimal control theory［C］.European Petro⁃leum Conference，2002.

［20］Bieker H，Slupphaug O，Johansen T.Real-time production optimi⁃zation of oil and gas production systems：A technology survey［J］. SPE Production&Operations，2007，22（4）：382-391.

［21］Sarma P，Aziz K，Durlofsky L J.Implementation of adjoint solution for optimal control of smart wells［C］.SPE Reservoir Simulation Symposium，2005.

［22］Lien M，Brouwer D，Mannseth T，et al.Multiscale regularization of flooding optimization for smart field management［J］.SPE Journal，2008，13（2）：195-204.

［23］何立华，李博然.油气配产问题的多目标规划模型及实证研究［J］.价值工程，2010，29（23）：100-102.

［24］Wang C，Li G，Reynolds A.Production optimization in closedloop reservoir management［J］.SPE Journal，2009，14（3）：506-523.

［25］Alhuthali A H，Datta-Gupta A，Yuen B，et al.Optimal rate control under geologic uncertainty［C］.SPE 113628，2008.

［26］李斌，张国旗.年度措施产油量配产方法研究［J］.石油学报，2001，22（2）：70-78.

［27］冯其红，石飞.提液井合理井底流动压力的确定［J］.油气地质与采收率，2011，18（2）：74-76.

［28］唐焕文，秦学志.实用最优化方法［M］.大连：大连理工大学出版社，2004.

编辑武云云

TE34

：A

：1009-9603（2014）01-0045-06

2013-11-18。

张凯，男，副教授，博士，从事油气渗流、自动历史拟合及生产优化方面的教学及研究工作。联系电话：15865579293，E-mail：reservoirs@163.com。

国家重大专项“海上大井距多层合采稠油油藏开发生产实时优化技术研究”（2011ZX05024-002-008）,国家自然科学基金“油藏生产动态实时优化方法研究”（61004095），高等学校博士学科点专项基金“油田水驱体系最优调控理论方法研究”（20100133120003），中央高校基本科研业务费专项资金资助“自适应井网优化理论与方法研究”（13CX02053A），长江学者和创新团队“复杂油藏开发和提高采收率的理论与技术”(IRT1294)。