高强混凝土剪力墙屈服位移计算方法
2014-03-06赵花静梁兴文
赵花静,梁兴文,宋 璨
(西安建筑科技大学a.理学院;b.土木工程学院,西安 710055)
高强混凝土剪力墙屈服位移计算方法
赵花静,梁兴文,宋 璨
(西安建筑科技大学a.理学院;b.土木工程学院,西安 710055)
考虑高强混凝土受压强度高等特点,在高强混凝土剪力墙截面刚达到屈服状态时,假定截面受压区混凝土压应力为线性分布,基于平截面假定,用弯矩 曲率分析法得到了剪力墙截面屈服曲率公式。采用屈服曲率公式,对影响高强混凝土剪力墙屈服曲率的参数进行了分析。结果表明,除轴压比外,纵向受力钢筋屈服应变对屈服曲率影响最大;在轴压比较大时,剪力墙截面两端翼墙的影响也较大。通过对计算结果的回归分析,提出了考虑轴压比、纵向受力钢筋屈服应变和剪力墙截面两端翼墙面积影响的屈服曲率计算公式。提出了高强混凝土剪力墙顶点屈服位移的计算公式,公式的计算值与12个高强混凝土高悬臂墙顶点屈服位移的试验值比较吻合。简化公式也适用于普通混凝土剪力墙的屈服位移计算。
高强混凝土;剪力墙;屈服曲率;屈服位移;抗震性能设计
20世纪90年代以来,建筑结构基于变形/位移的抗震设计受到地震工程界的广泛关注,并提出了一些具体的设计理论和方法[1-9]。其中有些方法在设计开始即以结构变形(侧移等)作为设计变量,选取性能准则,确定满足性能准则的基底剪力需求,然后对结构进行刚度和承载力设计,并对构件截面进行变形能力设计。Tjhin等[8]采用剪力墙顶点屈服侧移和墙基础处的塑性转角作为设计变量,对剪力墙结构进行设计。结果表明,剪力墙顶点屈服侧移和墙基础处的塑性转角均有可能控制设计,取决于所采用的性能目标。
用基于位移的抗震设计方法对剪力墙结构进行设计时,其屈服位移是一个重要参数。Wallace等[1]认为普通混凝土剪力墙的屈服曲率范围在0.002 5/hw和0.003 5/hw之间或以上,其中hw是剪力墙截面高度。Priestley等[2]为了简化计算,提出的剪力墙截面屈服曲率计算公式仅与纵向受力钢筋的屈服应变和截面高度有关。钱稼茹等[3]基于平截面假定给出了混凝土剪力墙截面屈服曲率的计算公式,并根据试验结果,提出了剪力墙截面屈服时受压边缘混凝土应变的计算公式。Tjhin等[5]采用弯矩 曲率分析法,给出了延性混凝土剪力墙屈服位移的计算公式,其屈服位移公式仅与轴压比和纵向受力钢筋的屈服应变有关。上述关于混凝土剪力墙屈服曲率或屈服位移的计算方法或公式,基本上是以普通混凝土剪力墙为研究对象而提出的,由于高强混凝土的脆性以及一些基本性能参数与普通混凝土有一定差异,因此本文以高强混凝土剪力墙作为研究对象提出其顶点屈服位移的计算公式。
高强混凝土具有高强度、高耐久性、高流动性及高抗渗性能等优点,在高层及超高层建筑的底部若干层采用高强混凝土剪力墙抵抗水平荷载,可以减小剪力墙厚度,提高房屋的使用面积,具有明显的经济效益和社会效益。因此,研究高强混凝土剪力墙屈服位移的计算方法,将为这种剪力墙结构基于位移的抗震设计提供依据。
考虑高强混凝土受压强度高等特点,假定截面屈服时受压区混凝土压应力为线性分布,基于平截面假定,用弯矩 曲率分析法得到了剪力墙截面屈服曲率公式。采用参数分析法,对影响高强混凝土剪力墙屈服曲率的参数进行了分析,提出了考虑轴压比、纵向受力钢筋屈服应变和剪力墙截面两端翼墙面积影响的屈服曲率简化计算公式以及相应的剪力墙顶点屈服位移计算公式。
1 剪力墙截面屈服曲率计算
1.1 骨架曲线
根据剪力墙试件在低周反复水平荷载作用下的滞回曲线,取其外包线得骨架曲线,并将其简化为4线型,如 图 1 所 示。图 中 Mcr、φcr、My、φy、Mp、φp、Mu、φu分别表示开裂点、屈服点、峰值点和极限点对应的弯矩和曲率。
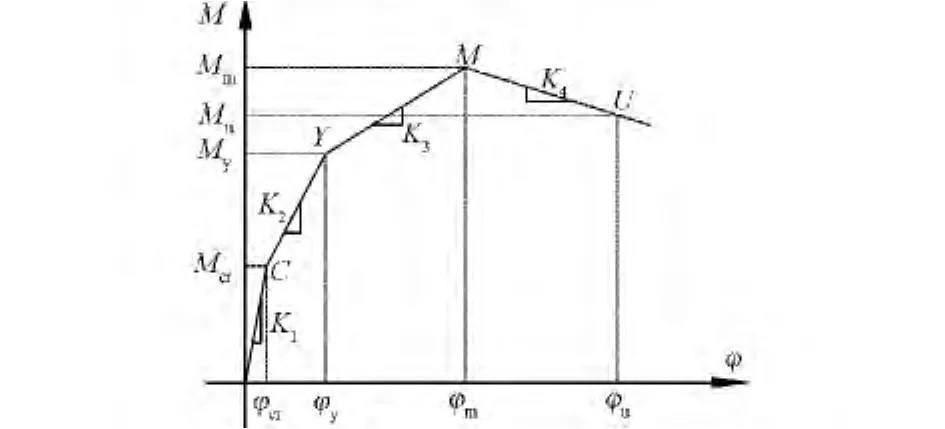
图1 弯矩 曲率骨架曲线
1.2 剪力墙截面屈服时的应力、应变分布
对于高悬臂混凝土剪力墙,以弯曲变形为主,故假定截面在变形后保持平面。当混凝土剪力墙截面受拉区纵向受力钢筋应变达到钢筋屈服应变εy时,剪力墙截面达到屈服极限状态,相应的受压区边缘混凝土应变为εc,如图2(a)所示。分析时不考虑受拉混凝土的作用;由于高强混凝土的受压强度很高,故假定受压区混凝土应力仍为线性分布,如图2(b)所示。在平截面假定的前提下,对称配筋矩形截面剪力墙在屈服状态下的截面竖向分布钢筋的应力分布如图2(c)所示。

图2 剪力墙截面屈服状态应力、应变图
1.3 平衡方程
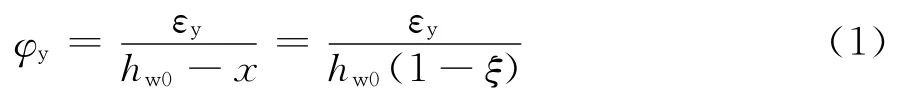
由图2(a)所示的剪力墙截面应变分布,可得截面的屈服曲率φy为式中:εy为钢筋的屈服应变;hw0为剪力墙截面有效高度;ξ为剪力墙截面受压区相对计算高度。
屈服曲率φy可采用弯矩 曲率分析来确定,应满足应变协调、材料应力 应变关系和平衡条件。
根据图2所示的截面竖向力的平衡条件,可得

式中:bw为剪力墙截面厚度;hw、hw0分别为剪力墙的截面高度、有效高度;ρs、ρ′s分别为截面端部受拉、受压纵筋的配筋率;ρw为腹板竖向分布钢筋配筋率;fc为混凝土轴心抗压强度;fy为受拉钢筋的屈服强度;Es、Ec分别为钢筋和混凝土的弹性模量;λn为轴压比;a′s为受压钢筋合力点至截面受压区边缘的距离;As、A′s分别为受拉和受压区纵向钢筋的截面面积。
联立公式(1)与(2),可求得截面相对受压区高度ξ和屈服曲率φy。
1.4 影响因素分析
由式(2)可见,影响混凝土剪力墙截面屈服曲率的因素有:截面尺寸bw和hw、截面受压区相对高度ξ、截面端部受拉、受压钢筋的配筋率ρs、ρ′s、腹板竖向分布钢筋配筋率ρw、混凝土轴心抗压强度fc、钢筋屈服强度fy和轴压比λn等。为了分析各因素对截面屈服曲率的影响程度,表1列出了各因素的变化范围及取值;对于I形截面剪力墙,还考虑了翼墙尺寸的影响。

表1 参数及取值
对表1所列的5个参数(有翼墙时为6个参数),每次考察其中一个参数,其他参数取固定值(取其常用值),对所考察的参数,分别按表1取值,计算其屈服曲率,并绘出屈服曲率与相应参数的关系曲线,考察其变化规律及相关性。分析步骤如下:
1)选定截面尺寸、材料强度,确定所考察的参数及其他参数,联立求解方程(1)与(2),得到屈服曲率。
2)变化所选定的参数,重复第(1)步,得到相应的屈服曲率。
3)绘出屈服曲率与相应参数的关系曲线。
4)评价其相关性。
按上述方法,共进行了40组(有翼墙时为160组)分析,绘制了40组(有翼墙时为160组)屈服曲率与相应参数的关系曲线,各组曲线规律基本相同。图3为其中的一组,绘制这组曲线所采用的参数为:截面尺寸为250 mm×6 000 mm,端部纵筋配筋率取0.5%,腹板竖向分布钢筋配筋率取0.30%,混凝土强度等级取C60,端部受力钢筋取HRB400,竖向分布钢筋取HRB335,混凝土和钢筋强度分别取其平均值,轴压比取0.20,工字型截面端部纵筋配筋率取2%,翼墙长宽比取5.0。
图3中的每个图均以轴压比λn为横坐标,以屈服曲率系数kφ(屈服曲率与截面有效高度hw0之乘积)为纵坐标,绘制当端部纵筋配筋率ρs、腹板竖向分布钢筋配筋率ρw、混凝土强度fc以及钢筋屈服强度fy分别取不同值时与曲率的关系图。
从图3可以看出,对于所考虑参数的取值范围,矩型截面和I型截面的屈服曲率与相应参数的关系曲线都表现出相同的规律。由图3(a)、(b)可见,腹板竖向分布钢筋配筋率对矩形截面屈服曲率几乎没有影响,对工字型截面,当轴压比较大时,腹板竖向分布钢筋配筋率对屈服曲率影响越来越小。由图3(c)、(d)可见,轴压比较大时,混凝土强度对屈服曲率产生一定影响,但在轴压比为0.3时,影响程度只有8.6%((4.4-4.05)/4.05=8.6%)。由图3(e)、(f)可见,端部纵筋配筋率随着轴压比的增大,其影响程度越来越小,当轴压比为0.3时,影响程度只有7%。由图3(g)、(h)、(i)可见,钢筋强度等级对屈服曲率影响最大,剪力墙两端的翼墙尺寸对屈服曲率的影响较大。

图3 不同参数时屈服曲率系数
1.4 剪力墙截面屈服曲率的简化计算公式
由上述分析可见,对屈服曲率影响较大的因素除轴压比外,还有纵向受力钢筋的应变和剪力墙两端翼墙面积。另外,由图3可见,屈服曲率与轴压比、纵向受力钢筋的应变和剪力墙两端翼墙面积均近似呈线性关系,故可用线性函数关系进行分析。
经过多元线性回归分析,得出屈服曲率的方程为
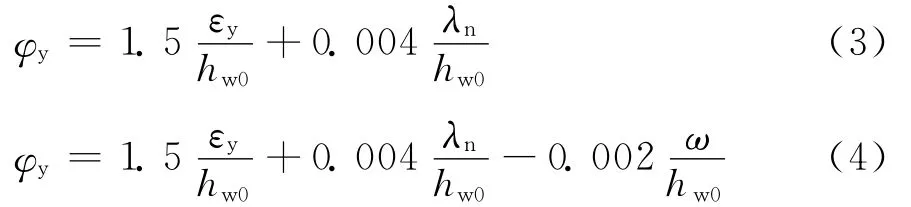
式(3)适用于矩形截面剪力墙;式(4)适用于工字型截面剪力墙,其中ω表示剪力墙截面一端两侧翼墙面积之和与全截面面积之比值。
2 屈服位移计算
定义剪力墙基础顶面截面弯曲屈服时相应的位移为屈服位移,且仅考虑截面弯曲变形的影响。当假定剪力墙的质量和刚度沿高度分布均匀时,对作用顶点集中荷载、均布荷载和倒三角形分布荷载的剪力墙,其顶点屈服位移分别为

式中,αΔ为剪力墙顶点屈服位移系数,其值主要取决于荷载形式。
实际工程中的剪力墙比较复杂,其质量和刚度沿高度有变化,各质点处的水平地震作用一般与其质量和侧移值有关,顶点屈服位移亦如此。因此,确定剪力墙顶点屈服位移系数αΔ时,可采用第一振型的振型值与质量乘积成比例的侧向力分布,并考虑剪力墙截面开裂对其刚度的影响,按弹性分析方法计算,其结果见表2,其中n表示剪力墙结构的总层数。
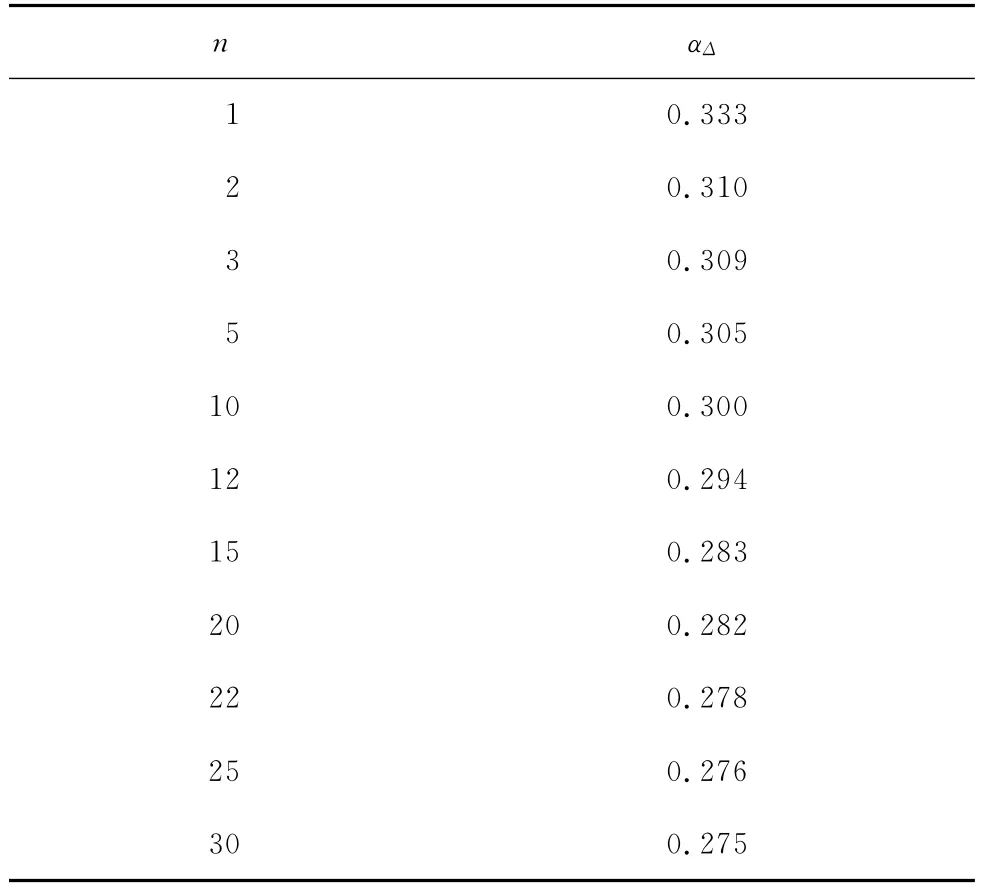
表2 剪力墙顶点屈服位移系数αΔ
3 试验验证
3.1 试验数据
试验数据取自文献[11~14],实测混凝土立方体抗压强度在72.97~93.85 N/mm2之间,计算时混凝土强度取其轴心抗压强度平均值,钢筋强度取屈服强度平均值。12个悬臂高强混凝土剪力墙试件参数如表3所示,其中HPCW-1~HPCW-4为矩形截面高性能混凝土剪力墙,SHSCW-1~SHPCW-8均为矩形截面的型钢高强混凝土剪力墙。所有试件均在剪力墙顶点作用水平集中荷载,且均发生弯曲破坏。

表3 试件参数
3.2 屈服位移计算值与试验值的比较
按式(3)计算剪力墙基础顶面截面的屈服曲率,按式(7)计算剪力墙顶点屈服位移,其中屈服位移系数αΔ取1/3,同时考虑剪力墙开裂后刚度的退化,其计算结果如表4所示。从表4可见,按本文公式计算所得的屈服位移值与试验值相比,误差在10%以内,吻合较好。
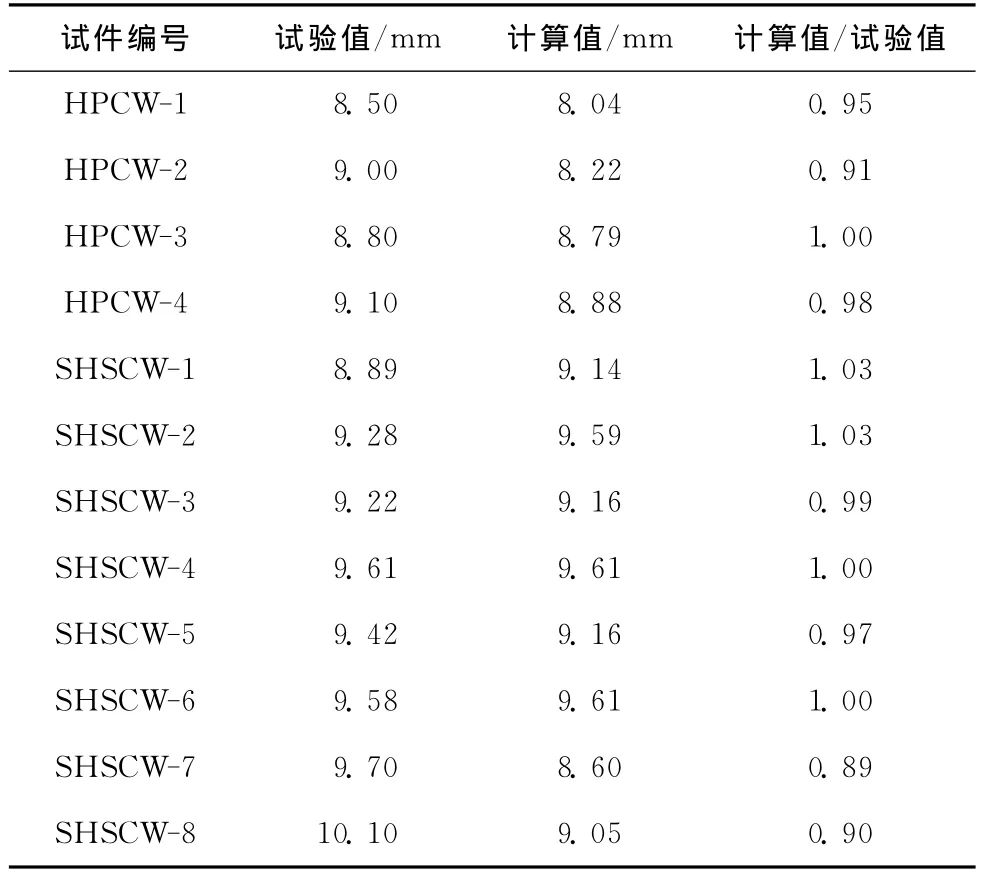
表4 屈服位移计算值与试验值的比较
4 结 论
1)弯矩 曲率分析结果表明,影响高强混凝土剪力墙屈服曲率的因素有:截面端部受拉、受压钢筋的配筋率、腹板竖向分布钢筋配筋率、混凝土轴心抗压强度、钢筋屈服强度和轴压比。在这些因素中,对剪力墙截面屈服曲率影响最大的因素为纵向受力钢筋的屈服应变,其次为轴压比;在轴压比较大时,剪力墙截面两端的翼墙也有一定影响。
2)本文提出的高强混凝土剪力墙截面屈服曲率计算公式,考虑了轴压比、纵向受力钢筋屈服应变和剪力墙截面两端翼墙的影响。基于该屈服曲率公式,所得的剪力墙顶点屈服位移计算公式,其计算值与12个高悬臂高强混凝土剪力墙屈服位移试验值比较吻合。因混凝土对其影响不大,该屈服位移计算公式也适用于普通混凝土剪力墙的屈服位移计算。
[1]Wallace J W,Moehle J P.Ductility and detailing requirements of bearing wall buildings[J].Journal of Structural Engineering,1992,118(6):1625-1644
[2]Priestley M J N.Aspect of drift and ductility capacity of rectangular cantilever structural walls[J].Bulletin of New Zealand Society for Earthquake Engineering,1998,31(2):73-85.
[3]钱稼茹,吕文,方鄂华.基于位移延性的剪力墙抗震设计[J].建筑结构学报,1999,20(3):42-49.
Qian J R,Lyu W,Fang E H.Displacement ductilitybased aseismic design for shear walls[J].Journal of Building Structures,1999,20(3):42-49.
[4]Thomsen J H,Wallace J.Displacement-based design of slender reinforced concrete walls-experimental verification [J].Journal of Structural Engineering,2004,130(4):618-630.
[5]Tjen N T,Mark A A,John W W.Yield displacement estimates for displacement-based seismic design of ductile reinforced concrete structural wall buildings [C]//13thWorld Conference on Earthquake Engineering,Vancouver B C,Canada 2004.
[6]梁兴文,黄雅捷,杨其伟.钢筋混凝土框架结构基于位移的抗震设计方法研究[J].土木工程学报,2005,38(9):53-60.
Liang X W,Huang Y J,Yang Q W.Displacementbased seismic design method of RC frames[J].China Civil Engineering Journal,2005,38(9):53-60.
[7]钱稼茹,徐福江.钢筋混凝土剪力墙基于位移的变形能力设计方法[J].清华大学学报:自然科学版,2007,47(3):305-308.
Qian J R,Xu F J.Displacement-based deformation capacity design method of RC cantilever walls[J].Journal of Tsinghua University:Science and Technology,2007,47(3):305-308.
[8]Tjen N,Tjhin M A,Aschheim J W W.Yield displacement-based seismic design of RC wall buildings[J].Engineering Structures,2007,29:2946-2959.
[9]梁兴文,赵花静,邓明科.考虑边缘约束构件影响的高强混凝土剪力墙弯矩 曲率骨架曲线参数研究[J].建筑结构学报,2009(Sup 2):62-67.
Liang X W,Zhao H J,Deng M K.Moment–curvature relationship analysis of high-strength concrete shear wall with partially confined end-zones [J].Journal of Building Structures,2009(Sup 2):62-67.
[10]应勇.钢筋混凝土剪力墙构件屈服位移研究[J].低温建筑技术,2010,12:38-40.
Ying Y.Study on yield displacement for reinforced concrete shear walls [J]. Low Temperature Architecture Technology,2010,12:38-40.
[11]梁兴文,邓明科,张兴虎,等.高性能混凝土剪力墙性能设计理论的试验研究[J].建筑结构学报,2007,28(5):80-88.
Liang X W,Deng M K,Zhang X H,et al.Experimental study on performance-based seismic design of high performance concrete shear wall [J].Journal of Structural Engineering,2007,28(5):80-88.
[12]梁兴文,辛力,邓明科,等.高性能混凝土剪力墙抗震性能及其性能指标试验研究[J].土木工程学报,2010,43(11):55-59.
Liang X W,Xin L,Deng M K,et al.Experimental study on seismic behavior and performance indexes of high-strength concrete shear walls [J].China Civil Engineering Journal,2010,43(11).
[13]梁兴文,杨鹏辉,崔晓玲,等.带端柱高强混凝土剪力墙抗震性能试验研究[J].建筑结构学报,2010,31(1):23-32.
Liang X W,Yang P H,Cui X L,et al.Experimental study on seismic behavior of high performance concrete shear wall with boundary columns [J].Journal of Building Structures,2010,31(1):23-32.
[14]梁兴文,马恺泽,李菲菲,等.型钢高强混凝土剪力墙抗震性能试验研究[J].建筑结构学报,2011,32(6):68-75.
Liang X W,Ma K Z,Li F F,et al.Experimental study on seismic behavior of SHSC structural walls [J].Journal of Building Structures,2011,32(6):68-75.
[15]梁兴文,寇佳亮,邓明科.高强混凝土剪力墙性能指标研究[J].建筑结构,2012,42(4):90-93.
Liang X W,Kou J L,Deng M K.Reseach on performance index of high-strength concrete shear walls[J].Building Structure,2012,42(4):90-93.
(编辑 胡 玲)
Yield Displacement Calculation Method of High-Strength Concrete Shear Wall
Zhao Huajing,Liang Xingwen,Song Can
(a.College of Science;b.School of Civil Engineering,Xi'an University of Architecture and Technology,Xi'an 710055,P.R.China)
It is assumed that concrete compressive stress of the cross-section compression zone is linear distribution when the cross-section of high-strength concrete shear wall reaches yield situation.Based on the plane section assumption,the yield curvature formula of shear wall section is obtained by using moment-curvature analysis method.The parameters affecting yield curvature of high-strength concrete shear wall are studied by using the yield curvature formula.The results show that longitudinal reinforcement yield strain is the most vital factor of the yield curvature in addition to axial load ratio.When axial load ratio is larger,both wing walls of shear wall section have larger impact.The yield curvature formula is presented,considering the impact of axial load ratio,boundary reinforcement yield stress and both ends of wing walls of shear wall section based on the regression analysis of calculation results.On this basis,the vertex yield displacement formula of high-strength concrete shear wall is proposed,and the calculation results of formula correspond well to the vertex yield displacement experimental values of the 12 high-strength concrete cantilever wall.The formula is also suited for the vertex yield displacement of comment concrete shear wall.
high-strength concrete;shear wall;yield curvature;yield displacement;performance-based seismic design
TU 356.1
A
1674-4764(2014)03-0080-06
10.11835/j.issn.1674-4764.2014.03.013
2013-12-17
国家自然科学基金(81278402、51078305、50908187);长江学者和创新团队发展计划(PCSIRT)。
赵花静(1985-),女,主要从事高层建筑结构及其抗震性能设计理论研究,(E-mail)zhaohj0602@126.com。
