高强度Q460钢梁抗火性能研究（Ⅰ）——理论分析

王卫永，周一超，于宝林，彭 川

（1.重庆大学 土木工程学院，重庆 400045；2.密歇根州立大学 土木与环境工程系，美国 密歇根 48824；3.重庆理工大学 资产管理公司，重庆 400050）

高强度Q460钢梁抗火性能研究（Ⅰ）
——理论分析

王卫永1，周一超1，于宝林2，彭 川3

（1.重庆大学 土木工程学院，重庆 400045；2.密歇根州立大学 土木与环境工程系，美国 密歇根 48824；3.重庆理工大学 资产管理公司，重庆 400050）

为了得到高强度Q460钢梁高温下的抗火性能，采用有限差分法推导了高温下高强度Q460钢梁的截面温度计算方法并计算了温度分布，提出了钢梁各个组件温度的修正公式。基于常温下钢梁的整体稳定临界弯矩，根据Q460钢材的高温力学性能参数，分析得到了高强度Q460钢梁高温下临界弯矩和整体稳定验算参数；并利用等效刚度法考虑了温度不均匀分布的影响，研究了高强度Q460钢梁在不均匀温度下的极限承载力、临界温度和稳定系数。

不均匀温度；高强钢；抗火性能；钢梁

建筑高强度钢材具有强度高，塑性韧性好等优点，在建筑结构中得到了广泛应用。最典型的是中国国家体育中心，采用了大量的Q460钢材［1］。高强钢和普通钢类似，不耐火，在高温下容易发生破坏［2］。目前普通钢梁的抗火研究成果较多，例如：Skowronski［3］进行了火灾下钢梁变形研究；Burgess等［4］对受火状态下钢梁的受力性能进行了研究；Liu等［5］进行了一批约束钢梁的抗火性能试验，比较全面和系统地研究了其抗火性能；Real等［6］对工字型钢梁在高温下整体稳定性进行了试验和数值分析；Real等［7］还对火灾下钢梁的整体稳定进行了数值分析；Yin等［8］对工字型钢梁在温度不均匀分布下的整体稳定性进行了数值分析；Mesquita等［9］对无侧向约束H形钢梁的临界温度进行了试验研究和数值模拟；Zhang等［10］研究了局部火灾下约束钢梁的抗火性能；Wong［11］对温度梯度下钢梁受弯承载力的修正系数进行了深入研究；Dwaikat等［12］对约束钢梁的抗火性能进行了数值分析；李国强等［13］对轴向约束工字型焊接钢梁进行了抗火试验研究；李国强等［14－15］根据约束钢梁高温下大变形状态内力平衡理论，对高温下的约束钢梁进行了理论研究；丛术平等［16］对不同荷载比的两根H型钢简支梁进行了抗火性能试验研究；陆立新等［17］针对马鞍山钢铁公司开发的Q345级耐火钢进行了试验研究；李晓东等［18］对6根H型截面钢梁进行了火灾行为的试验研究；栾艳萍等［19］对几种不同边界约束条件下受火钢梁行为的进行了比较分析。

高强钢和普通钢都不耐火，但由于两类钢材高温力学性能的差异［20］，导致了二者在抗火性能方面存在很大的区别。此外，钢梁受火时由于各组件所处的位置不同，导致了温度的不均匀分布，目前还没有发现考虑温度不均匀分布后的高强度钢梁抗火性能研究报道。笔者基于高强Q460钢的高温力学性能，采用等效刚度法对不均匀温度下的高强度Q460钢梁的抗火性能进行了理论研究，另一篇文章［21］对温度计算结果和理论分析结果进行了验证，并提出了高强度钢梁抗火设计的简化方法。

1 钢材高温力学性能

高强度钢材由于化学成分与普通钢不同，导致其高温下力学性能与普通钢有较大的差别，所以《建筑钢结构防火技术规范》（CECS200：2006）［22］中给出的力学性能参数不适用于高强钢Q460，笔者采用刘兵等［23］的试验研究结果作为钢材的高温力学性能参数：

1）高强度Q460钢高温下屈服强度

式中：fy，T为温度T（℃）时高强度Q460钢的屈服强度；fy为常温下高强度Q460钢的屈服强度。

2）高强度Q460钢高温下弹性模量：

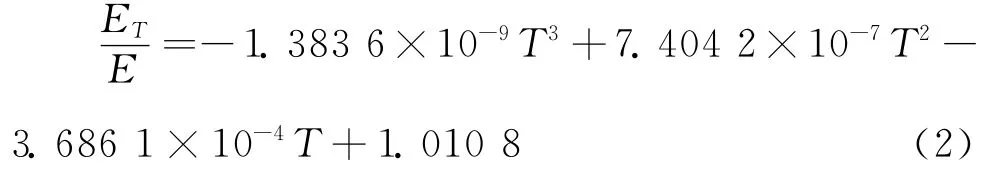
式中：ET为温度T（℃）时高强度Q460钢的弹性模量；E为常温下高强度Q460钢的弹性模量。

泊松比受温度变化影响很小，忽略高温下泊松比的变化，取值为νs＝0.3。钢材的应力 应变关系采用EC3［24］建议的公式。

2 钢梁截面温度分布

目前的抗火设计规范对单个钢构件的抗火设计没有考虑不均匀温度的问题。由于钢梁是三面受火，造成截面温度分布不均匀。三面受火的钢梁可分为3个组件：下翼缘、腹板和连接于楼板的上翼缘，根据每部分的形状系数，分别对其进行温度计算。

通过大量的热分析结果可知，在一个温度场中，钢板件温度的大小主要与构件的形状系数（单位体积的受火表面积）有关，温度的升高主要是由于热空气的热量通过对流和辐射的形式传递到板件上，而构件中板件之间的热传递较小。因此，对于单个板件（钢梁下翼缘、腹板和上翼缘），在宽度或高度范围内温度梯度不大。每一部分温度均采用板件中心的温度作为代表值进行计算和分析。

笔者进行温度分析时采用了以下基本假定：1）沿钢梁轴线方向温度保持不变；2）不考虑翼缘和腹板之间的热传导；3）忽略上翼缘和楼板之间的传热，上翼缘上表面简化为绝热状态。

火灾作用下，根据钢梁本身的截面特性，升温计算一般采用差分代替微分的方法，用增量法求得数值解。根据文献［22］，钢构件升温的计算可以采用增量法来完成，如式（3）所示，初始温度一般设定为20℃。

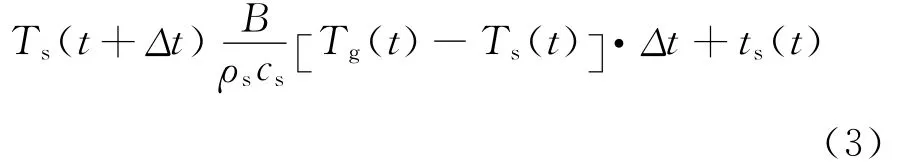
式中：Tg为钢梁周围空气的温度；Ts为钢梁的温度；Δt为时间增量，一般Δt≤30 s；cs为钢材比热容，取600 J／（kg·℃）；ρs为钢材密度；B 为钢构件单位长度综合传热系数。

采用有限差分法计算钢梁各组件的温度，下翼缘宽度、腹板高度均远大于其厚度，为节约计算机资源，取一半的模型进行计算，腹板沿厚度方向的中心线可视为绝热线。计算简图如图1（a）所示。

腹板和下翼缘的厚度设为2δ，温度的初始值设为20℃，根据热平衡原理得到腹板和下翼缘的导热微分方程和相应的初始条件、边界条件，如式（4）所示。

钢梁上翼缘可简化为单面受火，由于上部与混凝土楼板相连，采用绝热边界。计算简图如图1（b）所示。上翼缘的厚度设为2δ，根据热平衡原理可以得到上翼缘的导热微分平衡方程和定解条件，如式（6）。

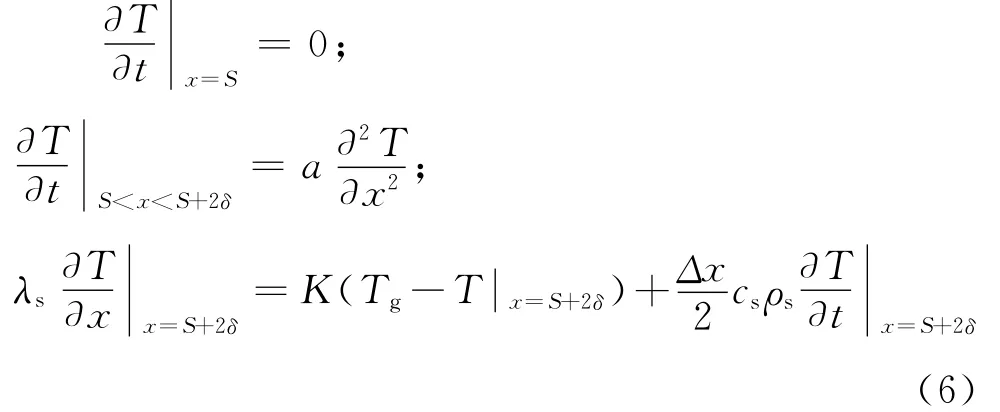
式（6）与式（4）形式相同，不同之处在于设置的绝热边界位置不同，因此式（6）转化为有限差分格式方程的过程与前述相同。

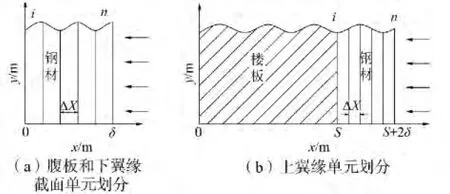
图1 有限差分法单元划分示意图

根据上面的理论和方法编制了Fortran计算机程序，给定合适的Δx和Δt，钢梁截面各部分的温度就可以求解出来，进而得到钢梁沿截面的温度分布。

采用不同尺寸的H型钢梁（截面高度250～500 mm，宽度200～300 mm，板件厚度8～15 mm），对上述两种升温计算方法增量法和有限差分法进行了对比，得到不同时刻不同位置截面的温度分布，如图2所示。从图2中可以看出，CECS200所采用的钢梁升温模型，能较好地反映均匀受火的钢梁截面的平均温度。钢梁的平均温度较接近于下翼缘的温度，腹板的温度最高，上翼缘温度最低，整个截面温度梯度较大。从图中还可以看出，当腹板和下翼缘的温度大约730℃时，温度曲线上出现短暂的平台。原因是升温模型中的材料参数采用欧规EC3［24］给定的比热容，在温度为730℃左右时，钢材的比热容达到5 000 J／（kg·K），远大于其他温度下的比热。

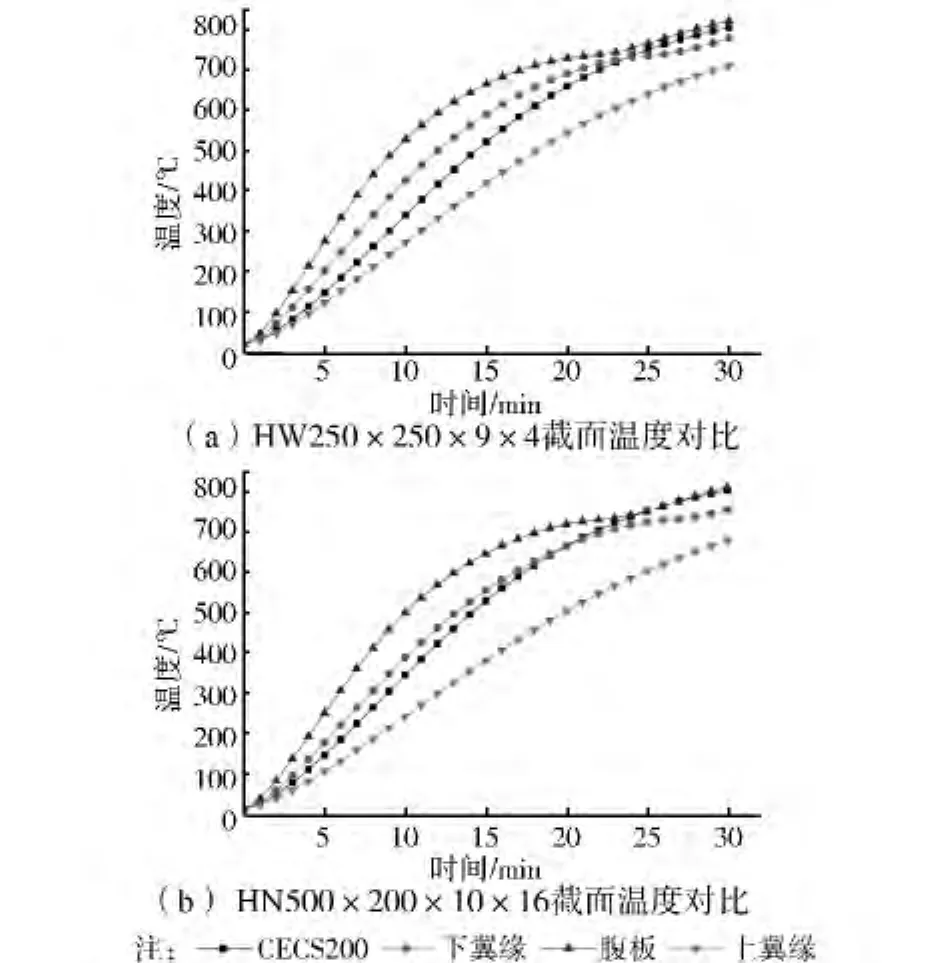
图2 CECS200和有限差分法计算结果的对比

为了方便地得到钢梁截面温度的表示方法，采取相对值的形式将各个组件的温度表示为平均温度的函数。使用线性拟合技术，得到各部件的温度修正系数。

3 钢梁的抗火性能分析

钢梁的破坏形式主要有强度破坏和整体失稳破坏两种形式，强度破坏的分析和验算可直接采用钢梁上的荷载效应与钢材的抗力的相对大小来判断。对于钢梁是否会发生侧向弯扭屈曲，主要根据钢梁发生整体失稳时的临界弯矩和所受弯矩的大小来判断。由钢梁的整体失稳理论可知，钢梁的整体稳定临界弯矩与侧向抗弯刚度、抗扭刚度、荷载分布情况及位置有关。而抗弯刚度和抗扭刚度仅与材料的弹性模量、剪切模量与截面尺寸有关。

高强度钢梁与普通钢梁相比，钢材屈服强度提高，弹性模量基本没有变化。因此，普通钢梁的稳定理论适用于高强度钢梁。此外，火灾高温对钢材的力学性能产生较大的影响，主要是降低钢材的屈服强度和弹性模量，因此，只要将常温下的弹性模量换成高温下的弹性模量，常温下的稳定理论就适用于高温下的状况。基于该分析，采用高温弹性模量代替常温弹性模量得到温度均匀分布的高强度Q460钢梁的临界弯矩。

3.1 温度均匀分布的钢梁整体稳定性能

一般情况下，钢梁的整体稳定破坏是由于承受的弯矩达到了临界弯矩。根据弹性理论，绕强轴发生弯曲的对称截面钢梁的临界弯矩计算式为

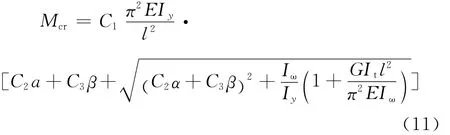
式中：C1、C2和C3为与荷载类型（均布荷载或集中荷载等）有关的系数；α为荷载作用点至截面剪力中心的距离，作用点在剪力中心上方时，取负值，反之取正值；β为截面不对称性参数，双轴对称截面为 0；Iy为钢梁截面对弱轴y轴惯性矩；Iω为钢梁截面扇性惯性矩；It为钢梁截面扭转惯性矩；l为钢梁跨度；E为钢材弹性模量；G为钢材剪切模量。

高温作用下的钢梁，只有弹性模量E和剪切模量G与温度有关，因此式（11）应当适用于高温下的情况，即

式中：McrT为高温下受弯构件临界温度；ET为温度为Ts时的弹性模量；GT为温度为Ts时的剪切模量。

根据稳定系数的含义，钢梁临界弯矩的计算公式又可写成

式中：W 为钢梁的毛截面模量；φb、φbT为弹性状态下常温和高温下钢梁的整体稳定系数。

钢梁高温和常温的整体稳定系数比值为稳定验算参数αb，不考虑温度对抗力分项系数的影响，则由式（13）可得

计算得到αb后，将常温下钢梁的整体稳定系数乘以αb即可得到高温下的整体稳定系数，当钢梁截面进入塑性状态后，需要对整体稳定系数进行塑性修正，考虑修正的高温下整体稳定系数φ′bT可采用式（16）表示，

将式（1）、式（2）代入式（15），可以得到高强Q460钢梁高温下稳定验算参数αb，并与普通钢梁的稳定验算参数进行了对比，见图3所示。再根据式（16）、式（17），即可进行高强Q460钢梁高温下的整体稳定验算。从图3中可以看出，高强钢梁与普通钢梁的稳定验算参数有很大的区别，不能使用普通钢梁的稳定验算参数进行高强钢梁的整体稳定验算。

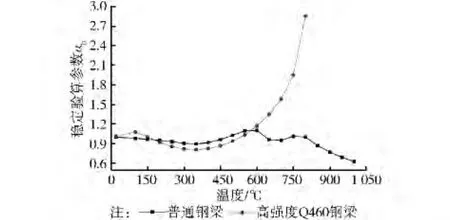
图3 普通钢梁与高强钢梁稳定验算参数的比较

3.2 温度不均匀分布的钢梁整体稳定承载力

当考虑温度不均匀分布情况时，按照式（10）对温度进行修正，并假定钢梁各个组件的温度均匀分布，可根据截面等效刚度的原则考虑温度的不均匀分布对钢梁抗弯极限承载力的影响。

假定某个时刻腹板温度为T，将T作为变量，可由式（10）计算钢梁的平均温度Ts，上下翼缘的温度分别为T1、T2。进行钢梁抗火性能分析时，钢材弹性模量根据温度和常温下的弹性模量确定。即采用式（2）的折减系数，可得到相应温度下各部分板件的弹性模量：腹板为ET，上翼缘为ET1，下翼缘为ET2。令f1（T）＝ET1／ET，f2（T）＝ET2／ET得ET1＝f1（T）ET，ET2＝f2（T）ET。

采用等效刚度法，使钢梁的两个翼缘对自身的两个对称轴抗弯刚度相同，从而对翼缘的宽度和厚度进行转换，如图4所示。

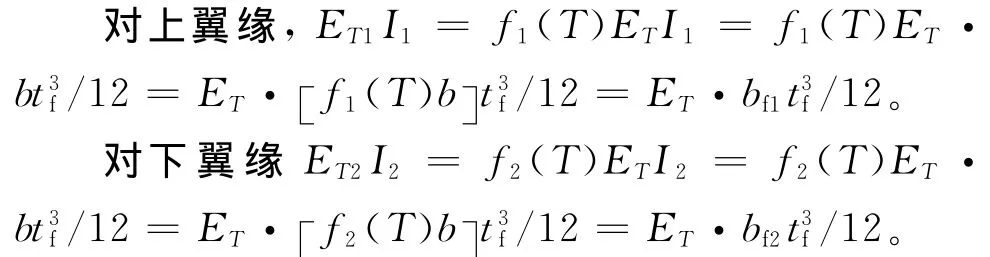
图4 考虑温度不均匀分布的截面特性参数的变化

式中：I1和I2分别为上翼缘和下翼缘对各自水平轴的惯性矩；bf1、bf2分别为等效刚度转换之后的上、下翼缘宽度。

对钢梁的板件根据弹性模量的不同进行刚度等效后，翼缘的尺寸发生了变化，截面也从双轴对称的形式变成了单轴对称，等效截面之后，截面的特性参数采用上标eq标识，将这些参数代入公式（12），即可得到温度不均匀分布的受弯构件的临界弯矩MeqcrT

式中：αeq为等效刚度后横向荷载作用点至截面剪力中心的距离；βeq为等效刚度后反映截面不对称程度的参数，按式（19）计算，

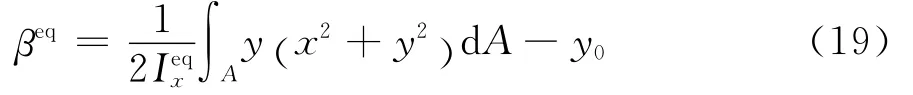
式（21）不方便应用，可按《钢结构设计规范》［25］的方法进行简化处理。把承受纯弯荷载作用时的式（21）作为代表，在一般的截面尺寸下，式（19）中的积分结果与y0相比，可以忽略，故取

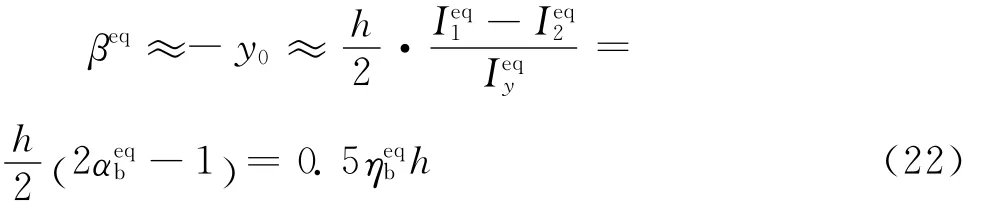
由于钢梁上翼缘连接于混凝土楼板上，其温度比腹板和下翼缘低，采用等效刚度方法后，截面变成为单轴对称截面，根据数值分析得到≈0.4，式（24）可调整为＝0.8（2－1）。

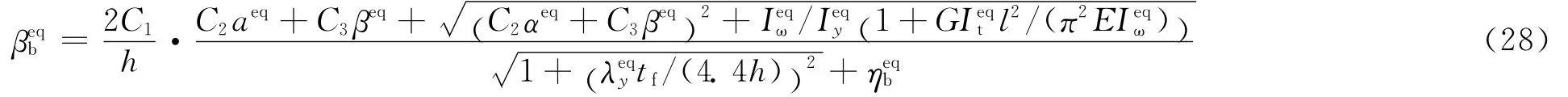
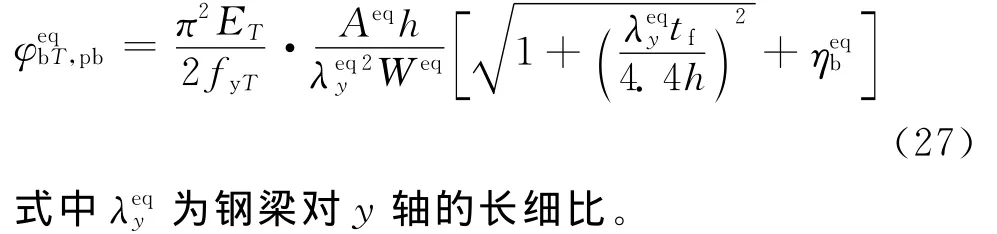
在常温下当钢梁上承受横向荷载作用时，采用等效弯矩系数βb。βb可以根据式（11）计算得到φb的数值除以纯弯作用下计算得到的φb值。文献［26］的研究表明，βb数值的分布具有一定的规律，可按照《钢结构设计规范》［25］表B.1进行计算。笔者对多个截面和多个跨度的钢梁的φb进行了计算，并将计算结果和式（11）的结果进行对比，发现吻合较好。

对温度不均匀分布的钢梁进行整体稳定性分析时，也采用上述方法。承受横向荷载作用时，高温下钢梁的整体稳定系数可采用式（21）表示，根据＝，以及λ ＝，式（21）与式（27）的比值可得y

由式（28）可知，只需将与截面有关的参数转换成等效刚度后的相应参数外，其余参数未发生变化。而且，对刚度进行等效后，截面变成了单轴对称截面，可按照《钢结构设计规范》［25］附录B.1计算相应的数值。进而，φeqbT可按照式（29）计算。

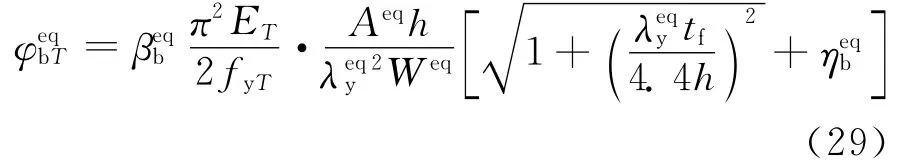
则考虑温度不均匀分布的钢梁高温下的整体稳定验算公式为

由以上分析和推导可以看出，考虑温度的不均匀分布后，分析高强度Q460钢梁的整体稳定性能时，可在普通钢梁的分析过程中，考虑高强度钢材的强度折减系数与弹性模量折减系数，即式（1）和（2），代入到式（29）中，计算得到高强度Q460钢梁温度不均分分布时的整体稳定系数，然后根据式（31）和式（32）对高强度Q460钢梁进行整体稳定校核。

3.3 临界温度

钢梁的抗弯承载力随着温度的上升而降低，当抗弯承载力和所受的弯矩相等时，此时钢梁的温度即为临界温度。荷载比指的是钢梁承担的最大弯矩和截面的抗弯承载力的比值，即

由上式可知，根据高强度Q460钢梁的整体稳定系数和荷载比，可得到其临界温度。为了便于工程应用，采用数值分析方法计算了多个荷载比和稳定系数下的临界温度数值，见图5（a）。对其他荷载比和稳定系数数值对应的临界温度，可采用插值法进行计算。

将式（33）代入式（32），由于等效刚度后截面发生改变，得到

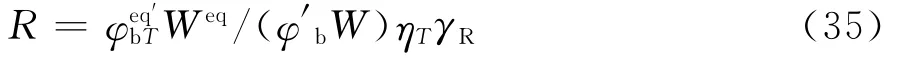
计算发现，高温下Weq／W 的比值在温度不高于780℃时，不同截面的结果差别不大，基本都在1.0～1.08之间。因此，为简化计算，忽略Weq／W 对上式计算结果的影响，可按最不利情况取值，即Weq／W ＝1.0。进而，式（35）可简化为

根据高强Q460钢梁的整体稳定系数φ′b和荷载比R，可以得到高温下承载力极限状态下考虑温度不均匀分布的高强Q460钢梁的临界温度，如图5（b）所示。

图5 高强度Q460钢梁的临界温度

4 结 论

采用有限差分法推导了高温下高强度Q460钢梁的截面温度分布，对常用钢梁的截面尺寸，即截面高度250～500 mm、宽度200～300 mm、板件厚度8～15 mm，提出了钢梁各个组件温度修正公式。根据Q460钢材的高温力学性能参数，在常温下钢梁的整体稳定临界弯矩的基础上，得到了高强度Q460钢梁的高温下临界弯矩和稳定验算参数，并利用等效刚度法考虑了温度不均匀分布的影响，推导了高强度Q460钢梁不均匀温度下的极限承载力、临界温度和整体稳定系数。

［1］王卫永，李国强，戴国欣.轴心受压高强度H型钢柱抗火性能［J］.重庆大学学报，2010，33（10）：76-82.

Wang W Y，Li G J，Dai G X.Fire-resistance performance of high-strength-steel H shaped columns under the axial compression［J］.Journal of Chongqing University，2010，33（10）：76-82.

［2］王卫永，李国强.高强度钢柱高温下承载力数值计算方法［J］.土木建筑与环境工程，2011，33（6）：13-18.

Wang W Y，Li G J.Numerical method for load bearing capacity of high strength steel columns at elevated temperature ［J］.Journal of Civil，Architectural ＆Environmental Engineering，2011，33（6）：13-18.

［3］Skowronski W.A study of the steel beam deformation during fire［J］.Building and Environment，1988，23（2）：159-167.

［4］Burgess I W，El Rimawi J，Plank R J.Studies of the behaviour of steel beams in fire ［J］.Journal of Constructional Steel Research，1991，19（4）：285-312.

［5］Liu T，Fahad M K，Davies J M.Experimental investigation of behaviour of axially restrained steel beams in fire ［J］.Journal of Constructional Steel Research，2002，58（9）：1211-1230.

［6］Real P M M Vila，Piloto P，Franssen J M.A new proposal of a simple model for the lateral-torsional buckling of unrestrained steel I-beams in case of fire：experimental and numerical validation ［J］.Journal of Constructional Steel Research，2003，59（2）：179-199.

［7］Real P M M Vila，Lopes N，Simes da Silva L，et al.Parametric analysis of the lateral-torsional buckling resistance of steel beams in case of fire［J］.Fire Safety Journal，2007，42（6／7）：416-424.

［8］Yin Y Z，Wang Y C.Numerical simulations of the effects of non-uniform temperature distributions on lateral torsional buckling resistance of steel I-beams ［J］.Journal of Constructional Steel Research，2003，59（8）：1009-1033.

［9］Mesquita L，Piloto P，Vaz M，et al.Experimental and numerical research on the critical temperature of laterally unrestrained steel I beams ［J］.Journal of Constructional Steel Research，2005，61（10）：1435-1446.

［10］Zhang C，Li G Q，Usmani A.Simulating the behavior of restrained steel beams to flame impingement from localized-fires ［J］.Journal of Constructional Steel Research，2013，83：156-165.

［11］Wong M B.Adaptation factor for moment capacity calculation of steel beams subject to temperature gradient［J］.Journal of Constructional Steel Research，2007，63（8）：1009-1015.

［12］Dwaikat M M S，Kodur V K R.A performance based methodology for fire design of restrained steel beams［J］.Journal of Constructional Steel Research，2011，67（3）：510-524.

［13］李国强.钢梁抗火计算和设计的实用方法［J］.工业建筑，1994（7）：43-46.

Li G Q.A practical approach for fire-resistant calculation and design of steel beams［J］.Industrial Construction，1994（7）：43-46.

［14］李国强，贺军利，蒋首超.约束钢梁的抗火试验与验算［J］.土木工程学报，2000，33（4）：23-26.

Li G Q，He J L，Jiang S C.Fire-resistant experiment and theoretical calculation of a restrained steel beam［J］.China Civil Engineering Journal，2000，33（4）：23-26.

［15］李国强，郭士雄.约束钢梁高温下大变形状态分析［J］.同济大学学报：自然科学版，2006，34（7）：853-858.

Li G Q，Guo S X.Analysis of restrained stell girders with large deflection subjected to elevated temperature［J］.Journal of Tongji University，2006，34（7）：853-858.

［16］丛术平，梁书亭，董毓利.简支钢梁火灾行为的试验研究［J］.东南大学学报：自然科学版，2005，35（Sup1）：66-68.

Cong S P，Liang S T，Dong Y L.Experimental investigation of behavior of simple supported steel beams under fire［J］.Journal of Southeast University：Natural Science Edition，2005，35（Sup1）：66-68.

［17］陆立新，李国强，蒋首超，等.马钢耐火钢梁的抗火试验与设计验算［J］.建筑结构，2006，36（4）：59-60，76.

Lu L X，Li G Q，Jiang S C，et al.Fire-resistant experiment and theoretical calculations of fire-resistant steel beam ［J］.Building Structures，2006，36（4）：59-60，76.

［18］李晓东，董毓利，丛术平.H型截面钢梁抗火试验研究［J］.建筑结构，2006（8）：94-96，102.

Li X D，Dong Y L，Cong S P.Anti-fire experimental research on h-section steel beams ［J］. Building Structures，2006（8）：94-96，102.

［19］栾艳萍，席丰.几种边界约束条件下受火钢梁行为的比较分析［J］.山东建筑大学学报，2012，27（5）：477-482.

Luan Y P，Xi F.Comparative analysis of different restrained beams in fire condition ［J］.Journal of Shandong Jianzhu University，2012，27（5）：477-482.

［20］Wang W Y，Liu B，Kodur V.Effect of temperature on strength and elastic modulus of high-strength steel［J］.Journal of Materials in Civil Engineering，2013，25（2）：174-182.

［21］王卫永，周一超，于宝林，等.高强度Q460钢梁抗火性能研究（Ⅱ） 理论验证［J］.土木建筑与环境工程，2014，36（1）：72-79.

Wang W Y，Zhou Y C，Yu B L，et al.Fire resistance study on high strength Q460 steel beams-Part II：Theory validation ［J］.Journal of Civil，Architectural＆ Environmental Engineering，2014，36（1）：72-79.

［22］中国工程建设标准化协会.CECS 200：2006建筑钢结构防火设计规范［S］.北京：中国计划出版社，2006.

［23］刘兵，王卫永，李国强，等.高强度Q460钢柱抗火性能研究［J］.土木工程学报，2012，45（9）：19-26.

Liu B，Wang W Y，Li G Q，et al.Study of fire resistance of high strength Q460 steel columns ［J］.China Civil Engineering Journal，2012，45（9）：19-26.

［24］European Committee for Standardization.EN 1993-1-1，Eurocode 3，Design of Steel Structures-Part 1-1 General Rules and rules for buildings［S］.2005.

［25］GB 50017－2003钢结构设计规范［S］.北京：中国计划出版社，2003.

［26］全国钢结构标准技术委员会.钢结构研究论文报告选集（第二册）［M］.北京：水利电力出版社，1982.

［27］周一超.高强度钢梁抗火性能研究［D］.重庆：重庆大学，2012.

（编辑 胡英奎）

Fire Resistance Analysis of High Strength Q460 Steel Beams-Part I：Theoretical Analysis

Wang Weiyong1，Zhou Yichao1，Yu Baolin2，Peng Chuan3
（1.College of Civil Engineering，Chongqing University，Chongqing 400045，P.R.China；2.Department of Civil and Environmental Engineering，Michigan State University，Michigan 48824，USA 3.Assets Management Company，Chongqing，Chongqing University of Technology，Chongqing 400050，P.R.China）

In order to investigate the fire resistance of high strength steel beams made from Q460，the method to compute temperature distribution of high strength Q460 steel beams was derived and the temperature distribution was calculated by using finite difference method.The modified equations of temperature for components of steel beam were proposed.According to critical moment at room temperature and mechanical properties of high strength Q460 steel at elevated temperature，the critical moment and stability checking coefficient were obtained by analysis.The load bearing capacity and critical temperature as well as stability factor were studied by using equivalent stiffness method through considering the effect of temperature gradient on stiffness.

Non-uniform temperature；high strength steel；fire resistance；steel beam

TU392

A

1674-4764（2014）03-0064-08

10.11835／j.issn.1674-4764.2014.03.011

2013-10-16

重庆市高等学校青年骨干教师资助计划；中国博士后科学基金（20110490811、2012T50765）

王卫永（1982-），男，副教授，博士，主要从事结构抗火性能研究，（Email）wywang＠cqu.edu.cn。