自耦变压器串联绕组辐向稳定性分析

白永刚，刘文里，吴明君，李 航

(1．东营供电公司，山东 东营257091;2．哈尔滨理工大学，哈尔滨150080;3．黑龙江省电力科学研究院，哈尔滨150030)

在相同容量情况下，自耦变压器比普通变压器的几何尺寸和所需要的材料都有所减少，从而降低了变压器的重量和损耗，方便了变压器的运输和安装。所以在大容量、高电压等级的情况下，自耦变压器得到了广泛的应用［1－2］。但自耦变压器比两绕组变压器的短路阻抗小，短路电流较大，由此产生的短路电动力较大，影响了绕组稳定性。对此，本文以一台500 kV/334 MVA三绕组自耦变压器为例，以磁势平衡原理为基础［3］，运用有限元软件［4］，计算出公共绕组出口处短路时，公共绕组和串联绕组的辐向短路电动力;利用瞬态分析方法，建立绕组3D模型，将前面求出的短路电动力结果加载到3D模型上，然后再求出外绕组的拉伸变形量，以此验证外绕组的稳定性。

1 自耦变压器中－高绕组运行

一台自耦变压器绕组结构如图1所示，其中1、2、3、4、5分别表示自耦变压器的低压绕组、公共绕组、串联绕组、调压绕组和激磁绕组。

在自耦变压器公共绕组和串联绕组运行时，低压绕组可以带无功补偿装置或者作为平衡绕组使用。本文讨论后一种情况，此时低压绕组不参加绕组模型建立。绕组的外电路连接如图2所示。

图2 绕组与外电路连接图Fig．2 Connection of winding and external circuit

从图2可以看到，自耦变压器公共和串联绕组之间不仅有磁的联系，而且还有电的链接。

2 计算实例

2.1 模型建立

本文计算一台500 kV/334 MVA自耦变压器绕组辐向短路电动力，变压器主要参数如表1所示。

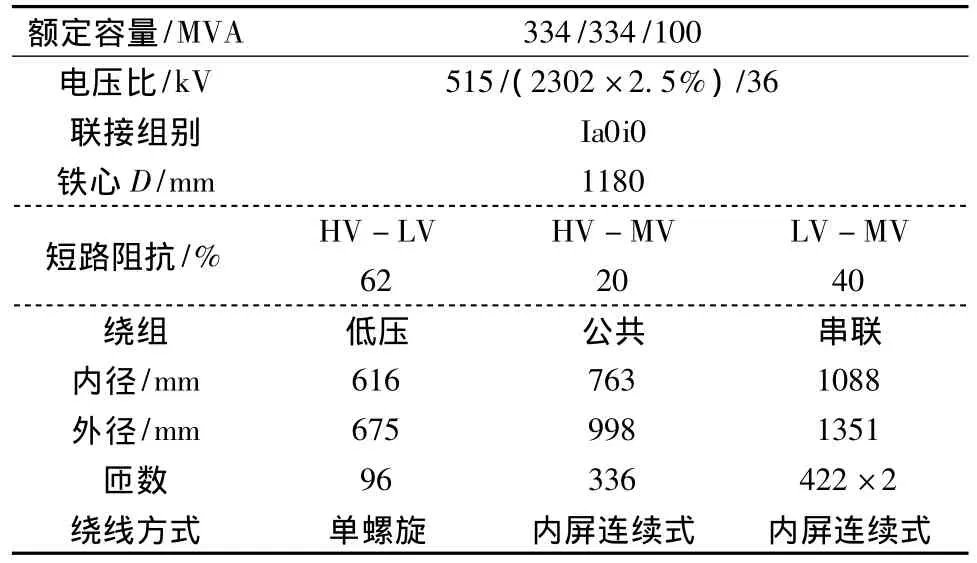
表1 变压器主要参数Tab．1 Main parameters of transformer

计算表1中所示变压器的短路电动力，利用有限元软件ANSYS，采用场－路耦合方法，即内部用场，外部采用电路耦合的方式。绕组区域以及外电路连接如图3所示，a为内部场，考虑变压器绕组结构对称性，仅建立绕组二维有限元模型，以饼为单位，每饼高度、线饼截面积、匝数以及填充系数均按实际情况考虑;b为外部电路，左侧为公共绕组，右侧为串联绕组上下两部分，导线采用阻值为电阻连接，在公共绕组和串联绕组之间加交变的相电压，采用瞬态分析方法进行求解。

2.2 计算结果

计算结果:在T=0.01 s时，绕组线饼电流密度如图4所示。

图3 绕组有限元模型与外电路连接图Fig．3 Connection of winding finite element model and external circuit

图4 绕组电流密分布Fig．4 Winding current density distribution

从图4可以看出，同一绕组不同饼间电流密值不尽相同，这是因为绕组线饼不同导线规格的缘故，此时公共绕组和串联绕组最大的短路电流值分别为13 037.56 A和－10 143.72 A，前者电流流向纸面内，后者电流流向纸面外，方向相反，满足磁势平衡关系。短路电流倍数分别为8.98和9.03。漏磁分布如图5所示，在绕组端部磁力线发生弯曲，主空道处磁力线分布最多。

T=0.01 s时，两绕组的轴向磁密如图6所示。

从图6可以看到，端部轴向磁密很小，中间线饼磁密较大，短路时刻，串联绕组中间线饼最大磁密可以达到1.29 T。

T=0.01 s时，绕组短路电动力最大，如图7、图8所示。

图5 磁力线分布Fig．5 Magnetic field lines distribution

图6 绕组轴向磁密Fig．6 Winding axial magnetic flux density

图7 T=0.01 s公共绕组辐向短路电动力Fig．7 T=0．01 s public winding radial short-circuit electrodynamic force

图8 T=0.01 s串联绕组辐向短路电动力Fig．8 T=0．01 s series winding radial short-circuit electrodynamic force

从图7、图8可以看出，公共绕组和串联绕组靠近端部部分线饼辐向短路电动力较小，公共绕组力为负值，表明短路力使绕组向内压缩;而作用于串联绕组短路力为正，使其向外拉伸。公共和串联绕组最大短路电动力发生在46线饼处和62线饼处，值分别为－48.08 kN/m和43.67 kN/m。

3 串联绕组稳定性分析

由上述分析得知，外绕组在较大的外径向力作用下，绕组会产生较大拉伸变形，且形变量的大小直接影响外绕组在短路状态下的稳定性。

3.1 拉伸变形模型的建立

绕组铜导线没有明显的屈服强度，是典型的塑性材料，绕组的应力应变关系如图9所示。

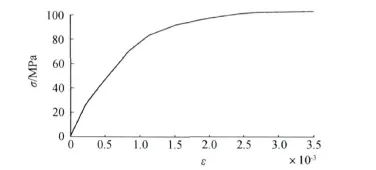
图9 绕组的应力应变关系Fig．9 Winding stress strain relation

当应力很小时，应力σ与应变ε服从虎克定律呈线性关系;当永久变形超过0.2%时，应力－应变曲线明显饱和，此时应力稍有增加，永久变形就会急剧增大，铜导线的σ0．2屈服强度为100 MPa。

串联绕组的辐向短路电动力是使绕组向外的张力，处于串联绕组与公共绕组之间的撑条对形变影响较小，故本文忽略了撑条对串联绕组产生形变的作用。

考虑绕组对称性，建立1/2串联绕组三维模型，即62饼绕组模型，线饼以梁为基础单位，输入绕组的弹性模量和泊松比，并考虑饼间油道的影响，其模型如图10所示。

图10 串联绕组62饼模型Fig．10 Series winding 62 cake model

3.2 短路动态力的加载与求解

发生短路时，由于电流和磁通是变化的，作用于某一饼的辐向短路电动力也是随时间变化的;饼与饼之间的辐向短路电动力幅值也不尽相同(由图8可知)。因此，对于如何施加短路电动力现已成为难题。

利用软件的后处理功能，提取串联绕组1～62饼在时间0～0.1 s范围内的辐向短路电动力;采用建立数组的方式存储各饼随时间变化的动态辐向短路电动力，在线饼模型建立完成之后，对应每个线饼，每隔0.0005 s施加一点力，每线饼一共200步，采用瞬态分析方法进行求解。

3.3 结果分析

在T=0.01 s时刻，绕组承受的短路电动力最大，在此短路力下，串联绕组的变形如图11所示，其上部分是绕组端部，下部分是绕组中部。

图11 T=0.01 s串联绕组形变分布图．11 T=0．01 s series winding deformation distribution

从图11中可以看到，绕组端部的变形很小，向中部移动时，绕组短路电动力逐渐增大，变形增加。在绕组的第9～17线饼处，由于导线规格不同，使得该部分，电流密度较小，导致绕组短路电动力减小，因此，造成了绕组变形较小。

由前所述，绕组第62线饼和第1线饼分别产生了最大和最小的变形量，这是因为这两线饼分别承受了最大和最小的短路电动力所致。线规不同时，绕组短路电动力变化很大。分别提取绕组第1、9、62线饼，在0.1 s时间内，绕组变形随时间变化关系，如图12所示。

由12图可以看出，绕组变形在T=0.01 s最大，其中绕组端部线饼变形量为0.32 mm，绕组最大短路电动力处线饼位移为0.47 mm，不规则线饼处位移量为0.41 mm;同时绕组变形量随时间衰减，这与绕组短路电动力大小随时间变化曲线符合，说明模拟是正确的。

3.4 位移校核

导线允许的最大位移量如式(1)所示。

图12 部分线饼变形量随时间变化曲线Fig．12 Part winding deformation curves

式中:σsav为导线辐向弯曲应力，N/mm;I0为绕组极惯性矩，mm;Fr为绕组辐向力，N;tv为单根普通导线或换位导线沿绕组辐向厚度，mm。

普通导线:

式中:wv为单根普通导线或换位导线沿绕组轴向高度，mm。

可求得串联绕组最大允许拉伸位移为2.39 mm，远大于串联绕组的最大实际位移量，由此得出，串联绕组在辐向短路电动力作用下是稳定的。

3 结论

通过上述对实例计算与分析，得出在最大短路电动力作用下，绕组中部最大位移为0.47 mm，绕组临界拉伸位移2.39 mm，临界位移大于实际最大位移。由此可知在短路电动力作用下，串联绕组是稳定的。这一结论可为技术人员今后研究自耦变压器绕组稳定性提供一定的参考。

［1］路长柏．电力变压器理论与计算［M］．沈阳:辽宁科学技术出版社，2007:280-284．LU Changbai．Power transformer theory and calculation［M］．Shenyang:Liaoning Science and Technology Press，2007:280-284．

［2］ Tang Yunqiu，Qiao Jingqiu，Xu Zihong．Numerical calculation of short－ circuitelectromagnetic forces on the transformer winding［J］．IEEETrans．Magn，1990，26(2):1039-1041．

［3］李阳阳，刘文里．三绕组变压器中压绕组短路电动力的计算方法［J］．黑龙江电力，2012，35(5):344-348．LI Yangyang，LIU Wenli．Calculation method of medium-voltage winding short circuit force of three-winding transformer［J］．Heilongjiang Electric Power，2012，35(5):344-348．

［4］阎照文．ANSYS工程电磁分析技术与实例详解［M］．北京:中国水利水电出版社，2006:429-439．YAN Zhaowen．ANSYS engineering electromagnetic analysis technique and detailed description of examples［M］．Beijing:China water Conservancy and Hydropower Press，2006:429-439．