适用于地区放射电网的无功补偿电容优化配置方法

张 旭

(东北电力大学电气工程学院，吉林吉林132012)

电网负荷包括有功和无功负荷，其中有功负荷由发电机组提供，若无功负荷也由发电机组提供，必会增加无功功率在线路中流动引起的有功损耗，甚至还可能导致负荷节点电压过低，影响供电电压质量［1－2］。所以，通常采用在各变电站配置一定的无功补偿装置实现无功功率的就地平衡，减少传输无功功率引起的有功损耗［3－4］。但无功补偿装置的增多将增大电网的投资成本，那么如何权衡无功补偿电容配置对投资成本和网损的影响，设计合理的无功补偿电容配置，提高电网运行经济性，就显现得至关重要。

曾有相关文献对无功补偿装置配置方法进行介绍，如文献［5］设计了一种基于无功裕度排序和改进遗传算法的无功补偿装置优化规划方法，可实现无功规划的可靠性和经济性;文献［6］基于无功潮流图设计了某地区电网的无功补偿装置，提高了电网运行的经济性。然而，文献［5］采用智能算法得到的优化结果并非完全意义的最优解，且算法较为繁琐复杂，不便在地区电网无功补偿电容规划中实现;文献［6］并未提出系统的无功补偿电容规划方法。由此，本文分析了地区辐射电网无功补偿容量对网损的影响机理，并在此基础上综合考虑无功补偿电容投资成本和网损，建立了无功补偿电容的优化配置方法，在满足母线电压约束条件下，权衡网损造成的经济损失，设计了地区电网的无功补偿容量，提高了电网运行经济性。

1 地区放射电网无功补偿需求分析

地区放射电网接线方式如图1所示。

地区变电站包括若干较低电压等级的变电站，本文称作子级变电站。在电网正常运行情况下地区变电站母线为平衡节点，各子级变电站母线为PQ节点或PV节点，而各子级变电站相互之间无电气连接，即在地区变电站母线电压给定情况下，单个子级变电站与地区变电站之间线路的潮流分布只与其自身负荷有关，故可将地区放射电网划分为若干只包括地区变电站和单个子级变电站的等值网络结构，等值网络结构如图2所示。

图1 地区放射电网接线方式Fig．1 Connection mode of area radiation power net

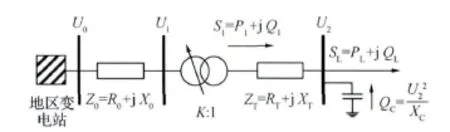
图2 两级变电站等值网络图Fig．2 Two level of substation equivalent network diagram

图2中，U0为地区变电站二次侧母线电压;Z0为连接两级变电站线路的等值阻抗;U1和U2分别为子级变电站一次侧和二次侧母线电压;ZT为子级变电站主变等值阻抗;K为变压器变比;S1为子级变电站主变一次侧功率;SL为负荷功率;XC和QC分别为电容器等值容抗和补偿容量。

当调节子级变电站主变分接头和投切电容器时，U0和SL保持不变，则有［7］:

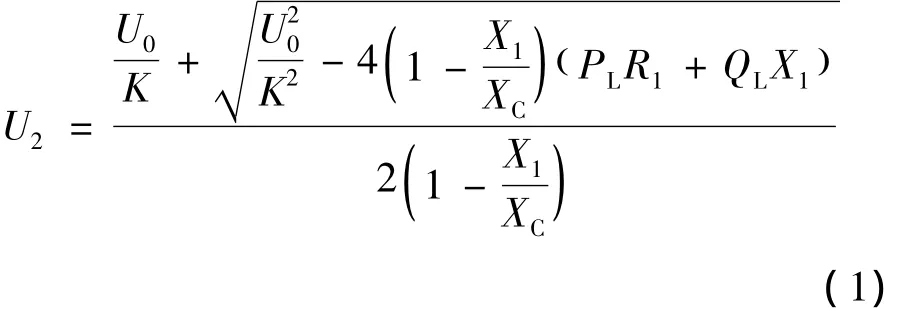
式中:R1和X1分别为归算至子级变电站主变二次侧的等效电阻和电抗值，R1=R0/K2+RT，X1=X0/K2+XT;U0、X1、R1和X1为常数;U2与(PLR1+QLX1)、K和XC分别呈单调递减、单调递减和单调递增关系。

设g(PL，QL)=(PLR1+QLX1)，则U2可表示为

若使U2≥U2min，U2min为电压约束下限，则要求:

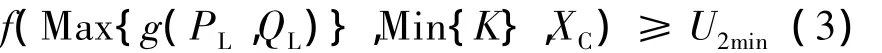
式中，Max{}和Min{}分别表示求取最大值和最小值。

2 地区放射电网无功补偿优化配置方法

根据上述方法可得地区放射电网无功补偿容量满足的约束条件，即

式中，XCmax为无功补偿最大容抗。

若XC值在0～XCmax改变，无功补偿投资成本和其所降低的网损电量也随之改变，下面分析如何在0～XCmax选取适当的XC，以达到综合考虑无功补偿投资成本和网损情况下电网运行成本的最小化。

两级变电站之间线路传输无功引发的有功损耗为

式中，R1为常数，传输无功引发的有功损耗ΔPQ大小与(QL－QC)2和U2相关，在电网运行过程中，通过合理调节变压器分接头和投切无功补偿电容可保证U2稳定在较小范围内，因此近似考虑U2为恒定值，则ΔPQ只与(QL－QC)2呈单调递增关系。统计某天QL变化如图3所示。

图3 QL日变化曲线Fig．3 QLday variety curve

由图3可知，QL时序变化曲线可反应各时刻负荷节点的无功需求，但无法为选择最优的无功补偿容量提供依据。

进行无功补偿容量规划时，应关注无功需求的总体变化规律，而不是关注具体的无功时序曲线。故可从QL持续变化曲线描述其变化规律，以此为依据选择最优的无功补偿容量。

统计1 aQL持续变化曲线如图4所示，点A表示1 a内QL超过11.15 MVA的累计时间不超过5000 h。

由图4可知，该母线无功负荷保持不小于7.8 MVA，所以需对其配置一定的无功补偿装置实现无功的就地平衡，以减小传输无功引发的有功损耗。

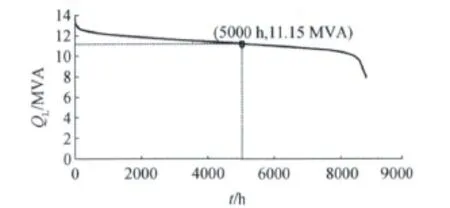
图4 QL持续变化曲线Fig．4 QLcontinuous variety curve

设配置n组额定容量为Qc.o无功补偿电容器，则无功补偿电容配置分析如图5所示。

图5 无功补偿电容配置分析图Fig．5 Configuration analysis chart of reactive compensation capacitor

图 5 中，t1和t2分别为QL超过nQC．o和(n－1)QC．o的累计时间。此时电网传输无功引发的有功损耗ΔPQ主要包括两部分:1)无功补偿容量不足引发的ΔPQ;2)无功补偿容量非连续变化引发的ΔPQ。下面具体分析其大小。

配置n组额定容量为Qc．o无功补偿电容器，部分QL大于nQc．o，以致不能实现无功就地平衡，从而需由电源端供给部分无功，传输此部分无功所引发的有功损耗为

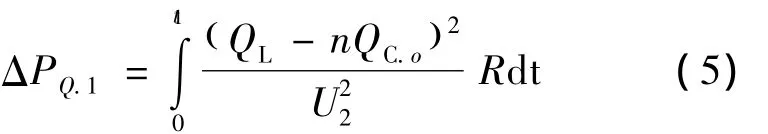
投切电容器过程中其无功补偿容量不能连续变化(如图 5 所示)，若无功负荷在(n－1)QC．o至nQC．o之间变化，虽然无功补偿容量满足最大无功负荷需求，但QL≠QC，则由式(4)可知会由此引发一定无功损耗:

同理可求得无功负荷在(i－1)QC．o至iQC．o之间变化时传输无功所引发的有功损耗，其中1≤i≤n，将其累加可得:

设电价为λ，则最终线路传输无功功率导致的电量损失成本为

设单组无功补偿电容器投资成本为α，运行年限为m，则平均每年无功补偿电容的投资成本为

优化配置无功补偿电容的目标是使Π1与Π2之和最小，即电网相应的总运行成本Π最小:

通过摄动无功补偿电容器配置组数n的大小，结合式(5)—式(6)可求得相应的最优配置组数。

3 算例分析

基于某地区实际电网结构及1 a的运行数据，通过算例分析所设计的无功补偿电容优化配置方法对降低电网运行成本的有效性，并计算该地区220 kV变电站下属子级变电站无功补偿电容的最优配置容量。该区系统接线如图6所示。

图6 220 kV变电站下属区域系统接线图Fig．6 System wiring diagram in 220 kV substation subordinate regional

1号变电站1 a的有功负荷和无功负荷曲线分别如图7、图8所示，2号—6号变电站有功负荷和无功负荷曲线如图9所示。电价和无功补偿电容技术经济参数如表1所示。

图7 1号变电站有功负荷曲线Fig．7 No．1 substation active power load curve

图8 1号变电站无功负荷曲线Fig．8 No．1 substation reactive load curve

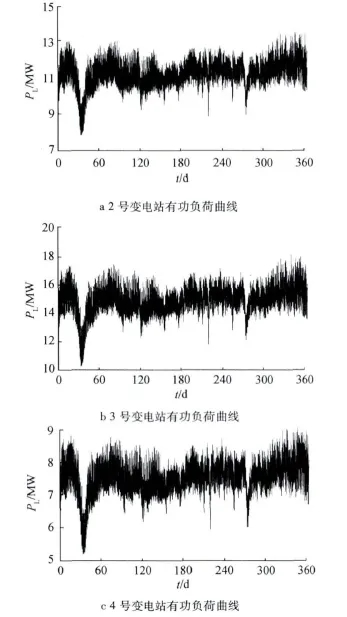
图9 2号—6号变电站有功负荷和无功负荷曲线Fig．9 No．2 －No．6 substation active power load and reactive load curves

表1 电价和无功补偿电容技术经济参数Tab．1 Price and economic parameters of reactive power compensation capacitor technology

根据1号变电站1 a的无功负荷统计，其无功负荷持续曲线如图10所示，QLmax为最大无功负荷。根据公式(1)—式(3)求得相应的无功补偿最大容抗为+∞，即使1号变电站母线满足电压约束条件，也无需对其配置无功补偿电容。由此可知，在0～QLmax可选择最优的无功补偿容量，实现经济上最优。

图10 1号变电站无功负荷持续曲线Fig．10 No．1 substation reactive load continued curve

在0组—28组选择无功补偿电容器配置组数，然后绘制相应的网损电量成本Π1、平均每年无功补偿电容投资成本Π2和电网相应的总运行成本Π变化，如图11所示。

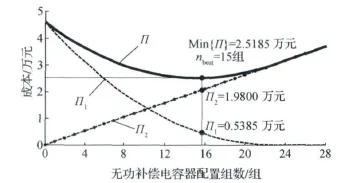
无功补偿电容投资成本随着其配置组数的增加而线性增加，而此时更多的无功可完成就地补偿，减小了传输所引发的无功损耗，因此相应的网损电量成本不断减小。当无功补偿电容器配置15组时达到了电容器投资成本和相应网损电量成本两者之间的权衡，实现了相应总运行成本的最小化，最小成本为2.5185万元，此时平均每年无功补偿电容器投资成本为1.9800万元，相应的网损电量成本为0.5385万元。

计算220 kV下属各变电站无功补偿最优配置如表2所示。

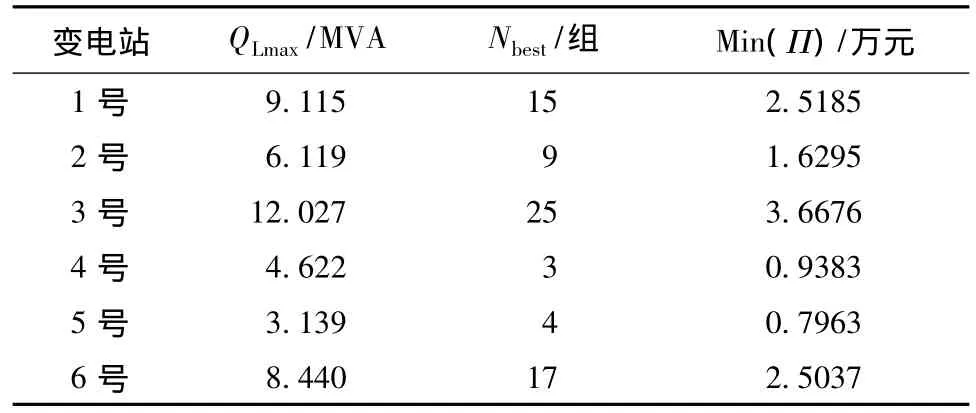
表2 220 kV下属变电站无功补偿最优配置Tab．2 Optimal configuration of reactive power compensation in 220 kV subordinate substation

由表2可知，变电站无功补偿电容最优配置容量随着最大无功负荷的增加而呈增大趋势，因此电网相应的总最小成本也呈增加趋势。

4 结论

1)基于综合考虑无功补偿电容投资成本和网损成本基础上，提出了一种无功补偿电容的优化配置方法，可权衡网损造成的经济损失;设计的地区电网无功补偿容量，可降低电网相应的运行成本。2)随着变电站无功负荷的增加，对其配置的最优无功补偿容量和电网相应的总最小运行成本呈增加趋势。

［1］丁玲，谢国强，宋嘉峰．风电场接入通辽电网后的系统潮流和无功电压研究［J］．黑龙江电力，2012，34(1):57-61．DING Ling，XIE Guoqiang，SONG Jiafeng．Study on system flow wind farms connected to the power grid of Tongliao and reactive voltage［J］．Heilongjiang Electric Power，2012，34(1):57-61．

［2］杨龑亮．改进粒子群算法的无功优化［J］．黑龙江电力，2011，33(1):33-36．YANG Yanliang．Reactive power optimization for the improved particle swarm optimization algorithm［J］．Heilongjiang Electric Power，2011，33(1):33-36．

［3］孙毅，李欣．基于全局粒子群算法的无功优化［J］．黑龙江电力，2011，33(1):69-71．SUN Yi，LI Xin．Reactive power optimization based on global particle swarm optimization algorithm［J］．Heilongjiang Electric Power，2011，33(1):69-71．

［4］张永昕，申强，张俊文，等．无功补偿设备在电力系统中的应用分析［J］．黑龙江电力，2008，30(1):70-72．ZHANG Yongxin，SHEN Qiang，ZHANG Junwen，et al．Analysis of the application of reactive power compensation device in power system［J］．Heilongjiang Electric Power，2008，30(1):70-72．

［5］刘传铨，张焰．电力系统无功补偿点及其补偿容量的确定［J］．电网技术，2007，31(12):78-81．LIU Chuanquan，ZHANG Yan．Determination of power system reactive power compensation point and capacity［J］．Power System Technology，2007，31(12):78-81．

［6］李红兵．AVC浅析供区网络无功潮流在无功补偿增配需求分析中的应用［J］．湖北电力，2009，33(3):26-27．LI Hongbing．AVC Analysis of application of district network reactive power flow in additional demand compensation［J］．Hubei Electric Power，2009，33(3):26-27．

［7］陈刚，马爱军，张继红，等．AVC分散控制模式下的变电站电压无功控制研究［J］．电网技术，2010，34(12):187-192．CHEN Gang，MA Aijun，ZHANG Jihong，et al．AVC study on reactive power control of substation with distributed voltage control mode［J］．Power System Technology，2010，34(12):187-192．