用于SFBC MIMO－OFDM系统的改进SLM算法*

罗仁泽，李芮，杨 娇，牛娜

(西南石油大学电气信息学院，成都 610500)

在设法采用SLM算法降低Alamouti方案MIMO－OFDM系统的峰均比时，由于对信号进行空频编码后使信号具有一定正交性，独立应用SLM算法，会破坏SFBC编码的正交特性。考虑相位序列间的对应关系，由于空频编码是在两个相邻载波间，所以此处只考虑一对相邻子载波［X(m)，X(m+1)］，经过空频编码后输出为

1 引言

MIMO－OFDM系统中核心技术之一为空频编码(SFBC)，在多个发射天线的信号之间采用空频编码后，信号将产生空域、频域的相关性。通过该编码的应用，MIMO－OFDM系统可以利用空间和频率的分集提高数据传输率，增加系统的容量和传输的可靠性。然而，由于MIMO－OFDM系统中的OFDM符号是由多个独立且经调制的子载波信号叠加而成的，当载波间相位相同或相近时，信号的叠加会产生瞬时功率峰值，进入功率放大器的非线性区时会进一步引发信号畸变，这将严重影响系统的性能。

在MIMO－OFDM系统中，解决其峰均功率比(Peak－to－Average Power Ratio，PAPR)问题的方法可概括为两个方面。一方面是将OFDM系统中常用方法直接移植到MIMO－OFDM系统的每一根天线上。目前，已经提出的降低OFDM系统峰均比的技术有三类:第一类是信号预畸变技术，最常见的信号预畸变技术包括限幅［1］和压扩［2］等算法，在信号经过放大前，要经过非线性处理;第二类是编码技术［3］，原理是利用不同的编码原理避免产生较高PAPR的码字出现;第三类是扰码技术，该方法利用不同的加扰序列对OFDM符号进行加权处理，显著减小大峰值功率信号出现的概率，其中扰码类中如选择映射(SLM)法［4］和部分传输序列(PTS)法［5］因其性能较好已被广泛应用于OFDM系统中。另一方面是针对MIMO－OFDM系统的本身特性，采取更为有效的方法。如Yung－L Lee提出的并行SLM算法［6］，在发射端采用同种旋转序列矢量调制，可减少辅助信息量，但它是以牺牲部分PAPR为代价。由M.Tan等提出的降低STBC MIMO－OFDM系统PAPR的交叉天线旋转取反(CARI)算法［7］，有效利用天线之间的附加空间自由度，改善了系统的峰均功率比。该算法与并行SLM算法相比具有良好的峰均比性能，且每次迭代不需要大量的复乘运算，降低了计算复杂度，但是随着发射端天线数的增加，直接拓展反而更增加了系统的复杂度，且不能获得PAPR的进一步改善。文献［8］提出的SFBC MIMO－OFDM系统中，结合SLM算法提出了一种只需采用少量IFFT的低复杂度算法，正是由于缺少IFFT的次数，系统不能获得良好的PAPR性能。

为了降低MIMO－OFDM系统的峰均功率比和计算复杂度，本文构造了F矩阵，提出了一种基于F矩阵的SFBC MIMO－OFDM系统改进SLM算法，降低了系统峰均功率比和计算复杂度。该方法巧妙利用MIMO系统中基于SFBC编码后天线上信号的正交性，利用构造的F矩阵对编码信号进行独立处理，获得的最优相位序列取共轭，以共轭序列中每两个旋转因子为一个单位交换位置，扰码空频编码的信号，减少每根天线上IFFT次数，从而降低系统计算复杂度，同时F矩阵的使用也让系统获得了良好的峰均比性能。

2 SFBC MIMO－OFDM系统及其PAPR

考虑N(N≥4)根发射天线的 SFBC MIMOOFDM系统，在发射端输入的信息流，首先经过PSK/QAM调制映射，映射后的数据流串行进入空频编码器进行MIMO编码，经过空频编码之后的信息流变为并行数据流，每路数据流分别对应一根发射天线。对N=4根天线分别进行OFDM调制，包括串并转换、插入导频、IFFT运算、并串转换、加入循环前缀，最后送入D/A变换，经过变频后由各天线发送出去。经过信道，接收端实行与发射端相反的操作，即可获得数据。SFBC MIMO－OFDM系统发射端基本框图如图1所示。

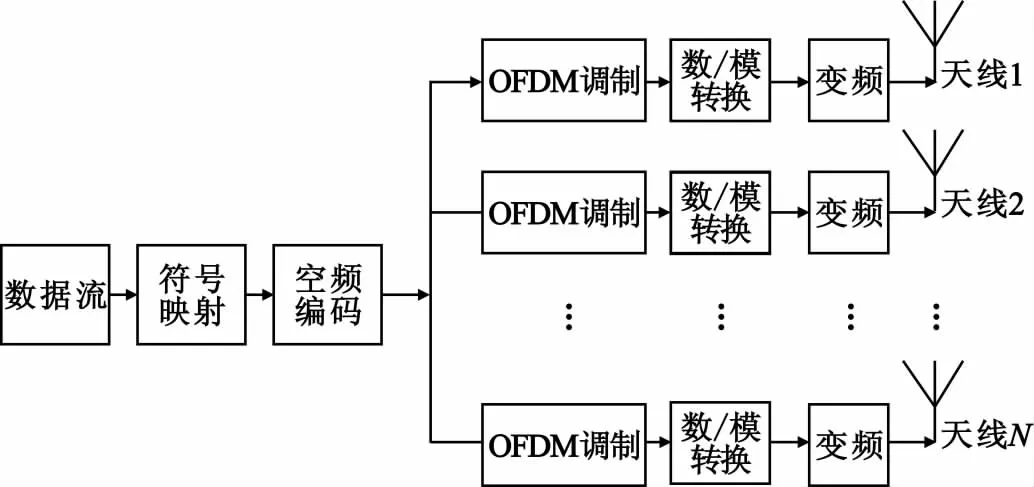
图1 SFBC MIMO－OFDM系统发射端基本框图Fig.1 Block diagram of the transmitter in SFBC MIMO－OFDM system

SFBC MIMO－OFDM系统使用OFDM调制方式，它继承了OFDM调制的众多优点，同时，也不可避免地存在较高的峰均功率比问题。对于一个具有N0个子载波的MIMO－OFDM系统，每根天线上的复数基带信号可表示为

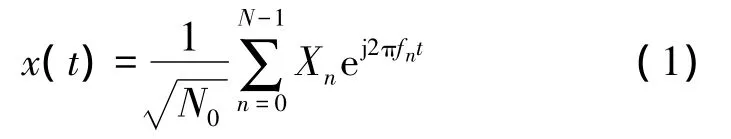
其中，0≤t≤N0T，fn=n×Δf表示每根天线上第 n 个子载波的频率，Δf=1/N0T，T为符号间隔。

MIMO－OFDM系统的峰均比定义为每一个MIMO－OFDM时域信号的峰值功率与该信号的平均功率的比值，表示为

或者，

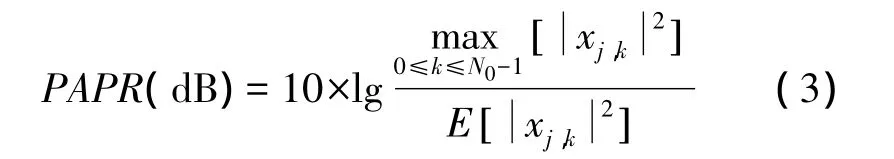
其中xj，k表示MIMO系统中第j根发射天线上载波序号为k的信号，且k∈(1，N0)，E［·］表示求数学期望。

3 基于F矩阵的改进SLM算法

为简化描述，算法采用天线数为2进行描述。图2是基于两根发射天线(N=2)的改进SLM算法系统框图。

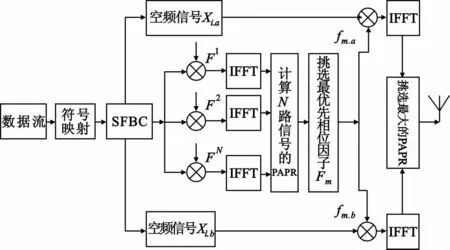
图2 基于SFBC的改进SLM算法系统框图(N=2)Fig.2 Block diagram of the improved SLM algorithm based on SFBC(N=2)

基于2×2天线的Alamouti方案中改进SLM算法描述如下:

输入二进制数据比特流，采用PSK/QAM进行调制，得到映射信号，经过串并转换后获得Xi频域信号，Xi表示第i个频域符号，

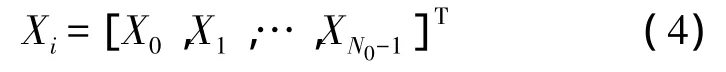
其中，N0表示子载波数，N×N的上限值设置为P(P＞0)，［·］T表示矩阵的转置;利用F矩阵产生初始相位序列组:

其中，k为衰减因子，I(N0)表示单位矩阵，N0表示子载波个数，rand(N0)表示随机产生的在(0，1)呈均匀分布的小数。采用SFBC对Xi信号进行正交编码，获得能在两根天线a、b上传输的空频信号，分别为 X'i，a，X'i，b，表达式如下:

天线a:

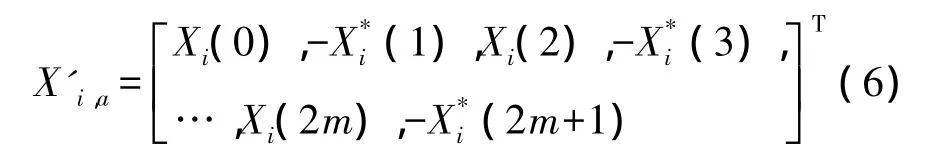
天线b:

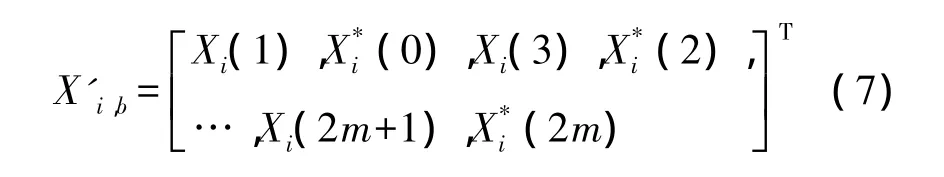
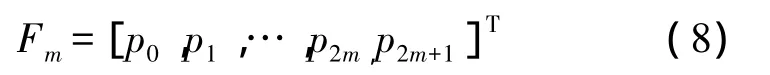
对该最优相位序列Fm取共轭记为，将序列中每两个旋转因子为一个单位交换位置，相位因子 fm，a=Fm，fm，b表达式如下:

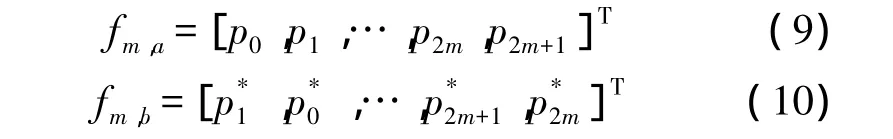
将两个相位序列分别作用于SFBC后的信号，上述变换不会影响SFBC编码的正交性。其中，相位序列 fm，a，fm，b分别对应信号 X'i，a，X'i，b;将上述所得相位因子与对应信号复乘，IFFT之后计算各自的PAPR值记为PAPRa和PAPRb，选取具有 max(PAPRa，PAPRb)的信号作为待发送信号cand()，添加保护间隔后信号为，通过天线将其发送出去。

4 算法理论分析

4.1 相位序列间的关系

在设法采用SLM算法降低Alamouti方案MIMO－OFDM系统的峰均比时，由于对信号进行空频编码后使信号具有一定正交性，独立应用SLM算法，会破坏SFBC编码的正交特性。考虑相位序列间的对应关系，由于空频编码是在两个相邻载波间，所以此处只考虑一对相邻子载波［X(m)，X(m+1)］，经过空频编码后输出为

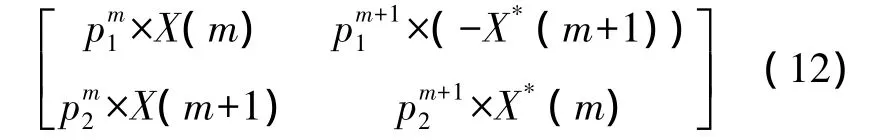
根据SFBC编码原理，要保持其正交性，则必须满足下式:

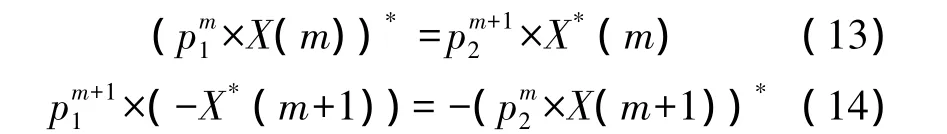
可以推导出

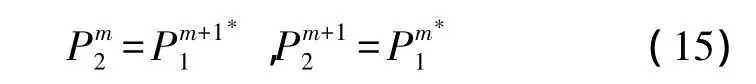
由此考虑N个子载波，可以得到两根天线相位序列的关系:

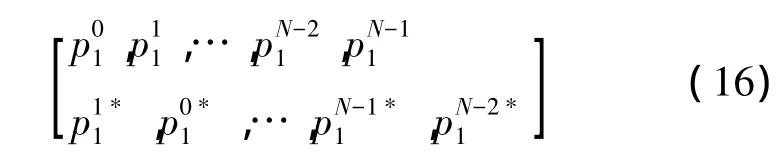
如此产生的相位序列不会破坏SFBC编码信号的正交性。

4.2 计算复杂度分析

F矩阵产生了M个相位序列，倘若直接将F矩阵作为SFBC后产生的两路信号的相位因子，采用基于STBC的并行SLM算法时［6］，每个符号在每根天线上需要做N次IFFT;若采用改进SLM算法，每个符号在每根天线上只需做1次IFFT。其计算量分析如表1所示，其中M表示相位因子数(F矩阵的维数)，N表示MIMO－OFDM系统的天线数，G表示一帧信号所包含的符号数。由此可以看出，并行SLM算法中采用大量 IFFT，而本算法在 MIMOOFDM系统多天线多载波调制的条件下，IFFT次数有明显降低，即计算复杂度降低了。

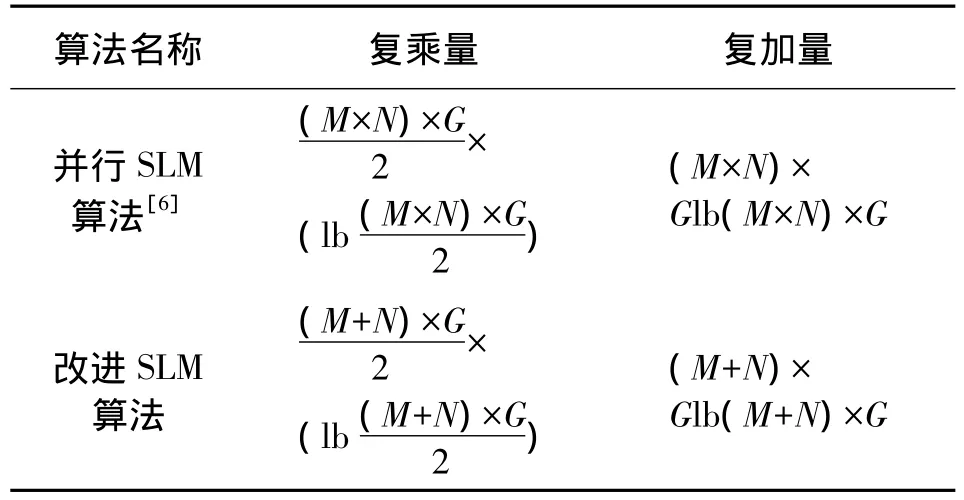
表1 不同算法的计算量分析Table 1 The calculation analysis of different algorithms

5 算法性能仿真及结果分析

此部分将对本文中提到的改进SLM算法进行仿真，采用Alamouti方案SFBC编码的MIMO系统，即发送天线数为2，仿真过程参数设置如下:子载波数 N0=128，系统采用过采样系数［4］L 为 4，二进制信号采用PSK调制，仿真次数为10000次。其中，发射天线数取2可简化多天线系统模型，方便实现SFBC编码，L≥4可以保证过采样后离散值更能接近于连续信号，但是L过大就会增加系统计算复杂度，此处选择L=4比较恰当。相同参数设置下，仿真过程中加入基于STBC的并行SLM算法［6］和相继次优［7］算法。

图3给出了不同算法下降低PAPR性能的比较，其中并行SLM算法中相位序列组数为v=4，相继次优算法中分块数目为M=4，改进SLM算法中衰减因子选择k=15。从图3中CCDF曲线看出，改进SLM算法较原始信号的 PAPR在10－3处有约3.5 dB的改善，而与相继次优算法比较在10－3处PAPR有约0.9 dB的改善，与并行SLM算法相比在10－3处有约1.8 dB的改善，由此可以得出 F矩阵的使用可以促进系统PAPR的进一步降低。

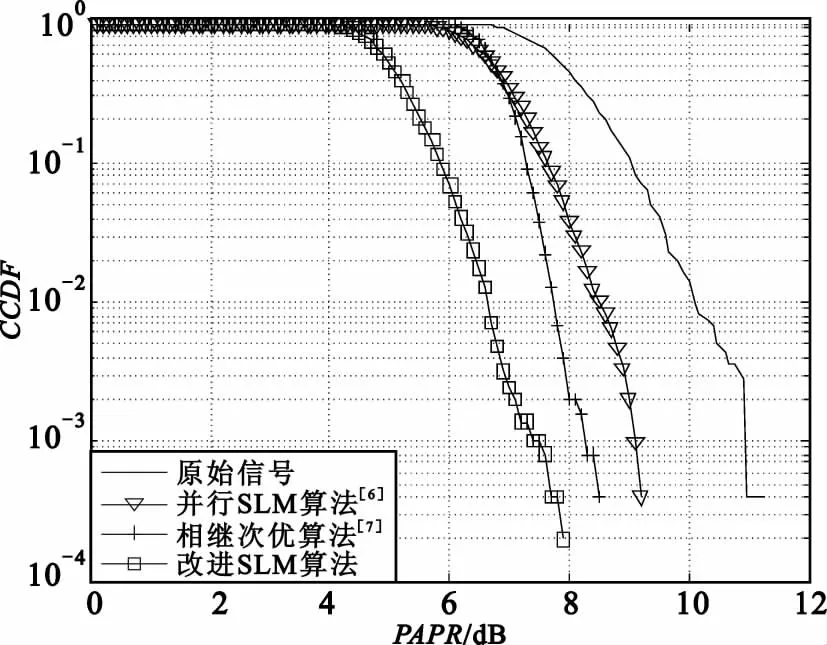
图3 不同算法降低PAPR的性能比较Fig.3 Comparison of PAPR reducing performance of different algorithms

图4给出了不同相位因序列组数v下的CCDF曲线。如图4，当 v=4时，CCDF曲线在10－3处，改进SLM算法较并行SLM算法PAPR有约4.8 dB的改善;当v=16时，改进SLM算法较并行SLM算法有约3 dB的改善。k值取定后，随着相位序列组数的增加，使得改进 SLM 算法在10－3处 PAPR有3 dB的改善，因此F矩阵用于降低PAPR具有较强的稳定性。

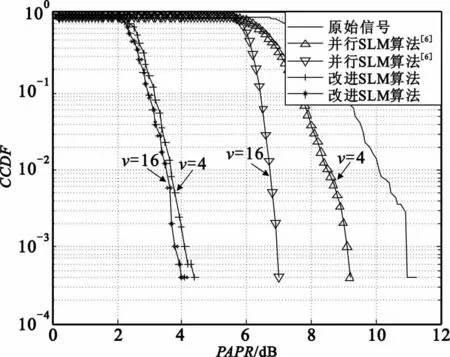
图4 不同相位序列组数v(相同的衰减因子k=5)的CCDF曲线图Fig.4 CCDF curve of different phase sequence v(same attenuation factor k=5)

图5是v=4，改进SLM算法在不同衰减因子条件下的CCDF曲线图。如图5，随着衰减因子的降低，PAPR也随之改善了。CCDF曲线在10－3处，k=7时，PAPR 约为5.5 dB;k=5 时，约为4.1 dB;k=2.5 时，约为2.4 dB;k=1 时，约为 1.3 dB。可见，F矩阵的应用改善了MIMO－OFDM系统的峰均比。

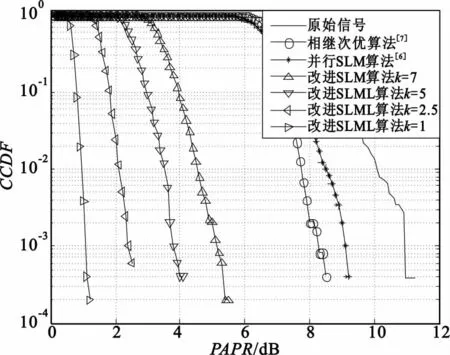
图5 改进SLM算法在不同衰减因子k下的CCDF曲线图Fig.5 CCDF curve of the improved SLM algorithm with different attenuation factor k

以上算法随着仿真次数的增加，曲线将更平滑，所获得的峰均比性能会更加稳定和可靠，但是仿真需要的时间也随之急剧增加，因此，在对仿真次数进行多次试验后，所有算法均采用了10000次仿真，从以上结果可以看出，算法性能在此条件下的改善也已经比较稳定和明显了。

6 结论

针对SFBC MIMO－OFDM系统中高 PAPR问题，构造了F矩阵并提出了一种基于F矩阵的改进SLM算法。经过严格的理论推导和Matlab仿真分析，与并行SLM算法和相继次优算法相对比，改进SLM算法创新之处在于能极大改善PAPR且计算复杂度大大降低。在MIMO－OFDM系统中，随着相位序列数的增加，边带信息的传输和存储将会成为一个难点，在该改进SLM算法的基础上进一步降低边带信息的传输方法是今后的研究方向。

［1］Wang Luqing，Tellambura C A.Simplified clipping and filtering technique for PAR Reduction in OFDM systems［J］.Signal Processing Letters，2005，12(6):453－456.

［2］姜晓俊，杨守义，穆晓敏，等.基于载波干涉和压扩技术的OFDM系统 PAPR降低算法［J］.电讯技术，2009，49(1):35－39.JIANG Xiao－jun，YANG Shou－yi，MU Xiao－min，et al.PAPR Reduction in OFDM Systems via Carrier Interferometry and Companding Transform［J］.Telecommunication Engineering，2009，49(1):35－39.(in china)

［3］Chen H，Liang H.PAPR Reduction of OFDM Signals Using Partial Transmit sequences and Reed－Muller Codes［J］.IEEE Communications Letters，2007，11(6):528－530.

［4］Jeon Hyun Bae，No Jong Seon，Shin Dong Joon.A Low－Complexity SLM Scheme Using Additive Mapping Sequences for PAPR Reduction of OFDM Signals［J］.IEEE Transactions on，2011，57(4):866－875.

［5］Li Li.Joint Decoding of LDPC Code and Phase Factors for OFDM Systems With PTS PAPR Reduction［J］.IEEE Transaction on Vehichlar Technology，2013，62(1):444－449.

［6］Lee Y L，YOU Y H，Joen W G.Peak－to－average power ratio in MIMO－OFDM systems using selective mapping［J］.IEEE Communications Letters，2003，7(12):575－577.

［7］Tan Mizhou，Latinovic Z，Bar－Ness Y.STBC MIMOOFDM Peak－to－Average Power Ratio Reduction by Cross－Antenna Rotation and Inversion［J］.IEEE Communications Letters，2005，9(7):592－594.

［8］Wang Sen Hung，Li Chih Peng.A Low Complexity PAPR Reduction Scheme for SFBC MIMO－OFDM Systems［J］.Signal Processing Letters，2009，16(11):941－944.