课堂上那一条无形的“线”
2014-03-04赵红婷
赵红婷
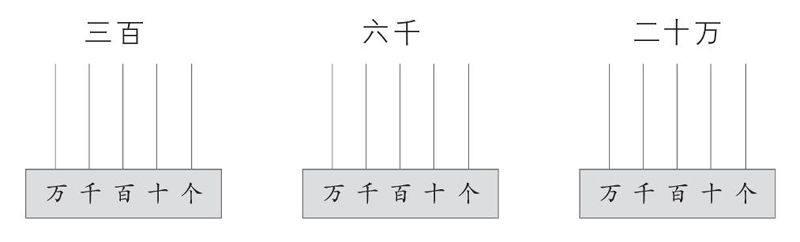
认识整万数,其实质是对数位结构的整体把握。从万以内数到整万数,这是认数的一次飞跃,也是数级的一次拓展。不管是认数、读数,还是写数,都与数位结构息息相关。课前,周老师设计了四个问题,引领学生开展小研究,课堂上的大多数时间,师生都在交流展示,看似随意,但形散而神不散,适时的点拨透露着深意。教师抓住了一条无形的“线”——数位结构,以数位结构的拓展、对应、分隔贯穿始终,使课堂教学达到了一定的深度。
一、拨数矛盾:实现数位结构的拓展
一位学生上台汇报交流小研究第1题。
生:我用画算珠的方法,在下面的计数器上表示相应的数。
学生呈现了前两个数拨珠方法,对于拨20万,她发现数位不够,就在旁边画了一根竖线,并在上面拨了两颗珠子。请别人补充,有学生说,新添的数位是十万位。
教师特意请该班冯博士同学上台展示小研究,他原本是在万位拨了20颗珠子,但上来展示时却已擦掉。教师及时抓住了这个例子,即使已擦去,仍让学生观察20颗珠子的印痕,学生认识到:如果万位上放20颗珠子,能表示20万。
教师设问:“万位上的20颗珠子,相当于十万位上的2颗珠子,它们之间是什么关系?”一学生说:“满十进一。”因而得出:万位和十万位之间的进率是10。教师说:“这两个计数单位只是冰山一角,能向左边看看,再向右边看看吗?”随着学生回答,教师板书了个级和万级的计数单位,并标出了相邻两个单位之间的进率。
【赏析】小研究第1题的设计,体现了教师的匠心独具。前两个数是复习旧知,第三个数意在激起矛盾,让学生感受数位拓展是必须。在最高位是万位的计数器上,拨20万,大多数学生都想到添加一个十万位。但教师并不满足于此,他发现一位学生的做法,即在万位上拨20颗珠子。在辨析中,使学生认识到:万位上的20颗珠子,相当于十万位上的2颗珠子,万位和十万位之间的进率是10。随着数的位数逐渐增多,新的数位将不断出现,教师顺势引导学生从个级数位拓展到万级数位,原有的数位结构便得到拓展和更新。
二、写数对比:凸显数位结构的对应
一位学生上台交流第2个研究问题,具体如下。
师:怎么写整万数呢?结合下面的例子介绍我的方法。
例如,南京市目前常住人口大约是八百万人,这个数写作________________________________________________。
这个数写作:________________________________________________ 。
我的方法是:________________________________________________。
这个学生举的例子是:武汉大约有人口一千三百万,写作:13000000。他的方法是:先写1300,再写四个0。另一学生上台补充:一套豪华别墅一千万,写作10000000。她的方法是:先写后面的四个0,再写前面的数。教师肯定了两位学生的做法,鼓励学生上黑板贴出数位,并写出八百万和一千万。
接着,教师报数,学习练习写数,依次是如下各数:
八十五 八十五万
八百五十 八百五十万
八千五百 八千五百万
教师:“从左往右看,你是不是有话说?”学生:“右边数比左边数多4个0。”教师:“多了个‘万字,就多了4个0。从上往下看,有什么特点?”学生:“右边的数都有四个0。”揭示整万数后,教师又追问:“整万数末尾都只有四个0吗?”学生持反对意见,学生:“不是,整万数可能有4个0。”师生经过互相争论和补充,得出:凡是整万数末尾至少有4个0。
【赏析】小研究的第2题重在研究写数方法。学生掌握写法后,教师组织学生进行写数对比。横向对比使学生意识到,后者只比前者多一个“万”,写数的前一部分都是一致的,后者只要多写4个0。纵向对比,学生更清晰地认识到,右边是整万数,它们末尾至少有4个0。这样的纵横对比,沟通了个级与万级数位的联系,虽然数级不同,但相关数位的对应关系却是一致的。学生虽未能言传,但他们已隐约意识到,整万数前一部分的书写,跟万以内数的写法是一致的,只需在后面添4个0即可。凸显数位结构之间的对应关系,对学生认数、写数都至关重要。
三、读数求简:突出数位结构的分隔
学生上台汇报小研究的第3个问题,具体如下。
生:怎么读这个整万数呢?结合下面的例子介绍我的方法。
例如:一辆奔驰车的价格是1240000元,这个数读作:________________________________________________。
________________________________________________。
我的方法是________________________________________________。
一位学生上台读出了汽车的价钱,举出自己的例子,并介绍了自己的方法:先读前面的数,再读万。
教师:“怎样读数更简便呢?”教师特意请另一位学生上来交流,他说:“只要在千和万之间画一条竖线,我一看就知道了!”教师:“这样画竖线好吗?画竖线是不是随便画的?几个0才能换一个万?”师生交流后得出:在千位和万位之间画一条竖线,这便是个级和万级的分级线。
【赏析】小研究的第3题主要解决读数问题。对学生而言,读数的难度要比写数更大,因为读数首先要将整万数进行分级。教师并未直接介绍数位的分级,而是让学生在读数中感受分级的必要性。在师生的交流补充中,学生达成共识:要在千位和万位之间画分级线。事实上,分级线看似细小、微不足道,但对于构建正确的数位结构,起着非常关键的作用。数位的分级是一种分隔,但更是一种统整,分级线虽将个级和万级予以区分,但其潜在的对应关系却愈加分明,因此,分级既有分的思想,更有合的韵味。
四、玩数活动:内化数位结构的特质
学生上台交流小研究的第4题,题目如下。
认识“整万数”这部分内容中,有的题目特别好,我来给大家推荐一道。(可以从课本或资料中找现成的,也可以自己编)
解决了两位学生设计的题目后,教师请几位学生参与摆数游戏,用9、5、3、0、0、0摆一个整万数,呈现:953000。教师:“你们有什么想说的?”学生:“少了一个0。”教师给出两个0,学生贴出:95300000。教师:“只能这么摆吗?”学生又将数改为:59300000,39500000。教师提示:后面的5个数能动吗?于是,学生摆成:39050000。教师:“动来动去,有的地方一直没动,哪些数不能动?”学生发现,最后四个0没有动。教师鼓励学生摆出一个最大的整万数和一个最小的整万数。学生都很容易摆了出来,接着教师说:“允许有些数字卡片下岗,摆出最小的整万数。”几位学生颇费了些周折,先是呈现了3050000,最后终于大胆摆出了30000。
【赏析】第4个小研究题目,旨在鼓励学生与教师一起设计或搜集题目。解决了两个学生的典型题目后,教师跟学生做起了摆数游戏。一开始,教师故意给学生6张数字卡片(其中仅三个0),学生马上发现少了一个0,此处再次强化:整万数的末尾要有4个0。接下去,教师给了学生两个0,学生贴出一个最大的整万数后,教师鼓励学生改变数。教师问:“动来动去,有的地方一直没动,哪些数不能动?”这个问题极为绝妙,让学生再次感受到整万数的数位结构,即整万数末尾至少要有4个0。接着,教师鼓励学生让一些卡片“下岗”,最后呈现“30000”,再次凸显:整万数末尾至少要有4个0。这是整万数最显著的特征,教师通过一个摆卡片游戏,将整万数数位结构的特征再次凸显,收到了意想不到的效果。
(作者单位:江苏省张家港市云盘小学 责任编辑:王彬)
