基于改进的QPSO-BP算法的锌矿价格行情预测
2014-03-04江龙艳
江龙艳
(湖南万源评估咨询有限公司,长沙410007)
我国是一个锌矿资源十分丰富的国家,也是世界上锌生产和消费的大国[1]。随着我国现代化进程的加快,锌的应用范围和需求量也不断扩大和增加。锌的价格变化直接影响了人民生产和生活的各个领域。因此,分析锌市场价格变化情况,预测锌产品价格变化趋势,对减小锌价格变化对锌行业的负面影响,保障国民经济快速发展有重要意义。
目前,国内专门针对锌价格预测的研究还很少。但针对矿产品、现货价格预测,国内研究人员做了大量研究。孙继湖、王立杰等[2-3]建立ARIMA时间序列模型,将随机论、概率论、线性差分方程应用到煤炭市场价格预测,对煤炭价格的未来走势进行分析和判断。魏毅等[4]提出采用灰色预测模型对煤炭价格指数在中、短期的变化进行预测。郭熊娃等[5]利用WTI原油现货价格月度数据 ,将分数阶差分与非参数自回归模型相结合,建立了WTI原油现货价格序列的基于分数阶差分的非参数自回归预测模型。这些模型方法都可以引用到锌价格变化趋势预测中,但是时间序列建模时,随机扰动项的非高斯性质造成传统的时序模型的估计和预测偏误[6];利用灰色系统和回归模型对锌价格进行预测时,都存在预测精度不高、误差较大的情况。
随着人工智能技术的发展,研究者开始将BP神经网络的方法运用于价格预测中,曾濂、顾孟钧等[7-10]提出一种改进的BP神经网络建立黄金期货价格仿真预测模型;张坤、丁睿等[11-12]利用改进的神经网络,预测了国际铀资源的价格变化。这些方法对锌价格预测的研究有着很好的启发作用。但是利用BP神经网络进行锌价格预测时,存在无法确保是否收敛到了全局最小点及收敛速度慢等问题。因此本文以2008年11月至2011年10月我国南方锌精矿价格统计数据为基础,引入改进的量子粒子群算法(QPSO)对BP神经网络训练方法进行优化,提高了预测结果的精确度和预测过程的稳定性,为锌资源的开发利用和回收投资提供了科学的参考依据。
1 基于改进的量子粒子群算法优化神经网络训练方法
1.1 基于改进的量子粒子群优化算法
量子粒子群优化(Quantum-behaved Particle Swarm Optimization)算法[13]是一种基于群智能全局优化的技术,在量子空间中,粒子聚集性是通过其运动中心的吸引势产生的束缚态进行描述的,束缚态下的粒子以一定的概率密度在空间任何点出现,满足聚集态的粒子能在整个可行解的空间进行搜索,且不会发散至无穷远处,从而找到最优解。
基于δ势阱的量子粒子群算法(QPSO)首先用波函数Ψ(X,t)来描述粒子的状态,其中,X为粒子i的三维空间位置向量,波函数的模的平方等于粒子在空间中某一点出现的概率密度。然后采用逆变换法(蒙特卡罗法)得到粒子的位置方程:

式中,t—离散时间;L—δ势阱的特征长度;收敛点p在实际的算法运行中为随机变量;u(t)在(0,1)上的均匀分布。
将上述结果扩展到N维的搜索空间,对于粒子i(粒子位置坐标xi,j,j=1,2,…,N),第j维的坐标的基本进化方程为:

文献[15]证明了N维空间中,单个粒子的位置收敛性可归结为一维空间粒子的收敛性。引入平均最好位置(mean best position)C(t),

则粒子的进化公式为:

其中,Li,j(t)=2a|Cj(t)-Xi,j(t)|。α为扩张—收缩因子,它是QPSO算法除了种群规模和迭代次数外,唯一的参数。
传统QPSO将参数α随时间变化,从1线性减小到0.5。随着时间t的增加,粒子经历个体的最优位置pbest逐渐接近群体最佳位置gbest,平均最好位置mbest与每个粒子位置的差距也将逐渐变小,导致粒子实际搜索范围减小,粒子群进化趋于停滞。本文采用文献[14]提出的方法,将α从0.6增加到0.9,延缓整个粒子群存在的早熟趋势。

其中,maxiter为最大迭代次数。
在算法的搜索后期,即使α增加至0.9,仍有粒子所经历的pbest与gbest十分接近,导致δ势阱的特征长度L很小。因此,针对每个粒子,本文采用文献[15]中的第二种方法,对参数L进行改进。
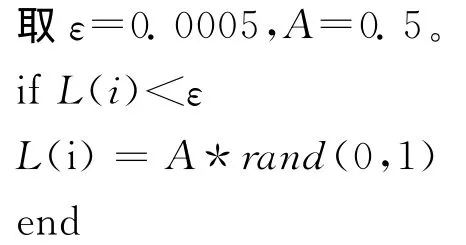
1.2 BP神经网络
BP神经网络是一种基于误差的反向传递(back propagation)算法。结构如图1所示。

在训练BP网络时,给定样本输入向量I,实际输出向量D可以表示为:式中,W—链接权值的矩阵;V—阈值向量;f—S型函数或者线性函数。
给定目标输出向量T,将误差函数作为适应度函数fitness,可表示为:

式中,P—样本总数;N—输出节点数,di,j、ti,j分别是第i个样本的第j个输出节点的实际输出和目标输出。
神经网络外推能力用泛化能力来进行评价。泛化能力是指衡量预测值与实测值之间差别的变量,用平均相对变动值 (Average Relative Variance,ARV)表示[16],ARV值越小,网络泛化能力越强。

式中,N—检验样本数;x—实际值;x~—实际值;x-—平均值。
1.3 基于改进的QPSO-BP算法流程

图1 BP神经网络的拓扑结构Fig.1 Topology of BPneural network
BP神经网络学习的过程主要是权值和阈值更新过程,将网络权值与阈值编码成粒子群位置向量,则每一个粒子代表了网络的一组权值与阈值,以误差函数作为改进QPSO算法适应度函数,通过优化搜索得到满足适应度函数值最小的一组粒子,即为训练网络的一组最优的参数。其基本流程[16-17]为:
1)给定输入向量和期望输出向量
(1)数据划分。采用滚动的方式对样本进行重构,即前N个值来预测后M个原始序列的值。数据划分方法见表1。

表1 数据划分Table 1 Data partition
(2)原始数据序列x(t)归一化。min(t)与max(t)分别是数据序列中的最小值与最大值。

2)确定神经网络输入层、隐含层、输出层节点数;
3)粒子群初始化。设定粒子数M,粒子向量X的长度L、目标适应度值fitness、最大迭代次数maxiter和粒子速度向量维数D。
(1)粒子数。对于一般优化问题,粒子数取20~40即可得到较好的结果。
(2)粒子向量X的长度L。计算公式为L=(s1+s3)×(s2+1),其中,s1为输入样本的维数,s2为隐含层节点数,s3为输出结果维数。
(3)粒子维度。其值与神经网络的连接权值与阈值有关,计算公式为D=w+v+h+n,w=m×h,v=h×n,其中,D为速度向量的维数;w为输入层到隐含层的连接权值的个数;v为隐含层到输出层的连接权值的个数;m为输入层节点数;h为隐含层节点数;n为输出层节点数。迭代次数N初始值为1。
4)适应度函数的确定。用公式(6)计算适应度函数fitness,来评价粒子的搜索性能。
5)当种群的最优适应度值满足目标适应度值或达到最大迭代次数时,学习过程结束;否则,令N=N+1,返回步骤(4)继续迭代。
6)设置网络的训练误差最大值g。若fitness>g,则采用所得连接权值与阈值作为网络训练的初始值,然后用训练好的网络对新输入的样本进行预测;若fitness≤g则直接对新样本数据进行预测。
2 基于量子粒子群优化的神经网络在锌矿价格预测中的应用
在MATLAB R2010a的环境中进行试验,为了提高预测的效率,将训练与预测过程设计成一个程序。数据来自南方50%锌精矿2008年11月至2011年10月的价格统计,见表2。
2.1 构建模型
将表2样本集的数据,按照表1进行数据划分,令N=3,K=28,M=1,分为30个长度为4的数据段,按公式(8)对数据进行归一化处理;网络输入节点数为3,根据隐含层数量公式:ni=2n+1,选择隐含层节点数为7,输出节点为锌价预测值,因此,网络结构为3—7—1型;训练和测试网络的过程中,训练样本的组数越多,可以提高网络的预测精度,即前35组数据作为训练的样本,后3组数据作为测试的样本。将样本处理后输入至网络进行训练。
2.2 QPSO优化BP网络
由神经网络5-11-1型结构确定需要优化的参数为1 560个,即

取粒子数目为20,粒子向量X的长度L为66,粒子速度向量维数为78;最大迭代步数100。参数优化过程如图2所示。优化后的粒子位置向量、由向量解码成的网络权值、阈值如下:

表2 预测模型的训练样本Table 2 Training Samples of prediction model


图2 适应度优化曲线Fig.2 Optimal curve of fitness

2.3 预测结果
将用QPSO优化后的网络参数代入BP神经网络,作为参数的初始值,满足训练精度或最大训练次数后,进行预测。从表3中可以看出,模型预测结果的相对误差的绝对值最大为2.54%,最小为0.006%。预测结果较好,但是具有一定的随机性。

表3 QPSO-BP模型预测结果Table 3 Prediction results of QPSO-BP model
为了进一步检验QPSO-BP模型在预测中的有效性,采用平均绝对百分比误差(mean absolute percentage error,MAPE)来衡量预测精度。另外做了2组试验(参数设置见表4),分别用2种模型进行预测,每组10次。

表4 PSO与QPSO参数设置Table 4 Parameter setting of PSO and QPSO

图3 QPSO适应度优化曲线Fig.3 Fitness optimal curve of QPSO

图4 PSO适应度优化曲线Fig.4Fitness optimal curve of PSO
对比2种网络预测结果(表5,鉴于篇幅有限,只列出每个模型每组的第一个预测值)与多次试验的结果(表6)。结果表明,试验1QPSO-BP模型的MAPE均值为 0.0100 7%,最大精度为 0.0198 4%。试验2PSO-BP模型的MAPE均值为0.041 844 078%,最 大 精 度 为 0.069 891 626%。显 然,QPSO的预测精度较好。
模型的泛化能力按公式(7)可以计算出PSO-BP,QPSO-BP模型的ARV分别为2.907 4,0.002 5。未进行优化的BP模型需要较多的迭代次数进行权值与阈值的更新,泛化能力较差;而ARV值QPSO-BP模型远远小于PSO-BP模型,因此,QPSO-BP模型的泛化能力最强。

表5 QPSO与PSO模型预测值比较Table 5 Predictive value comparison between QPSO and PSO model
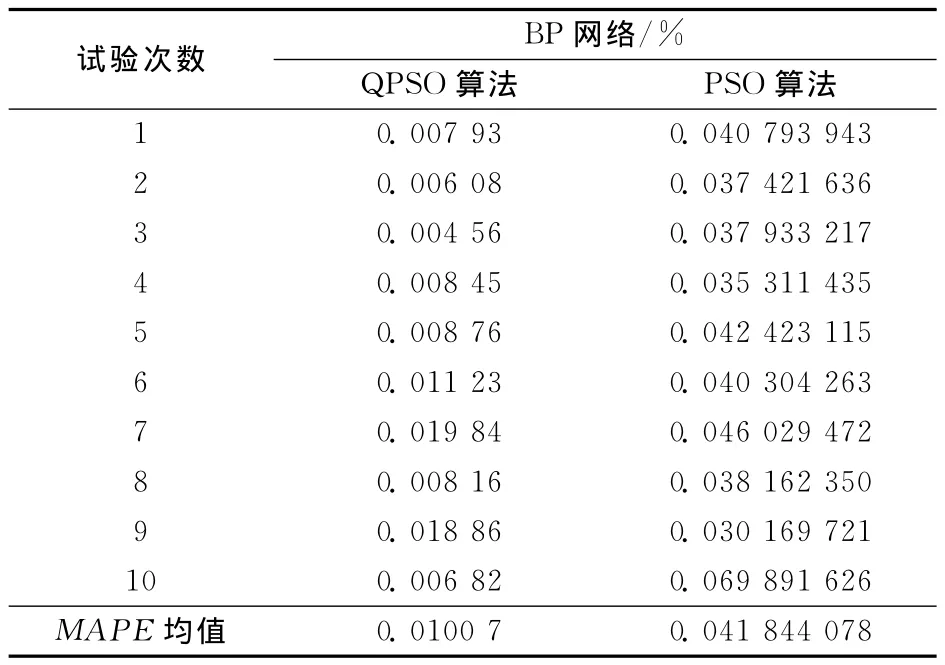
表6 QPSO与PSO模型MAPE比较Table 6 MAPEcomparison between QPSO and PSO model
3 结论
1)建立锌价格QPSO-BP模型的历史数据是在各种相关因素的宏观作用下形成的,可认为经济因素具有相对稳定性,变动趋势以及对锌价格影响规律短期不变,利用锌价格的历史数据进行短期预测能保证一定的精度。
2)用量子粒子群算法优化BP神经网络的学习算法,建立改进的量子粒子群BP模型,对网络的初始权值与阈值快速优化,在一定程度上能解决粒子群早熟、网络收敛速度慢、容易陷入局部最优的问题。
3)利用上述模型对锌价格进行预测,精度高于传统BP模型与粒子群优化BP模型,能较好地解决锌价格预测精度的问题;泛化能力指标平均相对变动值为0.0025,泛化能力高;相对误差分布集中,预测结果稳定。
4)锌产品价格的变化直接决定了锌矿项目的价值,采用改进QPSO-BP模型能对锌价格进行精确预测,降低矿业投资决策的风险,还可用于类似的矿产品的价格预测,应用前景广阔。
[1] 赵翠青 .当前中国锌工业的发展形势与思考[J].中国金属通报,2005(23):4-5.
[2] 孙继湖,彭建萍.时间序列分析技术在煤炭价格预测中的应用[J].地质技术经济管理,2000,22(3):33-40.
[3] 王立杰,刘志东.经济时间序列分析技术在煤炭价格预测中的应用[J].煤炭学报,2001,26(1):109-112.
[4] 魏 毅,程 跃,车永才.灰色理论在煤炭产品价格预测中的应用[J].中国煤炭,2006,32(6):19-21.
[5] 郭熊娃,张德生 .基于非参数自回归模型的WTI原油价格预测[J].山东理工大学学报:自然科学版,2012(12):69-73.
[6] 郭 帅,来 鹏 .时间序列混合模型及其在原油价格预测中的应用[J].南京信息工程大学学报:自然科学版,2010,2(3):280-283.
[7] 曾 濂,马丹頔,刘宗鑫 .基于BP神经网络改进的黄金价格预测[J].计算机仿真,2010,27(9):200-203.
[8] 顾孟钧,张志和,陈 友 .基于BP神经网络的国际黄金价格预测模型[J].商场现代化,2008(9):35.
[9] 徐向超,赵 瑞 .基于BP神经网络的世界黄金价格预测[J].科技情报开发与经济,2010,27(9):200-203.
[10] 张延利,张德生,刘常明,等 .基于BP神经网络的黄金价格非线性组合预测模型[J].黄金,2011,32(9):5-8.
[11] 张 坤,赵 玉 .国际市场中铀的价格变化规律及对我国核电发展的启示[J].东华理工大学学报:社会科学版,2011(4):315-317.
[12] 丁 睿 .基于神经网络的铀矿国际市场价格预测[D].长沙:中南大学,2009.
[13] 孙 俊 .量子行为粒子群优化算法研究[D].无锡:江南大学,2009.
[14] 王 鹏 .网络流量预测技术研究[D].无锡:江南大学,2009.
[15] SUN Jun.Adaptive parameter control for quantum-behaved particle swarm optimization on individual level[C]//IEEE International Conference on Systems,Man and Cybernetics,2005:3049-3054.
[16] 潘玉民,邓永红,张全柱,等 .基于QPSO-RBF的瓦斯涌出量预测模型[J].中国安全科学学报,2012,22(12):29-34.
[17] 刘成军,杨 鹏,吕文生,等.灰色—马尔科夫复合模型在黄金价格预测中的应用[J].有色金属(矿山部分),2013,65(1):7-11.
