一类具有阶段结构的时滞捕食系统稳定性分析

毕殿杰，孙玉涛，陈 涛

(安徽财经大学管理科学与工程学院，安徽 蚌埠，233030)

对于捕食系统模型的研究具有重要的理论意义和应用价值，能更好的解决生态学的问题。文献［1～6］提出的捕食系统模型都是假设捕食者对食饵具有相同的捕食能力，但是自然界中的大多数种群都经历从幼体到成年的一个成长过程，因此捕食者的捕食能力是变化的。但考虑到在某一阶段内，捕食者的捕食能力则是相对稳定的，因此具有阶段结构的捕食系统模型受到了众多研究者的关注［7～10］，这些模型也更贴近现实生态系统。在自然生态系统中，狩猎时滞这一因素对狩猎种群的繁衍会产生很大的影响，同时对食饵种群的繁衍也会产生很大的影响，因此引入该系统参数无疑更能有效的对系统状态进行反馈控制，更真实的反应现实。正因如此，近年来带有时滞性的阶段捕食系统成为一些学者研究的热点，文献［11～13］以不同的方法研究带有时滞性的阶段捕食系统的全局稳定性问题。文献［9］研究了如下具有阶段结构和Crowley-Martin功能性反应的捕食系统模型:

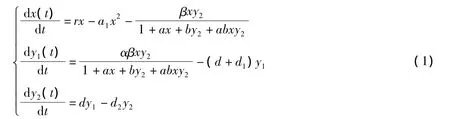
其中，x(t)为t时刻食饵的密度，y1(t)和y2(t)分别为t时刻幼年捕食者和成年捕食者的密度。a，a1，b，d，d1，d2，r，α与β均为正常数。其中，a表示捕食者的处理时间，b表示捕食者之间的相互干扰程度，a1表示食饵种群的种内竞争系数，d表示幼年捕食者到成年捕食者的转化系数，d1和d2分别表示幼年捕食者和成年捕食者的死亡率，r是食饵种群的增长率，β表示捕食者的捕获率，α表示捕食者的转化率。系统(1)虽然考虑到了捕食者的狩猎时间等因素，却忽略了狩猎时滞;由于捕食者从觅食到捕捉到食饵这一过程，均会有一定的时延，即一定会有狩猎时滞。基于系统(1)，笔者将捕食者的狩猎时滞引入到系统(1)得到如下时滞捕食系统模型:

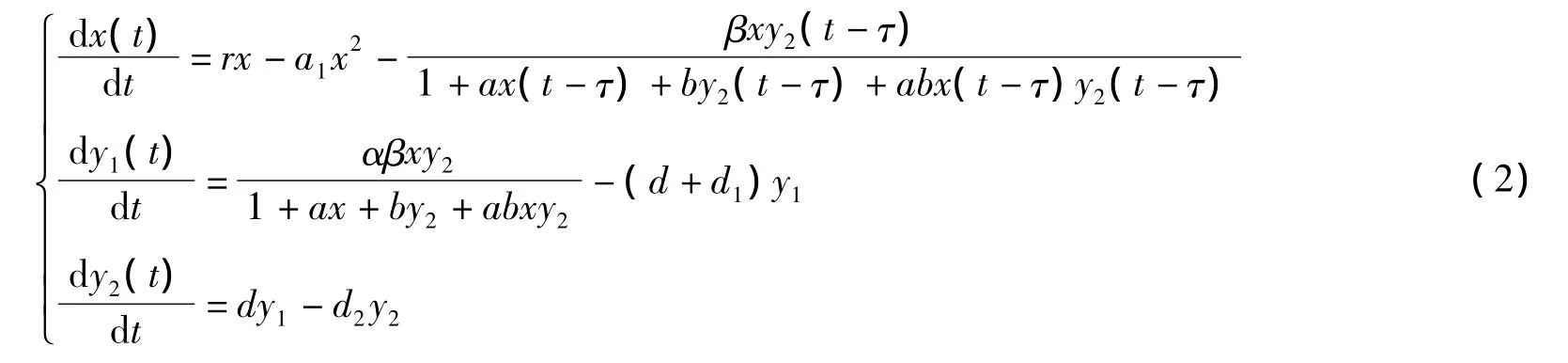
其中，常数τ≥0表示捕食者的狩猎时滞。基于系统的生态含义，笔者只在={(x，y1，y2)|x ＞0，y1＞0，y2＞0}内讨论系统(2)。

1 共存平衡点的稳定性和Hopf分支的存在性

所以，有下面的结果。

定理1.1 如果条件(H2)，(H3)和(H4)成立，那么

(i)当时 τ∈［0，τ0］，系统(2)的正平衡点 E*(x*，y1*，y2*是渐近稳定的;

(ii)当τ=τ0时，系统(2)在正平衡点E*(x*，y1*，y2*处产生Hopf分支。

2 仿真实例

令 r=3.5，a=0.0 1，a1=0.5，b=1.2，α =0.2，β =1 0，d=0.4，d1=0.8，d2=0.4 5，得到系统(2)的一个实例系统(1 0)。

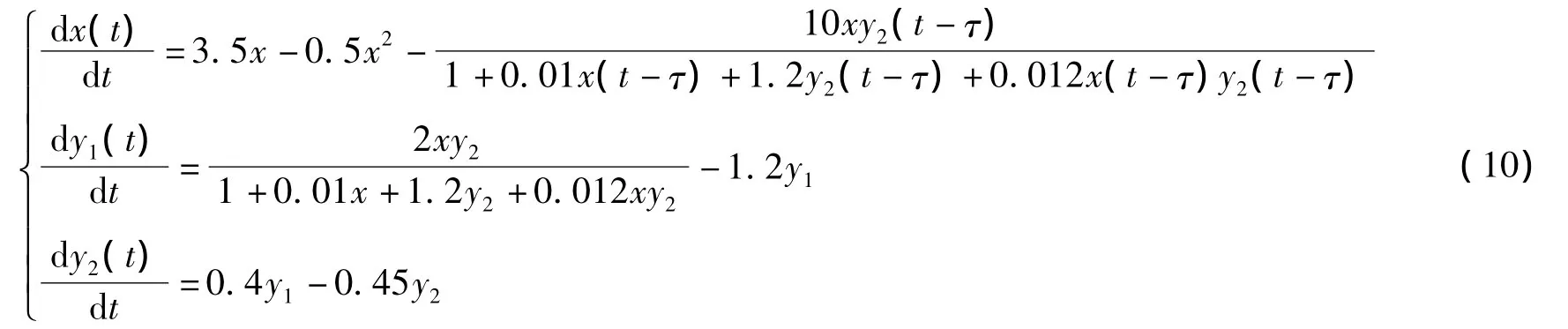
显然，a1－ar=0.465 0＞0，即系统(10)满足条件(H1):a1－ar≥0。系统(10)存在唯一正平衡点E*(1.065 8，0.527 1，0.468 5)。经过计算得到 ω0=2.701 5，τ0=0.536 6，λ′(τ0)=1.009 2 －0.307 0 i。根据定理1.1 可知，当 τ∈［0，0.536 6)时，系统(10)的正平衡点 E*(1.065 8，0.527 1，0.468 5)是渐近稳定的，如图1 所示。当 τ＞0.536 6 时，系统(10)的正平衡点 E*(1.065 8，0.527 1，0.468 5)是不稳定的，如图2所示。

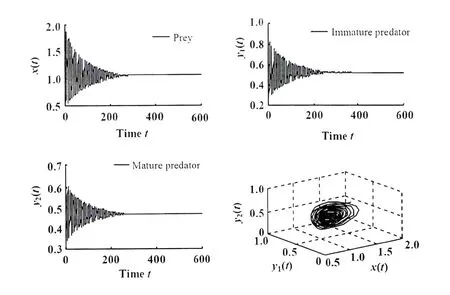
图1 初值为“1.545，0.487，0.685”，τ=0.495 ＜τ0=0.536 6时，E*渐近稳定

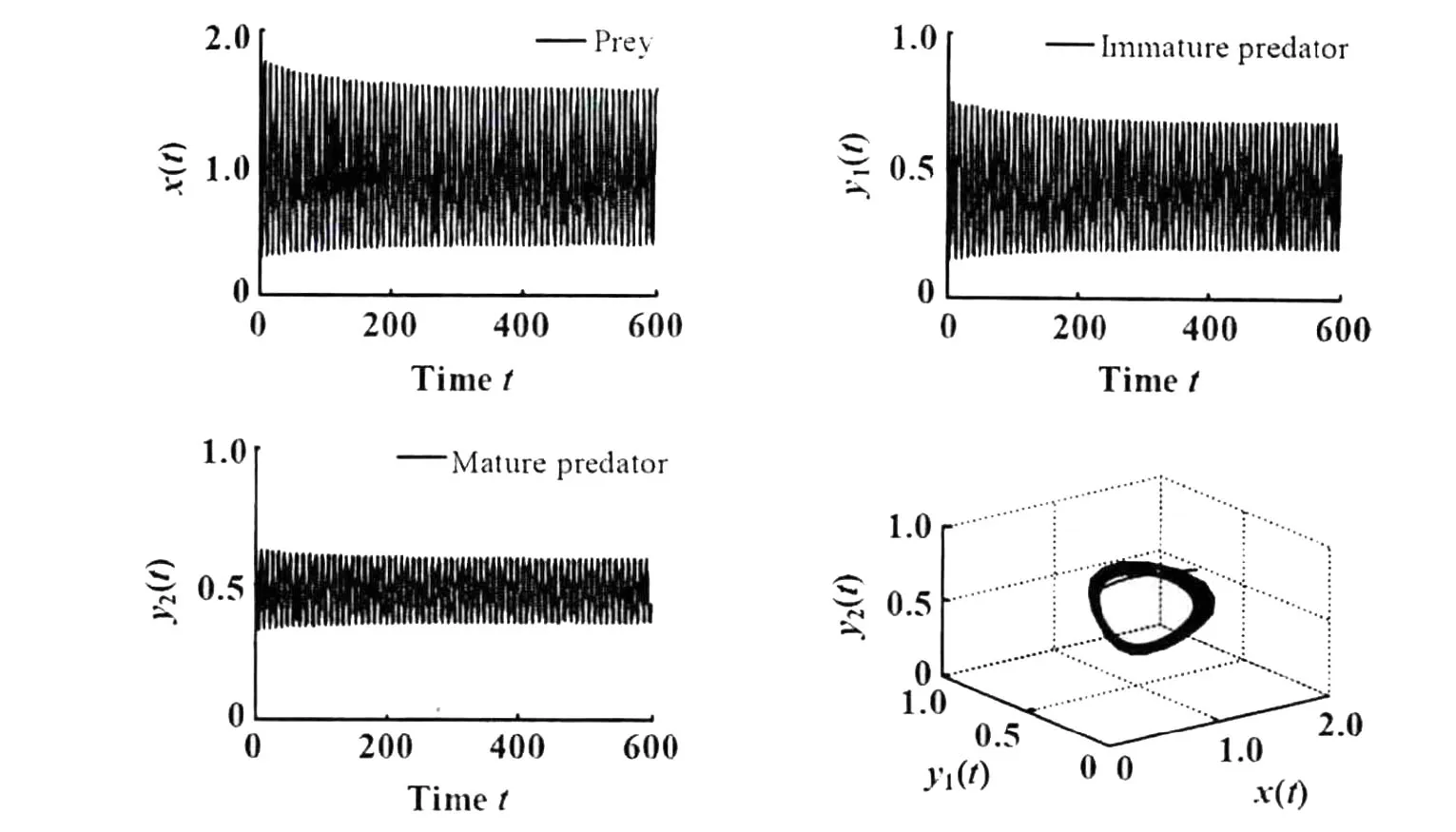
图2 初值为“1.545，0.487，0.685”，τ=0.575 ＜τ0=0.536 6时，E*是不稳定的

3 结 论

本次研究了一类捕食者具有阶段结构的时滞捕食系统模型。以成年捕食者的狩猎时滞为参数，分析了系统局部渐近稳定和局部Hopf分支的存在性。结果表明，当成年捕食者的狩猎时滞足够小(τ∈［0，τ0))，系统是局部渐近稳定的。一旦成年捕食者的狩猎时滞超越临界值τ0，系统将失去稳定性，并在临界值τ0处产生Hopf分支周期解。对于分支周期解的性质，有待进一步研究。

［1］ GAO Yong-fei，XIA Yong-hui.Periodic solutions of a nonautonmous plant-hare model［J］.浙江大学学报:理学版，2012，39(5):507-511.

［2］ HU Guang-ping，LI Xiao-ling.Stability and Hopf bifurcation for a delayed predator-prey model with disease in the prey［J］.Chaos，Solitons and Fractals，2012，45:229-237.

［3］ 刘娟，李医民.具有收获率的Holling III类生态系统的定性分析［J］.浙江大学学报:理学版，2012，39(3):249-252.

［4］ 秦桂毅，何德材，黄文韬.污染环境中一类捕食-食饵系统的持续性分析［J］.四川师范大学学报:自然科学版，2011，34(6):805-810.

［5］ BAEK Hunki.Species extinction and permanence of an impulsively controlled two-prey one-predator system with seasonal effects［J］.BioSystems，2009，98:7-18.

［6］ YANG Yu.Hopf bifurcation in a two-competitor，one-prey system with time delay［J］.Appl Math Comput，2009，214:228-235.

［7］ ZHANG Lai，LIN Zhi-gui.A Holling’s type II prey-predator model with stage structure and nonlocal delay［J］.Appl Math Comput，2011，217:5 000-5 010.

［8］ 张少林，朱婉珍.具有阶段结构的连续时滞生态系统的一致生存与全局渐近稳定性［J］.浙江大学学报:理学版，2006，33(4):376-378，392.

［9］ SHI Xiang-yun，ZHOU Xue-yong，SONG Xin-yu.Analysis of a stage-structured predator-prey model with Crowley-Martin function［J］.J Appl Math Comput，2011，36:459-472.

［10］ GE Zhi-hao，YAN Jing-jing.Hopf bifurcation of a predator-prey system with stage structure and harvesting［J］.Nonlinear Analysis:Theory，Methods and Applications，2011，74:652-660.

［11］ 王玲书.一类具有时滞和阶段结构的捕食者-食饵系统的全局稳定性［J］.高校应用数学学报，2013，28(1):51-62.

［12］ 耿春梅，林支桂.一类具有阶段结构的捕食系统的全局渐进稳定性［J］.淮阴师范学院学报:自然科学版:2007，6(3):179-186.

［13］ 袁媛，段复建.一类食饵具有阶段结构的时滞捕食系统的全局稳定性与Hopf分支［J］.云南大学学报:自然科学版，2013，35(1):13-20.

(责任编辑:朱宝昌)