余弦波形不平度激励下车架响应有限元计算

长春理工大学机电工程学院 刘宁

余弦波形不平度激励下车架响应有限元计算

长春理工大学机电工程学院 刘宁

本文对崎岖山区道路的路面不平度进行了抽象，以余弦波形作为车架的不平度作为输入激励，在利用ANSYS软件构建了某一型号车架的有限元模型基础上，对车架进行了模态分析，得到了车架的固有频率和振型，为车架抗耦合提供了理论支撑；并利用模态分析结果，将抽象后的余弦波形不平度作为路面激励进行了车架响应计算，得出了车架动态响应，包括车架应力随频率的关系和车架位移随频率的关系。

余弦波形；不平度激励；模态分析；有限元

在崎岖山区道路上行车的特点是道路条件差、车辆行驶速度较慢、路面不平度大等，其行车路面往往道路狭窄、曲折，而且凹凸不平。[1]在这样恶劣的行车条件下，车辆的车架强度及在动态激励作用下结构的动态响应成为车辆设计人员主要考虑因素。本文以某型号车辆的车架为分析对象，对崎岖山区道路的路面不平度以余弦波形简化抽象，计算了车架在此激励下的响应。

1 路面不平度简化抽象

在有限元计算中，对路面不平度的激励有功率谱算法和近似算法。功率谱算法需要预先知道路面的激励功率谱量值，而实际道路情况复杂，对不同路段会有不同量值，因此本文对路面不平度抽象成余弦波形，作为路面不平度激励。[2]

本文对凹凸不平的路面进行如下简化：假定路面每个凹凸波谷与波峰相等，且由波峰到波谷之间满足余弦函数，则就可以对崎岖路面简化如下，如图1.1所示：

图1 .1路面不平度波形图

图中1为波长；h为最高路面最高凹凸峰值；v为车辆的行驶速度。

式中2πv/1为波形频率。

以车辆减振弹簧为限，构建车辆振动模拟模型：将其划分为簧上弹簧—质量模型和簧下弹簧—质量模型，其示意图为图1.2所示：

图1 .2车辆振动模型示意图

其中m1，m2为簧下、簧上质量；k1，k2为轮胎刚度、悬架刚度；x为位移。

2 车架模型描述

车架在该车辆结构中，起到承载及连接作用，对车辆的油箱、驾驶室等进行承载，同时又连接车辆的上装部分使车桥、悬挂通过车架再与底盘上“正车架”相连。该车架采用16MnL材料，其材料模型参数为：弹性模量为210GPa，柏松比为0.3，抗拉强度为510MPa，屈服强度为345MPa。[3]

在ANSYS软件中建立该车架的几何模型，并采用SOLID95单元离散车架模型以构成车架有限元模型，离散后，该型车架的单元数量为235782个，节点数41866个，

其有限元模型如图2.1所示：

图2 .1该型车辆车架有限元模型

3 车架模态分析

由于车架在工作状态下，会有振动的激励，这些激励的频率有些是周期的，如发动机振动；有些频率是非周期的，如地面随机振动。模态分析作为结构动态分析的基础，除了提供车架的固有频率和振型外，还将作为其他动力学分析的起点。[4]

式（3.4）即为结构的自由振动频率方程，该方程为关于ω2的n次实系数方程。

从式（3.4）中解出ω2的n个实根i=1,2,…,n），便得到结构的第i阶固有频率，再将代入式（3.3）中，求解出矢量｝，即为结构第i阶的主振型。

对车架进行模态分析，采用兰索分块法提取分析结果，由于模态分析阶次越大，对振动耦合贡献越小，所以本文列出车架前10阶分析结果，第一阶为车架横振，具体模态固有频率如表3.1所示：

表3 .1 具体模态固有频率

限于篇幅，不列出振型图。从模态分析结果来看，整个模态频率较低，因此在当有低频激励下，容易与车架产生振动耦合；另外，车架的第4阶到第6阶频率很接近，在设计装配相配部件时，需要避开该区间。

4 车架不平度激励计算

设车辆在崎岖道路的行驶速度v=30m/s，不平度幅值h=30mm，波长l=1m。对该车辆车架进行路面不平度分析，采用有限元谐响应方法进行计算，得到其响应。本文选取车架上这样几个具有代表性的节点的响应结果：应力最大点、振幅最大点、发动机安装位置选取一节点，这三点的应力随频率的关系曲线如图4.1所示。

从该点的应力—频率关系可以看出，车架结构在频率为38Hz左右达到第一阶应力耦合点，该处应力最大可达到220MPa，在后续90Hz左右也会发生应力阶跃，但对结构影响比在38Hz时小得多。

图4 .2位移最大点的应力—频率关系图

在该点上，结构在36Hz左右，达到应力最大，其最大值为50MPa，该频率的应力同样基本为阶跃应力。

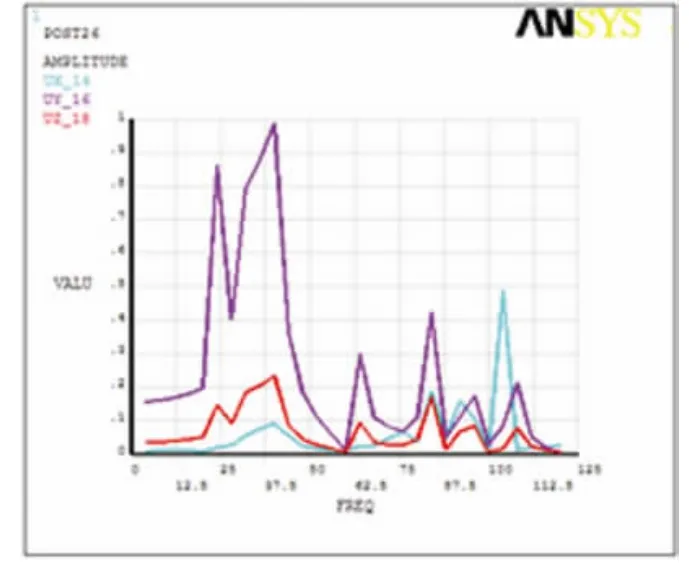
图4 .3位移最大点的位移—频率关系图

从位移与频率的关系图上来看，结构也在38Hz左右，达到位移振幅最大，其Y方向最大为9.8mm（本文中Y方向即竖直向上方向），这种共振振幅几乎是由载荷所引起振幅的两倍。

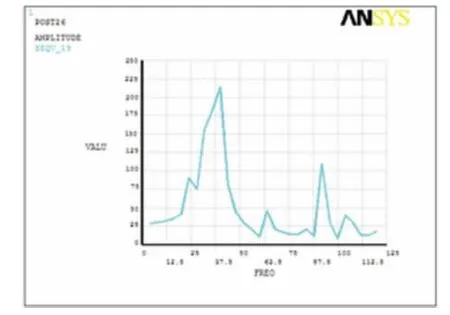
图4 .1应力最大点的应力—频率关系图

图4 .4发动机安装位置应力—频率关系

在发动机安装位置处，应力最大值同样是发生频率为38Hz左右时，在后面频率位置上，特别是在90Hz～110Hz之间，应力随频率的波动很大。

4 结论

本文将车辆中主要承载及起连接作用的车架作为分析对象，在ANSYS中建立了有限元模型，并对其进行了结构模态分析和路面不平度谐响应动态分析，其计算结果为：

（1）通过结构模态分析，车架第一阶固有频率较低，而且在第4阶到第6阶频率很接近，在设计装配相配部件时，需要避开固有频率带，以免发生共振耦合。

（2）通过对车架不平度计算，车架发生最大应力在38Hz左右，在该频率上，都可使应力与位移几乎扩大两倍，而且在后面的频率带，应力与位移都会随着固有频率产生较大的阶跃。

[1]肖生发，赵树朋.汽车构造[M].北京：北京大学出版社，2006，349-352

[2]Kim, G.H,Cho,K.z., Chyun,I.B.,hoi,G.S. Dynamic Stress Analysis of Vehicle Frame Using a nonlinear Finite Element Method. KSME International Journal, 2003,17（10）:1450-1457

[3]成大先主编.王德夫，姬奎生，韩学铨等副主编.机械设计手册[M].化学工业出版社，2008.04

[4]黄艾香，周天孝.有限元理论与方法[M].科学出版社，2009

[5]伍义生，吴永礼.有限元方法基础教程[M].电子工业出版社，2003

刘宁，男，1986年出生，硕士研究生，安徽人，研究方向：在线检测与装备。